Частные производные высших порядков - Методы решения системы линейных уравнений
Пусть z=f(x, y). Тогда и - частные производные по переменным х и у. В некоторых случаях существуют снова от этих функций частные производные, называемые частными производными второго порядка (или просто вторыми производными):
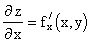
, ,
, и т. д.
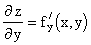
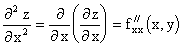
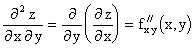
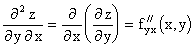
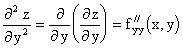
Можно определить частные производные любого порядка, если все рассматриваемые функции непрерывны как функции своих независимых переменных, при этом результат частного дифференцирования не зависит от последовательности дифференцирования.
Например, если и непрерывны, то имеет место равенство
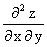
.
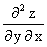
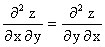
Пример. Пусть z = xY, ( x>0 ).
Имеем
; ;
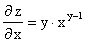
; .
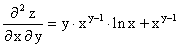
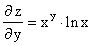
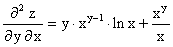
Признак полного дифференциала
Если u = f(x, y) - дифференцируема, то полный дифференциал имеет вид:
Du = P(x, y)dx + Q(x, y)dy, (14.10)
Где , .
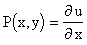
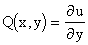
Возникает обратная задача: при каких условиях выражение
P(x, y)dx + Q(x, y)dy, (14.11)
Где функции P(x, y), Q(x, y) непрерывны со своими производными первого порядка, является полным дифференциалом функции u.
Теорема 14.1. (Необходимое условие)Для того, чтобы (14.11) являлось в некоторой области G полным дифференциалом некоторой функции u=F(x, y), необходимо, чтобы в этой области
(х, у О G)
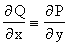
(*) - условие полного дифференциала.
Доказательство:
Пусть (14.11) - полный дифференциал функции u = F(x, y). Имеем
. (14.12)
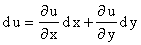
Отсюда в силу единственности дифференциала получим
, .
Дифференцируя первое по у, а второе - по х, будем иметь
, .
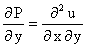
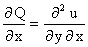
Но, так как для непрерывных функций результат дифференцирования не зависит от порядка дифференцирования, то получаем (*)
.
Следствие. Если условие (*) не выполнено, то выражение (14.4) не является полным дифференциалом.
Пример:
- А) ydx - xdy Б) ydx+xdy
Проверить, являются ли полными дифференциалами а) и б).
- А) , - не является. Б) P=y, Q=x,
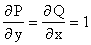
D(xy)=ydx+xdy.
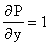
Основные понятия теории вероятности. Классическое определение вероятности
Статистическое определение вероятности. Классическое определение вероятности не является пригодным для изучения произвольных случайных событий. Так, оно неприемлемо, если результаты испытания не равновозможны. Например, при бросании неправильной игральной кости выпадение ее различных граней не равновозможно.
В таких случаях используется так называемое статистическое определение вероятности.
Пусть произведено n испытаний, при этом некоторое событие А наступило m раз.
Определение 1. Число m называется абсолютной частотой (или просто частотой) события А, а отношение Р*(А) = m/n называется относительной частотой события А.
Результаты многочисленных опытов и наблюдений помогают заключить: при проведении серий из n испытаний, когда число n сравнительно мало, относительная частота Р*(А) принимает значения, которые могут довольно сильно отличаться друг от друга. Но с увеличением n - числа испытаний в сериях - относительная частота Р*(А) = m/n приближается к некоторому числа Р(А), стабилизируясь возле него и принимая все более устойчивые значения.
Определение 2 (статистическое определение вероятности). Вероятностью события А в данном испытании называется число Р(А), около которого группируются значения относительной частоты при больших n.
Таким образом, относительная частота события приближенно совпадает с его вероятностью в статистическом смысле, если число испытаний достаточно велико (имеется огромный опытный материал по проверке последнего утверждения).
С этой точки зрения величина m = n Р(А) представляет собой среднее значение числа появления события А при n испытаниях.
Статистическое определение вероятности, использующее статистическую обработку данных, находит широкое применение.
При широких предположениях доказывается, что вероятности события в классическом и статистическом смыслах совпадают между собой.
Можно ли как-то измерить возможность появления некоторого случайного собы-тия? Другими словами, можно ли охарактеризовать эту воз-можность некоторым числом?
Всякое испытание влечет за собой некоторую совокупность исходов -- результатов испытания, т. е. событий. Во многих случаях возможно перечислить все события, которые могут быть исходами данного испытания.
Определение 1. Говорят, что совокупность событий образует полную группу событий для данного испытания, если его результатом обязательно становится хотя бы одно из них.
Определение 2. События U1, U2, ..., U, образующие полную группу попарно несовместимых и равновозможных событий, будем называть элементарными событиями.
Определение 3. Событие А называется благоприятствующим событию Б, если наступление события А влечет за собой наступление события В.
Определение 4 (классическое определение вероятности). Вероятностью Р(А) события А называется отношение m/n числа элементарных событий, благоприятствующих событию А, к числу всех элементарных событий, т. е. Р(А) = m/n.
Из приведенного классического определения вероятности вытекают следующие ее свойства.
1. Вероятность достоверного события равна единице.
Действительно, достоверному событию должны благоприятствовать все n элементарных событий, т. е. m = n, и, следовательно,
- 2. Вероятность невозможного события равна нулю. В самом деле, невозможному событию не может благоприятствовать ни одно из элементарных событий, т. е. m = 0, откуда 3. Вероятность случайного события есть положительное число, заключенное между нулем и единицей.
Похожие статьи
-
Счетные и несчетные множества - Методы решения системы линейных уравнений
Пусть, например, А и В Ї некоторые множества. Тогда их возможные взаимоотношения можно рассмотреть в виде таблицы: Диаграмма Венна Диаграмма Венна...
-
Элементы матричного анализа - Методы решения системы линейных уравнений
Вектором, как на плоскости, так и в пространстве, называется направленный Отрезок , то есть такой Отрезок , один из концов которого выделен и называется...
-
Пусть u = f(x, y) - функция, определенная в области w. Рассмотрим точку М(х, у) О w и некоторое направление l, определяемое направляющими косинусами Cosa...
-
Производной. - Методы решения системы линейных уравнений
Наиболее просто основные теоремы дифференциального исчисления формулируются для гладких функций. [ Править ] Производные и гладкие функции Пусть функция...
-
Ранг матрицы. - Методы решения системы линейных уравнений
Как было сказано Выше , минором матрицы порядка s называется определитель матрицы, образованной из элементов исходной матрицы, находящихся на пересечении...
-
Элементарные преобразования, Миноры - Методы решения системы линейных уравнений
Определение. Элементарными преобразованиями матрицы назовем следующие преобразования: 1) умножение строки на число, отличное от нуля; 2) прибавление к...
-
Определители (детерминанты) - Методы решения системы линейных уравнений
Определение. Определителем квадратной матрицы А= называется число, которое может быть вычислено по элементам матрицы по формуле: Det A = , где (1) М1к -...
-
Системы линейных уравнений - Методы решения системы линейных уравнений
Системой m линейных уравнений с n неизвестными называется система вида Где aIj и bI (i=1,...,m; b=1,...,n) - некоторые известные числа, а x1,...,xN -...
-
Функции и ее свойства - Методы решения системы линейных уравнений
В современной математике понятие множества является одним из основных. Универсальность этого понятия в том, что под него можно подвести любую...
-
Простейшие дроби и их интегрирование. - Методы решения системы линейных уравнений
Рациональной дробью называется дробь вида P(x)/Q(x), где P(x) и Q(x) - многочлены. Рациональная дробь называется правильной, если степень P(x) ниже...
-
Определение . Алгебраическим дополнением минора матрицы называется его Дополнительный минор , умноженный на (-1) в степени, равной сумме номеров строк и...
-
Свойства операции умножения матриц - Методы решения системы линейных уравнений
1)Умножение матриц не коммутативно, т. е. АВ ВА даже если определены оба произведения. Однако, если для каких - либо матриц соотношение АВ=ВА...
-
Матрицы и определители - Методы решения системы линейных уравнений
Определение. Матрицей размера mn, где m - число строк, n - число столбцов, называется таблица чисел, расположенных в определенном порядке. Эти числа...
-
Любая правильная рациональная дробь P(x)/Q(x) может быть единственным образом представлена в виде суммы простейших рациональных дробей. Для этого прежде...
-
Уравнение линии на плоскости - Методы решения системы линейных уравнений
Как известно, любая точка на плоскости определяется двумя координатами в какой - либо системе координат. Системы координат могут быть различными в...
-
Теорема 1. Предел постоянной равен самой постоянной. . Доказательство. f(x)=с, докажем, что . Возьмем произвольное e>0. В качестве d можно взять любое...
-
Сложение, вычитание, умножение комплексных чисел в алгебраической форме производят по правилам соответствующих действий над многочленами. Четность и...
-
ПРОИЗВОДНАЯ, ЕЕ СВОЙСТВА И ГЕОМЕТРИЧЕСКИЙ СМЫСЛ. ДИФФЕРЕНЦИАЛ. ПРОИЗВОДНАЯ ВЫСШИХ ПОРЯДКОВ Если отношение имеет предел при этот предел называют...
-
Основные формулы интегрирования (табличные интегралы) - Методы решения системы линейных уравнений
1. ?dx = x+C 2. ?xNDx = (xN+1/(n+1))+C (n?-1) 3. ?(dx/x) = ln(x)+C 4. ?aXDx = aXLn(a)+C 5. ?eXDx = eX +C 6. ?sin(x)dx = -...
-
Руководитель проекта сообщает тему и цель проекта, знакомит с исполнителями проекта. Акцентирует внимание учащихся на том, что проект носит обучающий...
-
Экономико-математические методы и моделирование в землеустройстве позволяют решать большой круг задач, связанных с оптимизацией территориальной...
-
При неизменности всех прочих факторов снижение цены ведет к соответствующему увеличению спроса и, наоборот, при прочих равных условиях увеличение цены...
-
Наша группа работала над учебным межпредметным проектом "Математические модели в рыночной экономике". Мы покажем применение в экономике систем уравнений....
-
1. Название проекта: "Математические модели в экономике". 2. Руководитель: учитель математики Тыкоцкая Л. И. 3. Учебные предметы: математика, экономика....
-
Логарифм числа b по основанию a (logAB) определяется как показатель степени, в которую надо возвести число a, чтобы получить число b (Логарифм существует...
-
Пусть функция определена в промежутке Х (рис.1). Исходя из некоторого значения независимой переменной, придадим ему приращение, не выводящее его из...
-
Пусть Dl, r() соответственно левые (правые) границы интервалов I, отвечающих на криволинейной трапеции ОИО значениям 0< < 1. Тогда интересующая нас...
-
Логарифм алгебраический угол число Формулы двойного аргумента Sin 2x=2sin xЧcos x Cos 2x=cosІx-sinІx Cos 2x=1-2sinІx Cos 2x=2cosІx-1 Обратные...
-
МАТРИЦЫ И ОПЕРАЦИИ НАД НИМИ Матрицей A называется любая прямоугольная таблица, составленная из чисел, которые называют элементами матрицы и обозначается...
-
В разделе 1 курсовой работы требуется: Определить количество закупаемого заданным филиалом фирмы сырья у каждого АО, (xj), максимизируя прибыль филиала....
-
Углом в один градус называется угол равный 1/180 части развернутого угла. Развернутый угол равен 180 градусам. Прямой угол равен половине развернутого...
-
Построим теперь на базе полиинтервальной оценки такую теоретико-вероятностную модель представления экспертных знаний, которая сочетала бы в себе описание...
-
РЕШЕНИЕ ЗАДАЧИ О КОММИВОЯЖЕРЕ МЕТОДОМ ВЕТВЕЙ И ГРАНИЦ: ОСНОВНАЯ СХЕМА - Задача коммивояжера
Пусть - конечное множество и - вещественно-значная функция на нем; требуется найти минимум этой функции и элемент множества, на котором этот минимум...
-
Ответ: уравнение ax2+bx+c=0. Где а не равно нулю, называется квадратным. Чтобы его решить нужно вычислить дискриминант. D=b2 -4ac и сравнить его с нулем....
-
Пусть требуется разыграть испытания в каждом из которых событие А появляется с вероятностью р и не появляется с вероятностью 1-р [4]. Заменим...
-
Решение систем линейных уравнений
Постановка задачи Решить Систему линейных уравнений при помощи метода Гаусса и через метод Крамера (вариант 82- 2) Теоретическая часть Матрица -- Таблица...
-
По продаже системного блока компьютера на базе процессора Celeron в одном из магазинов фирмы N за месяц сложилась следующая ситуация: Цена (тыс. рублей)...
-
Уравнение графический спрос равновесие С позиций воспитательного аспекта целью данного проекта является помощь учащимся в понимании жизненной...
-
Линейные уравнения и системы линейных уравнений над кольцом целостности - Евклидовость в математике
Математическое предположение, которое может быть только истинным, или ложным, "существует столбец значений неизвестных такой, что соответствующие этому...
-
Введение - Метод представления знаний в интеллектуальных системах поддержки экспертных решений
Во многих областях человеческой деятельности - науке, технике, бизнесе - широко распространены проблемные ситуации, которые могут быть описаны исходными...
Частные производные высших порядков - Методы решения системы линейных уравнений