Построение модели на реальных данных - Ранговый метод оценивания параметров регрессионной модели

Для построения линейной регрессионной модели на основе реальных данных при помощи рангового метода оценивания параметров был выбран достаточно известный набор данных "ирисы Фишера". Эти данные были собраны американским ботаником Эдгаром Андерсоном, они включают в себя измеренные в миллиметрах длину и ширину чашелистика и лепестка у 150 экземпляров цветка ириса - по 50 экземпляров каждого из трех видов: ирис щетинистый, ирис виргинский и ирис разноцветный.

В этой работе строится линейная регрессионная модель зависимости длины лепестка от длины и ширины чашелистика для вида ирис разноцветный. Такая модель имеет 2 регрессора и 50 наблюдений, для построения модели надо оценить при помощи рангового метода 3 параметра: свободный член и коэффициенты перед двумя регрессорами.

В результате запуска алгоритма, вычисляющего ранговую оценку параметров модели, получилось, что свободный член равен 0,3141, коэффициент перед длиной чашелистика равен 0,5429, а коэффициент перед шириной чашелистика равен 0,3571. На рисунках 4.1 и 4.2 представлены графики, изображающие построенную зависимость в виде плоскости и реальные наблюдения в виде кружков.

Так же для данной модели были построены МНК - и МНМ-оценки параметров. Затем в данные были внесены изменения: у одного случайно выбранного наблюдения значение зависимой переменной было увеличено в 10 раз - как в случае ошибки с порядком. Ранговая оценка, МНК - и МНМ-оценки параметров были пересчитаны, их изменение d2 было измерено вычислением суммы квадратов разностей соответствующих компонент старого и нового векторов для каждой оценки параметров. Результаты для наглядности представлены в таблице 4.1.

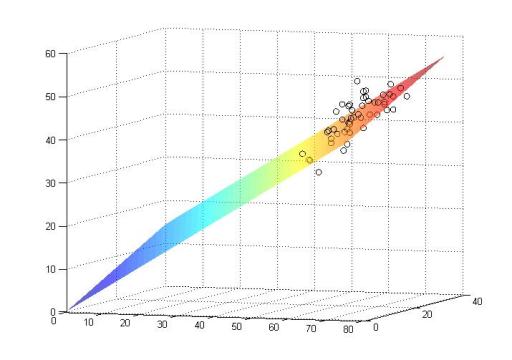
Рис. 4.1. График линейной регрессии и рассеивание данных

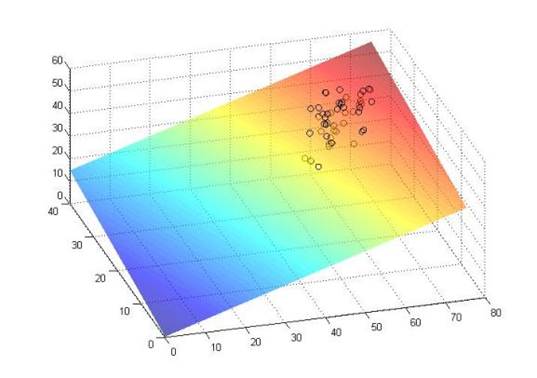
Рис. 4.2. График линейной регрессии и рассеивание данных

Таблица 4.1

Оценка:	Ранговая оценка	МНК-оценка	МНМ-оценка
Модель:	До изменений	После изменений	До изменений	После изменений	До изменений	После изменений
И0	0,3141	0,757	-1,1089	21,0407	0,9023	0,903
И1	0,5429	0,5899	0,578	1,5217	0,5574	0,5583
И2	0,3571	0,2446	0,3394	-2,3672	0,3108	0,3092
D2	0,211	498,8213	3,7607*10-6

Таким образом, можно сделать вывод, что наилучшим образом на выбросы в данных реагирует МНМ-оценка, наихудшим - МНК-оценка. Притом ранговая оценка показывает вполне удовлетворительные результаты.

На рисунке 4.3 изображен график линейной регрессии с ранговыми оценками параметров модели после внесения изменений в данные, на которых так же видно точку-выброс.

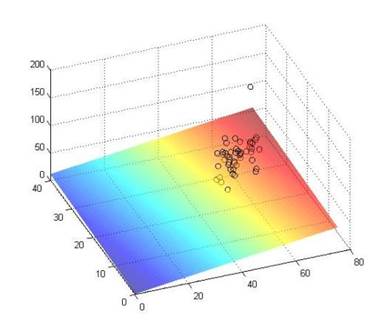
Рис. 4.3. График линейной регрессии после внесения изменений в данные

На рисунке 4.4 изображено изменение МНК-оценок параметров линейной регрессии в результате изменения данных: более бледная плоскость соответствует модели без внесенных выбросов, а более яркая - с выбросом.

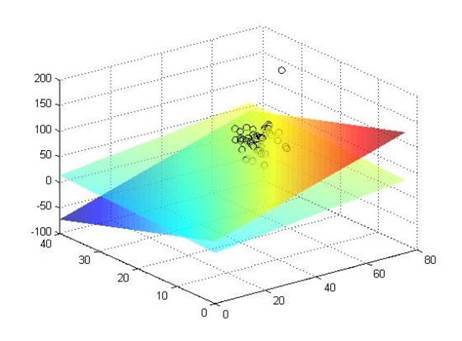
Рис. 4.4. Изменение МНК-оценок в результате изменения данных

В приложении № 4 представлен код для среды Matlab, при помощи которого была вычислена оценка параметров регрессии и построены графики, а так же проведен эксперимент на реальных данных.

В данной главе был рассмотрен пример применения рангового метода оценивания параметров линейной регрессионной модели к реальным данным и была построена линейная модель зависимости длины лепестка цветка ириса от длины и ширины его чашелистика. Так же было рассмотрено и сравнено влияние выбросов в данных на ранговую, МНК - и МНМ-оценки параметров модели с реальными данными.

Похожие статьи

• Заключение - Ранговый метод оценивания параметров регрессионной модели

  В данной работе был рассмотрен ранговый метод оценивания параметров регрессионной модели, был предложен способ приближенного вычисления ранговой оценки...

• Ранговый метод - Ранговый метод оценивания параметров регрессионной модели

  Метод наименьших квадратов широко применяется для оценки параметров линейной регрессии, поскольку достаточно прост в вычислении и при предположении о...

• Ранговый метод оценивания параметров регрессионной модели

  Пример кода, вычисляющий результаты эксперимента по сравнинию ранговой оценки, МНК - и МНМ-оценок параметров для модели с гауссовским распределением...

• Введение - Ранговый метод оценивания параметров регрессионной модели

  Объектом исследования в этой ВКР является ранговый метод оценивания параметров регрессионной модели. Этот метод применяется при построении регрессионных...

• Анализ информации о свойствах исследуемого изделия. Построение регрессионной модели по опытным данным

  Элементы корреляционного анализа Зависимость между случайными величинами (СВ) X и Y в теории вероятностей и математической статистике описывается, в...

• Асимптотическая относительная эффективность - Ранговый метод оценивания параметров регрессионной модели

  Вычисление АОЭ рангового метода по отношению к МНК и МНМ позволяет сделать выводы о том, какой метод лучше применять для оценки параметров в моделях с...

• Численный сравнительный анализ - Ранговый метод оценивания параметров регрессионной модели

  Итак, в рамках данной работы рассматриваются такие распределения случайных величин, как распределения Гаусса и Лапласа, треугольное распределение...

• Метод наименьших квадратов, Построение регрессионной прямой по сгруппированным данным - Моделирование в эконометрике

  Вычисляют выборочную дисперсию, характеризующую меру разброса опытных данных (x I ; Y I ) вокруг значений регрессии, то есть дисперсию остатков ....

• Построение модели с помощью метода деревьев решений - Моделирование вероятности банкротства

  В отличие от логистической регрессии, при использовании метода деревьев решений ограничения для независимых переменных отсутствуют, поэтому для...

• Методы оценки параметров структурной формы модели - Основы эконометрики

  Коэффициенты структурной модели могут быть оценены разными способами в зависимости от вида системы одновременных уравнений. Наибольшее распространение в...

• Подготовка данных для построения модели и статистический отбор объясняющих переменных - Уровень конкурентоспособности строительных компаний

  Для анализа был выбран временной диапазон с 2004 года по 2014 год. В целях построения прогнозной модели собранные годовые данные были разделены на две...

• Оптимизация, Верификация модели - Синтез скоринговой модели методом системно-когнитивного анализа

  Оптимизируем полученную модель с помощью удаления признаков, по которым имеется недостаточно данных. За пороговое значение встреч признаков в модели...

• Проблемы линейных регрессионных моделей, Предпосылки метода наименьших квадратов (условия Гаусса-Маркова) - Моделирование в эконометрике

  1. Предпосылки метода наименьших квадратов. 2. Проблема мультиколлинеарности. 3. Гомоскедатичность и гетероскедатичность. Линейные регрессионные модели с...

• Обобщенные интервальные оценки исходных данных - Метод представления знаний в интеллектуальных системах поддержки экспертных решений

  Построим теперь на базе полиинтервальной оценки такую теоретико-вероятностную модель представления экспертных знаний, которая сочетала бы в себе описание...

• Нелинейные модели регрессии - Моделирование в эконометрике

  Нелинейные модели регрессии и их линеаризация. 1. Типы нелинейных моделей: 2. Нелинейные модели линейные по объясняющим переменным и их линеаризация. 3....

• Задание №5, Проверить ряд на наличие выбросов методом Ирвина, сгладить методом простой скользящее средней с интервалом сглаживания 3, методом экспоненциального сглаживания (а=0,1), представить результаты графически, определить для ряда трендовую модель в виде полинома первой степени (линейную модель), дайте точечный и интервальный прогноз на три шага вперед. - Математические модели в экономике

  Проверить ряд на наличие выбросов методом Ирвина, сгладить методом простой скользящее средней с интервалом сглаживания 3, методом экспоненциального...

• Построение модели бинарного выбора несколькими методами - Уровень конкурентоспособности строительных компаний

  Итак, модели, которые будут дальше анализироваться, и получены с помощью Первого метода - проведения теста для выделения наиболее дескриптивных...

• Статистический анализ регрессионной модели, Интерпретация результатов эксперимента - Основы научных исследований

  После проведения регрессионного анализа получается модель объекта исследований в виде некоторой функции. В простейшем случае линейной регрессии она имеет...

• Моделирование системы в условиях неопределенности - Модели и методы решения проблемы выбора в условиях неопределенности

  В большинстве реальных больших систем не обойтись без учета "состояний природы" -- воздействий Стохастического типа, случайных величин или случайных...

• Построение многофакторной корреляционно-регрессионной модели производительности труда

  Построение многофакторной корреляционно-регрессионной модели производительности труда Данная работа направлена на выявление факторов, от которых зависит...

• Введение - Построение и анализ эконометрической модели зависимости суммы выдаваемых кредитов физическим лицам от денежных доходов населения и ставки рефинансирования

  Современные экономические теории и исследования опираются в значительной степени на использование математических моделей и методов анализа. Постоянно...

• Оценка адекватности моделей методом факторно-плоскостного пространственного проецирования

  Оценка адекватности моделей методом факторно-плоскостного пространственного проецирования Современная автомобильная промышленность ставит перед...

• Введение - Синтез скоринговой модели методом системно-когнитивного анализа

  Кредитно-финансовая система является одной из важнейших структур рыночной экономики, так как от темпов ее развития напрямую зависят темпы развития...

• Индексный анализ, Полиномиальная регрессия, Построение регрессии, Коэффициенты эластичности, Стандартизованные коэффициенты, Парные коэффициенты корреляции, Частные коэффициенты корреляции, Множественный коэффициент корреляции, Коэффициент детерминации, Колеблемость признака, Сезонность, Доверительные интервалы для параметров регрессии - Динамика ВВП РФ, статистический анализ

  Применим аппарат. Результаты приведены ниже Таблица 6. индексный анализ Рисунок 4. График сглаженного признака Полиномиальная регрессия Приведем массив...

• Модели и моделирование - Экономико-математические методы

  Одним из основных методов научного познания является эксперимент, а самой распространенной его разновидностью - метод моделирования систем. В процессе...

• Построение регрессионной зависимости для полного (ПФЭ) и дробного (ДФЭ) факторного эксперимента и их анализ - Выполнение регрессионного и дисперсионного анализа

  Задание 4 Найти оценки коэффициентов регрессионной зависимости У=а 0 +а 1 *х 1 +а 2 *х 2 +а 12 *х 1 *х 2 ,и проверить регрессионную зависимость на...

• Методы прогнозирования в статистике населения - Система источников данных о населении

  Моделирование временного тренда среднегодовой численности занят Ого населения Санкт-Петербурга Приведем данные среднегодовой численности занятого...

• Введение - Построение экономических моделей

  Современные экономические теории и исследования опираются в значительной степени на использование математических моделей и методов анализа. Постоянно...

• Модель для идеальных условий - Методика и модели оптимизации входных параметров технологической цепи хлебопродуктового объединения

  Хлебопродуктовый кооперация производственный технологический Согласно классической модели Харриса, рассматривается непрерывное расходование запасов и...

• Построение модели предсказания банкротств c использованием искусственных нейронных сетей - Влияние значений финансовых коэффициентов на вероятность банкротства компании

  Искусственные нейронные сети (ИНС) рассматриваются исследователями как возможная альтернатива статистическим методам. Исследования, использующие ИНС, как...

• Структура интеллектуальных систем поддержки экспертных решений - Метод представления знаний в интеллектуальных системах поддержки экспертных решений

  Реализация интеллектуальных систем поддержки решений (ИСППР) в задачах оценки перспективности объектов природопользования на ранних стадиях их...

• По 10 предприятиям отрасли имеются следующие данные за месяц: - Статистические показатели производства

  Номер предприятия 1 2 3 4 5 6 7 8 9 10 Валовой доход, млрд р. 5 6 7 8 9 10 11 12 13 14 Фонд оплаты, млрд р. 1 3 5 6 5 8 10 14 13 15 Найдите уравнение...

• Общая характеристика эконометрического моделирования в маркетинговых исследованиях - Эконометрические модели маркетинговой деятельности на предприятии

  Постоянство механизмов. Одно из условий, на которое опирается эконометрическое моделирование, состоит в том, что функциональное соотношение не меняется в...

• Использование в экономических исследованиях методов регрессии и корреляции - Эконометрика как наука

  Начальным пунктом эконометрического анализа зависимостей обычно является оценка линейной зависимости переменных. Это объясняется простотой исследования...

• Методы построения решений по математическим моделям - Математическое моделирование в электромеханике

  Системы дифференциальных уравнений, полученные для конкретных ти-пов электрических машин, содержат в скрытом виде исчерпывающую инфор-мацию о всех...

• Построение математической модели оптимизации выпуска продукции торгового предприятия - Математические методы и модели в экономике

  Обозначим через х1, х2, х3, х4 и х5 - объемы производимой предприятием продукции 1-го, 2-го, 3-го, 4-го и 5-го вида соответственно. Из условия следует,...

• Построение регрессии, Дисперсионный анализ, Эластичность, Доверительные интервалы для оцененных параметров - Статистика торговли автотранспортными средствами

  Для регрессии вида Найдем коэффициенты по формулам Вычислим Тогда Откуда Тогда линейная регрессия будет иметь вид Смысл коэффициента beta заключается в...

• Нахождение кратчайшего пути в транспортной сети - Применение экономико-математических методов и моделей в управлении производством (на примере КУП "Спецкоммунтранс")

  В зависимости от содержания задачи может быть два случая: когда ребра графа G единичной длины; когда ребра графа произвольной длины. Для каждого из этих...

• Модель БЭТ - Анализ удельной поверхности активированного угля, основанный на использовании метода тепловой десорбции газа-адсорбата (азота) с поверхности в динамических условиях с помощью специального адсорбера, прибора для текстурных измерений "Термосорб" серии М

  Знаменитая теория полимолекулярной адсорбции Брунауэра, Эммета и Теллера, получившая название теории БЭТ (по первым буквам фамилий ученых), основана на...

• Введение, Условия риска и неопределенности - Модели и методы решения проблемы выбора в условиях неопределенности

  Неопределенность - это фундаментальное свойство природы, а еще более (и точнее) - свойство, характеризующее неточность, незамкнутость, неокончательность,...

Построение модели на реальных данных - Ранговый метод оценивания параметров регрессионной модели

Предыдущая | Следующая