Асимптотическая относительная эффективность - Ранговый метод оценивания параметров регрессионной модели
Вычисление АОЭ рангового метода по отношению к МНК и МНМ позволяет сделать выводы о том, какой метод лучше применять для оценки параметров в моделях с большим объемом выборки.
Согласно Т. Хеттманспергеру Т. Хеттманспергер "Статистические выводы, основанные на рангах", М.: Финансы и статистика,1987, с. 249, АОЭ одного метода по отношению к другому определяется как корень степени p обратного отношения обобщенных дисперсий оценок параметров, полученных этими методами. Под обобщенной дисперсией вектора оценок параметров понимается определитель матрицы ковариаций оценок параметров, p - число параметров в модели. Если полученное число меньше единицы, то альтернативный метод эффективнее. Иначе более эффективным считается данный метод.
Ковариационная матрица МНК-оценки, согласно Дж. Себеру Дж. Себер "Линейный регрессионный анализ", М.: Мир, 1980, с.54, имеет вид
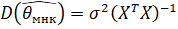
,
Где X - матрица плана, а у2 - дисперсия шумов модели. В случае, когда предполагается, что вектор шумов имеет гауссовское n-мерное распределение с нулевым математическим ожиданием и ковариационной матрицей у2 IN (диагональная, на диагонали - дисперсии у2), можно утверждать Дж. Себер "Линейный регрессионный анализ", М.: Мир, 1980, с.59, что вектор МНК-оценок параметров регрессии имеет гауссовское m-мерное распределение с математическим ожиданием и - вектором реальных значений параметров, и ковариационной матрицей.
В книге Т. Хеттманспергера Т. Хеттманспергер "Статистические выводы, основанные на рангах", М.: Финансы и статистика,1987, с. 247 приведена следующая теорема:
Пусть - любая точка, минимизирующая функцию D(Y-Xи). Тогда, если вектор и содержит истинные значения параметров и выполняются следующие предположения:
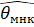
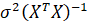
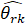
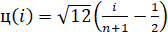
- - в функции D(Y-Xи) используются веса, - матрица [1X] (со столбцом из единиц) имеет полный столбцовый ранг, - матрица n-1[1X]T[1X] сходится к положительно определенной матрице, и матрица n-1XTX сходится к положительно определенной матрице У,
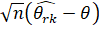
То вектор по распределению сходится к величине, имеющей m-мерное гауссовское распределение с нулевым математическим ожиданием и ковариационной матрицей
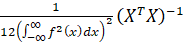
,
Где f(x) - плотность распределения шума.
В статье D. Pollard, Asymptotics for lest absolute deviation regression estimators, Econometric Theory, 7, 1991, p. 189 Д. Полларда приведена теорема о распределении МНМ-оценок параметров регрессионной модели:
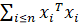
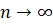
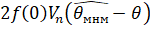
Пусть шумы еI независимы, одинаково распределены, с нулевой медианой и непрерывной, положительной функцией плотности f(.) в окрестности нуля. Пусть {xI} - детерминированная последовательность, для которой матрица имеет положительно определенный квадратный корень VN. Если при, то вектор имеет асимптотическое многомерное нормальное распределение с нулевым математическим ожиданием и единичной ковариационной матрицей.
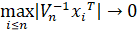
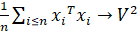
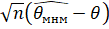
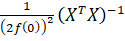
Условия на {xI} выполняются, если существует положительно определенная матрица V, такая что. Тогда вектор имеет m-мерное гауссовское распределение с нулевым математическим ожиданием и ковариационной матрицей.
Тогда АОЭ рангового метода по отношению к МНК выражается как
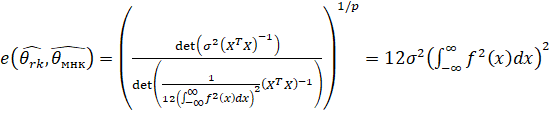
,
Где у2 - дисперсия шума, f(x) - плотность его распределения, p - число параметров модели.
АОЭ рангового метода по отношению к МНМ имеет вид
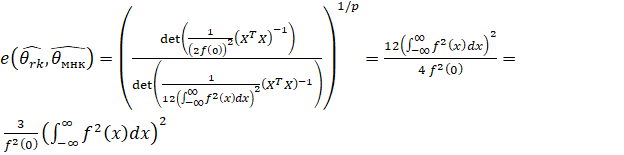
.
В таблице 3.1 приведены результаты вычислений АОЭ для различных распределений шумов регрессионной модели. Интегралы для распределений Стьюдента с различными степенями свободы, распределения Коши и логистического распределения были вычислены численно в среде Matlab, остальные были взяты аналитически.
Таблица 3.1
|
ОАЭ рангового метода к МНК |
ОАЭ рангового метода к МНМ | |
|
Нормальное распределение |
3/р ? 0,9549 |
1,5 |
|
Распределение Лапласа |
1,5 |
0,75 |
|
Распределение Коши |
? |
0,75 |
|
Распределение Стьюдента с 2 степенями свободы |
? |
1,0416 |
|
Распределение Стьюдента с 3 степенями свободы |
1,8998 |
1,1725 |
|
Распределение Стьюдента с 5 степенями свободы |
1,2412 |
1,3553 |
|
Распределение Стьюдента с 13 степенями свободы |
1,0252 |
1,4162 |
|
Распределение Стьюдента с 18 степенями свободы |
1,0023 |
1,438 |
|
Распределение Стьюдента с 19 степенями свободы |
0,9993 |
1,4417 |
|
Треугольное распределение |
8/9 ? 0,8889 |
4/3 ? 1,3333 |
|
Логистическое распределение |
Р2/9 ? 1,0966 |
4/3 ? 1,3333 |
|
Распределение Тьюки с г = 0,1, у12 = 100, у22 = 1 |
7,2804 |
1,267 |
Из полученных данных следуют такие выводы:
- - Ранговый метод уступает МНК в моделях с шумами, имеющими распределение Гаусса, Стьюдента с не менее чем 19 степенями свободы и треугольное распределение. - Ранговый метод уступает МНМ в моделях с шумами, имеющими распределения Лапласа и Коши.
Итак, в этой главе были рассмотрены и приведены результаты вычисления АОЭ рангового метода по отношению к МНК и МНМ. Так же были сделаны выводы об эффективности рангового метода по отношению к рассматриваемым альтернативным ему методам.
Похожие статьи
-
Заключение - Ранговый метод оценивания параметров регрессионной модели
В данной работе был рассмотрен ранговый метод оценивания параметров регрессионной модели, был предложен способ приближенного вычисления ранговой оценки...
-
Численный сравнительный анализ - Ранговый метод оценивания параметров регрессионной модели
Итак, в рамках данной работы рассматриваются такие распределения случайных величин, как распределения Гаусса и Лапласа, треугольное распределение...
-
Ранговый метод - Ранговый метод оценивания параметров регрессионной модели
Метод наименьших квадратов широко применяется для оценки параметров линейной регрессии, поскольку достаточно прост в вычислении и при предположении о...
-
Введение - Ранговый метод оценивания параметров регрессионной модели
Объектом исследования в этой ВКР является ранговый метод оценивания параметров регрессионной модели. Этот метод применяется при построении регрессионных...
-
Построение модели на реальных данных - Ранговый метод оценивания параметров регрессионной модели
Для построения линейной регрессионной модели на основе реальных данных при помощи рангового метода оценивания параметров был выбран достаточно известный...
-
Ранговый метод оценивания параметров регрессионной модели
Пример кода, вычисляющий результаты эксперимента по сравнинию ранговой оценки, МНК - и МНМ-оценок параметров для модели с гауссовским распределением...
-
Методы оценки параметров структурной формы модели - Основы эконометрики
Коэффициенты структурной модели могут быть оценены разными способами в зависимости от вида системы одновременных уравнений. Наибольшее распространение в...
-
Аналитические модели, записывающиеся в виде математических конструкций, не включающих логических условий, приводящих к разветвлению вычислительного...
-
Основные понятия теории экономико-математического моделирования Кибернетический подход к исследованию экономико-математических систем Обычно...
-
Составляется матрица численных значений базисных функций, соответствующая расширенной матрице спектра плана Вычисляется информационная матрица...
-
Для достижения поставленной цели предприятию требуются материалы, оборудование, энергия, рабочая сила и другие ресурсы. Каждое предприятие такими...
-
Оценка адекватности моделей методом факторно-плоскостного пространственного проецирования
Оценка адекватности моделей методом факторно-плоскостного пространственного проецирования Современная автомобильная промышленность ставит перед...
-
Охарактеризовать виды моделей - Методы линейного программирования
Модель -- это некий новый объект, который отражает существенные особенности изучаемого объекта, явления или процесса. Один и тот же объект может иметь...
-
1. Предпосылки метода наименьших квадратов. 2. Проблема мультиколлинеарности. 3. Гомоскедатичность и гетероскедатичность. Линейные регрессионные модели с...
-
Пусть Dl, r() соответственно левые (правые) границы интервалов I, отвечающих на криволинейной трапеции ОИО значениям 0< < 1. Тогда интересующая нас...
-
Модели теории игр. Основные определения и термины В разных областях целенаправленной деятельности, например при разработке и эксплуатации АСУ, часто...
-
В большинстве реальных больших систем не обойтись без учета "состояний природы" -- воздействий Стохастического типа, случайных величин или случайных...
-
Важной задачей статистики является разработка методики статистической оценки социально-экономических явлений, которая осложняется тем, что многие...
-
Коэффициенты структурной модели могут быть оценены разными способами в зависимости от вида системы одновременных уравнений. Наибольшее распространение...
-
Методы исследования математических моделей - Математическое моделирование в менеджменте и маркетинге
Все методы математического моделирования можно разделить на четыре класса: -аналитические (априорные); -имитационные (априорно-апостериорные) модели;...
-
Проверить ряд на наличие выбросов методом Ирвина, сгладить методом простой скользящее средней с интервалом сглаживания 3, методом экспоненциального...
-
Заключение, Список литературы - История развития методов и моделей в экономике
Разработка математических методов и моделей оптимизации отдельных производственно-экономических процессов, общественного производства в целом, оказалось...
-
Введение - Синтез скоринговой модели методом системно-когнитивного анализа
Кредитно-финансовая система является одной из важнейших структур рыночной экономики, так как от темпов ее развития напрямую зависят темпы развития...
-
Подход к постановке задачи аналогичен предыдущему, но в качестве исходной модели рассматривается матрица инциденций Q = [ Q (i, j)]. Столбцам матрицы...
-
Классификация экономико-математических методов - История развития методов и моделей в экономике
Велика роль математических моделей при описании экономических объектов и процессов, что, безусловно, подтверждается историей развития этого направления...
-
Введены понятия приведенных (к процессам преобразования) удельных затрат в звеньях технологической цепи. Разработана математическая модель для оценки...
-
Имеется выборка объема n экспериментальных значений. Предполагаем, что ошибки вычисления пренебрежимо малы, а случайные ошибки измерения температур...
-
Методы наименьших квадратов - Системы эконометрических уравнений, их применение в эконометрике
Как уже отмечалось, разработана масса методов эвристического анализа систем эконометрических уравнений. Они предназначены для решения тех или иных...
-
При невыполнимости предпосылки постоянства дисперсий отклонений гомоскедастичность) последствия применения МНК будут следующими. 1. Оценки коэффициентов...
-
Метод максимального правдоподобия - Основы научных исследований
Разработан Р. Фишером. Пусть Х 1 ,х 2 ...х N - выборка из генеральной совокупности случайной величины Х с функцией плотности вероятности Р(х, и),...
-
Основные понятия сетевых и графовых моделей Объектом исследования является сеть, состоящая из узлов и линий связи. Предполагается, что в сети имеется два...
-
Классификация экономико-математических моделей Математические модели экономических процессов и явлений более кратко можно назвать...
-
Используется адаптивная нейро-нечеткая система вывода ANFIS, функционально эквивалентная системе нечеткого вывода Сугено. Вывод осуществляется за два...
-
Из перечисленного обзора типов ММ, составляющих предмет ИСО, можно выделить следующие особенности ММ ИСО [3]. - Системный подход, заставляющий...
-
После проведения регрессионного анализа получается модель объекта исследований в виде некоторой функции. В простейшем случае линейной регрессии она имеет...
-
Знаменитая теория полимолекулярной адсорбции Брунауэра, Эммета и Теллера, получившая название теории БЭТ (по первым буквам фамилий ученых), основана на...
-
Методы измерения параметров тренда - Ряды динамики в статистике
Тенденция ряда динамики (тренд). Важнейшим направлением в исследовании закономерностей динамики социально-экономических процессов является изучение общей...
-
При управлении подвижными объектами (такими, например, как мобильные роботы, подводные аппараты и т. п.) часто имеет место неопределенность цели, когда...
-
В большинстве случаев структурная неопределенность вызвана неполнотой знания аналитической структуры уравнений модели объекта управления. При не...
-
Модели и моделирование - Экономико-математические методы
Одним из основных методов научного познания является эксперимент, а самой распространенной его разновидностью - метод моделирования систем. В процессе...
Асимптотическая относительная эффективность - Ранговый метод оценивания параметров регрессионной модели