Общее решение, Общее решение в орбитальных координатах - Математическое моделирование движения небесных тел
Общее решение задачи двух тел можно получить из общего интеграла, представляющего собой не что иное, как неявную форму задания общего решения.
Общее решение в орбитальных координатах
В этом разделе рассматривается движение тела M в орбитальных прямоугольной M0??? и цилиндрической M0rv? системах координат. Положение орбитальной системы координат в пространстве определяется тремя кеплеровскими элементами ?,i,?. Долгота восходящего узла ? и
Наклонение i определяют положение плоскости орбиты M0??, а аргумент перицентра ? определяет положение оси M0? в плоскости орбиты. При переходе от относительной системы M0xyz к орбитальной системе M0??? кеплеровские элементы ?,i,? считаются известными. Поэтому общее решение в орбитальной системе координат зависит только от трех оставшихся кеплеровских элементов p, e,?, которые можно рассматривать как произвольные постоянные. Это отражено в последующей формуле, в которой фокальный параметр p, эксцентриситет e и время прохождения через перицентр ? входят в общее решение для орбитальной системы ?, ?, ??, ??, ?=0, ??=0, а элементы ?,i,? появляются только при переходе к относительной системе координат посредством направляющих косинусов ??,??,??,?!,?',?'.
Задача определения общего решения в орбитальных координатах сводится к получению зависимостей:
?, ?, ??, ??
R, v, r?, v?
t, p, e.? ,- для прямоугольной системы M0??? ,
T, p, e, ? ,- для цилиндрической системы M0rv? , (1.23)
А аппликата ? и ее производная ?? тождественно равны нулю.
Уравнение орбиты в полярных координатах связывает переменные r и v. Для вывода зависимости величин r и v от времени рассмотрим интеграл площадей в цилиндрической системе координат. Сначала при c1=c2=0 и c3=c с учетом ?=??=0 запишем интеграл площадей в орбитальных декартовых координатах в виде
, (1.24)
А затем путем замены переменных
,
(1.25)
Из (1.23) получим интеграл площадей в цилиндрической системе координат M0rv?
, (1.26)
Где r определяется формулой (1.8).
Интегрируя это равенство, получим зависимость времени t от истинной аномалии v в виде
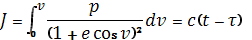
(1.27)
Где произвольная постоянная ? (момент прохождения через перицентр) соответствует значению истинной аномалии v=0. Это уравнение мы будем использовать в дальнейшем вместо интеграла, зависящего явно от времени.
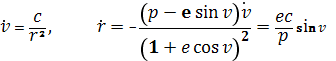
(1.28)
Подставляя полученные значения для v? и r? в выражения (1.25) для ?? и ?? и учитывая, что зависимость t от v задается формулой (1.27), получим общее решение в орбитальной цилиндрической системе координат
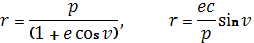
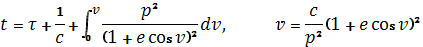
(1.29)
С учетом (1.29) общее решение в орбитальных прямоугольных координатах будет задаваться формулами (1.25) после обращения интеграла (1.27), т. е. получения зависимости истинной аномалии v от времени t.
Радиальная и трансверсальная компоненты скорости движения тела M представляются в виде
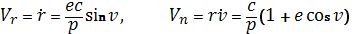
(1.30)
А сама скорость записывается в виде:
(1.31)
Похожие статьи
-
Параболическое движение, Прямолинейное движение - Математическое моделирование движения небесных тел
(p = 0, e = 1) Уравнение параболической орбиты записывают в видеp r = 1 + cos v (1.80) Где величина определяет расстояние от центра притяжения M0 до...
-
Общее решение уравнений относительного движения - Математическое моделирование движения небесных тел
Рассмотрим на небесной сфере сферический треугольник N M x, где M - проекция текущего положения тела M на небесную сферу. Сторонами этого треугольника...
-
Гиперболическое движение - Математическое моделирование движения небесных тел
(p=0,e>1) Каноническое уравнение гиперболы в центральных прямоугольных координатах O?!?! представляется в виде (1.68) Где a - действительная, а b...
-
Круговое движение, Эллиптическое движение - Математическое моделирование движения небесных тел
(p = 0, e = 0) Круговое движение представляет собой наиболее простой случай движения в задаче двух тел. Только для кругового движения (и прямолинейного...
-
Кеплеровские элементы орбиты - Математическое моделирование движения небесных тел
Вместо произвольных постоянных c1,c2,c3,h,?1,?2,?3,? в астрономии обычно используются более наглядные и более удобные постоянные...
-
Уравнение Бине - Математическое моделирование движения небесных тел
Другой способ получения траектории движения в задаче двух тел связан с широко известным уравнением Бине. Это уравнение записывается в цилиндрической...
-
Орбиту можно получить как линию пересечения двух поверхностей. Уравнение одной поверхности - это уравнение плоскости орбиты. Уравнение второй поверхности...
-
Результаты проведенного интегрирования позволяют Сформулировать два первых обобщенных закона Кеплера. Первый закон: невозмущенной орбитой является кривая...
-
Лунная поверхность места посадки моделируется как плоскость и импортируется в формат STL как дискретизованная поверхность. Модель космического аппарата...
-
Орбитальная система координат - Математическое моделирование движения небесных тел
Орбитальная система координат вводится следующим образом. Ось направим по вектору Лапласа ?, ось - по вектору c, а ось - перпендикулярно к этим осям...
-
Введение - Математическое моделирование движения небесных тел
В небесной механике для описания движений небесных тел в зависимости от конкретных условий используются различные физические модели - идеализированные...
-
Заключение - Математическое моделирование движения небесных тел
Небесная механика на протяжении всей истории ее становления была источником новых идей, методов и даже новых направлений в математике, традиционно...
-
Строение Солнечной системы - Законы движения небесных тел и строение Солнечной системы
Хорошо известно, что основная масса Солнечной системы (около 99.8%) приходится на ее единственную звезду - Солнце. Суммарная масса планет составляет...
-
Закон Всемирного тяготения - Законы движения небесных тел и строение Солнечной системы
Законы Кеплера прекрасно описывали наблюдаемое движение планет, но не вскрывали причин, приводящих к такому движению (напр. вполне можно было считать,...
-
Рассмотрим, наконец, общую схему вычисления возмущенных координат спутника. Элементы орбиты. Примем за основную систему произвольных постоянных теории...
-
4.1 Введение В предыдущих главах было подробно изучено промежуточное движение искусственного спутника. Была рассмотрена качественная картина движения,...
-
Эклиптическая система координат - Общие сведения о небесных сферах
Эклиптическая система координат, или эклиптикальные координаты -- это система небесных координат, в которой основной плоскостью является плоскость...
-
Экваториальная система координат Система координат, в которой отсчет производится от плоскости экватора, называется экваториальной. Угловое расстояние...
-
Введение - Аномальное движение орбит в общей теории относительности
Как известно, в общей теории относительности можно определить аномальное движение орбит [1]. Для решения задачи о вековом аномальном смещении перигелия...
-
Математическое описание модели Прямое солнечное излучение на модели КА рассчитывается аналогичным образом как для поверхности Луны, т. е. делая допущения...
-
Покажем, что для любой классической системы, обладающей центральной симметрией и заданной энергией, существует такая метрика, что действие системы будет...
-
"Движение" пробных тел. Что такое "движение" пробного тела? - Геометрия физического пространства
Конечно, это не перемещение подпространства, описывающего данное, пробное тело, в пространстве событий относительно подпространства пробного тела или...
-
Притяжение объемного тела - Движение искусственного спутника Земли в нецентральном поле тяготения
Рассмотрим задачу о притяжении материальной точки Р единичной массы некоторым телом М. Будем предполагать, что тело имеет произвольную форму, а плотность...
-
Двумя наиболее значительными успехами классического естествознания, основанного на механике Ньютона, были практически исчерпывающее описание наблюдаемого...
-
Сравнивая дуги, на которые перемещаются планеты за равные промежутки времени, установить, какая из планет быстрее движется на звездном небе, и объяснить...
-
Мы конкретизировали понятия, используемые в рассматриваемой области, но нужно еще указать характеристики телескопа, предпочтительные с точки зрения...
-
Исследование зависимости энергетики поддержания гало-орбиты от места и направления исполнения импульса Суммарный импульс, затрачиваемый на коррекции для...
-
При моделировании влияния расстояния до небесных тел на интегральную информативность было обнаружено, что наиболее достоверно зависимости выявляются в...
-
Вращение небесных сфер - Общие сведения о небесных сферах
В экваториальной системе координат главная ось - это ось мира, проходящая через полюса мира P и P' (рисунок 1.3), а главная плоскость - перпендикулярная...
-
Спектральный анализ небесных тел - Астрономия наших дней
Могучим оружием о исследовании Вселенной стал для астрономов спектральный анализ - изучение интенсивности излучения в отдельных спектральных линиях, в...
-
Для решения системы линейных уравнений (4.18) воспользуемся итерационным методом Гаусса-Зейделя. Перепишем (4.18) в матричном виде: (4.14) Матрица А...
-
Математическое описание модели Модель "Radiocity" Расчет излучения в результате переотражения элементами космического аппарата друг на друга выполнятся с...
-
Все малые тела Солнечной системы являются несамосветящимися, и они видны лишь благодаря рассеиванию ими падающего на них солнечного света. Вследствие...
-
-508-мм, светосилой 1:8, роботизированный телескоп системы Ричи- Кретьена, установленный на монтировке Парамаунт; 305-мм, светосилой 1:10, телескоп...
-
В этой части мы сведем дифференциальные уравнения (2.1.6) к квадратурам, которые и будут в дальнейшем использованы для построения промежуточной орбиты...
-
Работы над многоразовым орбитальным кораблем были начаты в 1974 году в рамках подготовки "Комплексной программы НПО "Энергия". Это направление работ было...
-
В предыдущих главах были выведены формулы, позволяющие вычислять положение спутника в пространстве для любого момента времени, если известны численные...
-
Математическая модель В данной работе, для описания движения КА, была использована вращающаяся система координат с фиксированным направлением...
-
Исследование случая неточного определения координат КА. - Космический аппарат
Рис. 33 Иллюстрирует эволюцию максимального отклонения от номинальной траектории при изменении начального положения аппарата. На рисунке представлены...
-
Нецентральность гравитационного поля Земли - Возмущенное движение космического аппарата
Возмущенный движение гравитационный орбита При решении ограниченной задачи двух тел Земля представляется шаром со сферическим распределением плотности. В...
Общее решение, Общее решение в орбитальных координатах - Математическое моделирование движения небесных тел