Моделирование траектории движения небесных тел, Уравнения орбиты в относительных координатах - Математическое моделирование движения небесных тел
Орбиту можно получить как линию пересечения двух поверхностей. Уравнение одной поверхности - это уравнение плоскости орбиты. Уравнение второй поверхности выведем далее с помощью векторного интеграла Лапласа.
Уравнения орбиты в относительных координатах
Умножение интеграла Лапласа скалярно на вектор
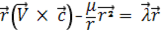
(1.1)
Позволяет получить соотношение, не содержащее скорость. Осуществляя циклическую перестановку в смешанном произведении векторов, уравнение (1.1) перепишем в виде
(1.2)
Это уравнение в трехмерном пространстве координат определяет некоторую поверхность. Учитывая, что уравнение (1.2) получено из интеграла Лапласа, указанную поверхность будем называть поверхностью Лапласа.
Траекторию движения тела тогда можно получить как пересечение поверхности Лапласа (1.2) с плоскостью орбиты и представить в виде системы двух уравнений
, (1.3)
В орбитальной системе координат, т. е. при,
, , уравнения орбиты преобразуются к виду
, . (1.4)
Из первого уравнения в (1.4) видно, что поверхность Лапласа (1.3) является осесимметричной поверхностью второго порядка. Чтобы дать более точную характеристику этой поверхности, а вместе с ней и орбиты, осуществим переход к сферической системе координат при помощи преобразования:
,, , (1.5)
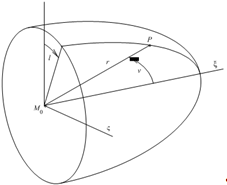
Рис. 1.1. Фрагмент поверхности Лапласа для.
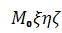
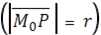
Точка иллюстрирует текущую точку поверхности в системах координат и соответственно, где l - долгота, отсчитываемая в плоскости от оси ? в положительном направлении, v - полярное расстояние, отсчитываемое от оси (т. е. от вектора ?). В любой плоскости, проходящей через ось, величину v можно рассматривать как полярный угол, отсчитываемый от полярной оси. Общий вид части поверхности Лапласа (для ) показан на рис. 1.1.
Используя формулы (1.6), из (1.5) получим уравнения орбиты в сферической системе координат в виде
,
. (1.6)
Так как долгота l не входит в первое уравнение системы (1.7) (уравнение поверхности Лапласа), то можно заключить, что эта поверхность является поверхностью вращения вокруг оси.
Преобразуем первое уравнение системы (1.7) путем разрешения его относительно r, а, исключая из рассмотрения прямолинейное движение (т. е. полагая c=0, r=0, v=0), второе уравнение (плоскости орбиты) представим в виде равенства l=0. Тогда систему (1.7) можно записать в виде
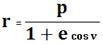
, l=0, (1.7)
Где введены обозначения
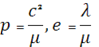
. (1.8)
Таким образом, траекторию в плоскости движения тела можно записать в виде фокального уравнения кривой второго порядка в полярных координатах (r, v) с полюсом M0, расположенным в одном из фокусов:
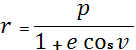
, (1.9)
Где p - фокальный параметр кривой, e - ее эксцентриситет, а v - полярный угол, отсчитываемый от фокальной оси.
Кривая (1.10) может быть эллипсом, параболой, гиперболой и их вырождениями - отрезками и лучами прямых. Вращением этой кривой вокруг полярной оси получается поверхность, которая может оказаться эллипсоидом вращения, параболоидом вращения, двуполостным гиперболоидом вращения, отрезком или лучом прямой.
Полярный угол v в уравнении орбиты отсчитывается от направления на ближайшую к телу точку кривой, которое задается вектором ?. Этот угол в астрономии называется истинной аномалией. Ближайшая точка орбиты называется перицентром, наиболее удаленная - апоцентром. Для реальных небесных тел используются конкретные названия: для Земли - перигей и апогей, для Солнца - перигелий и афелий, для Юпитера - перииовий и апоиовий, для Луны - периселений и апоселений, для звезды - периастр и апоастр, для Марса - перимарсий и апомарсий, для Венеры - перивенерий и аповенерий и т. п.
Фокальную ось называют также линией апсид орбиты, а точки ее пересечения с орбитой - апсидами. Апсиды совпадают с вершинами кривой второго порядка.
Похожие статьи
-
Гиперболическое движение - Математическое моделирование движения небесных тел
(p=0,e>1) Каноническое уравнение гиперболы в центральных прямоугольных координатах O?!?! представляется в виде (1.68) Где a - действительная, а b...
-
Круговое движение, Эллиптическое движение - Математическое моделирование движения небесных тел
(p = 0, e = 0) Круговое движение представляет собой наиболее простой случай движения в задаче двух тел. Только для кругового движения (и прямолинейного...
-
Уравнение Бине - Математическое моделирование движения небесных тел
Другой способ получения траектории движения в задаче двух тел связан с широко известным уравнением Бине. Это уравнение записывается в цилиндрической...
-
Общее решение задачи двух тел можно получить из общего интеграла, представляющего собой не что иное, как неявную форму задания общего решения. Общее...
-
Кеплеровские элементы орбиты - Математическое моделирование движения небесных тел
Вместо произвольных постоянных c1,c2,c3,h,?1,?2,?3,? в астрономии обычно используются более наглядные и более удобные постоянные...
-
Параболическое движение, Прямолинейное движение - Математическое моделирование движения небесных тел
(p = 0, e = 1) Уравнение параболической орбиты записывают в видеp r = 1 + cos v (1.80) Где величина определяет расстояние от центра притяжения M0 до...
-
Общее решение уравнений относительного движения - Математическое моделирование движения небесных тел
Рассмотрим на небесной сфере сферический треугольник N M x, где M - проекция текущего положения тела M на небесную сферу. Сторонами этого треугольника...
-
Введение - Математическое моделирование движения небесных тел
В небесной механике для описания движений небесных тел в зависимости от конкретных условий используются различные физические модели - идеализированные...
-
Лунная поверхность места посадки моделируется как плоскость и импортируется в формат STL как дискретизованная поверхность. Модель космического аппарата...
-
Орбитальная система координат - Математическое моделирование движения небесных тел
Орбитальная система координат вводится следующим образом. Ось направим по вектору Лапласа ?, ось - по вектору c, а ось - перпендикулярно к этим осям...
-
Результаты проведенного интегрирования позволяют Сформулировать два первых обобщенных закона Кеплера. Первый закон: невозмущенной орбитой является кривая...
-
Заключение - Математическое моделирование движения небесных тел
Небесная механика на протяжении всей истории ее становления была источником новых идей, методов и даже новых направлений в математике, традиционно...
-
Поскольку характеристики околоземной орбиты зависят от времени старта и космодрома, с которого осуществляется запуск, далеко не все комбинации...
-
Математическая модель В данной работе, для описания движения КА, была использована вращающаяся система координат с фиксированным направлением...
-
Все малые тела Солнечной системы являются несамосветящимися, и они видны лишь благодаря рассеиванию ими падающего на них солнечного света. Вследствие...
-
4.1 Введение В предыдущих главах было подробно изучено промежуточное движение искусственного спутника. Была рассмотрена качественная картина движения,...
-
Строение Солнечной системы - Законы движения небесных тел и строение Солнечной системы
Хорошо известно, что основная масса Солнечной системы (около 99.8%) приходится на ее единственную звезду - Солнце. Суммарная масса планет составляет...
-
2.1 Дифференциальные уравнения движения искусственного спутника Мы ввели подвижную, жестко связанную с Землей, систему координат и соответствующие ей...
-
В рамках данной работы производился расчет параметров отлетного вектора при заданных ограничениях на геометрию орбиты. С учетом заданных характеристик Az...
-
Для решения системы линейных уравнений (4.18) воспользуемся итерационным методом Гаусса-Зейделя. Перепишем (4.18) в матричном виде: (4.14) Матрица А...
-
Эклиптическая система координат - Общие сведения о небесных сферах
Эклиптическая система координат, или эклиптикальные координаты -- это система небесных координат, в которой основной плоскостью является плоскость...
-
Экваториальная система координат Система координат, в которой отсчет производится от плоскости экватора, называется экваториальной. Угловое расстояние...
-
Введение, Движение луны - Характеристика Луны как небесного тела
ЛУНА, единственный естественный спутник Земли и ближайшее к нам небесное тело; среднее расстояние до Луны - 384000 километров. Движение луны Луна...
-
Уравнения движения МКА Рассмотрим невозмущенное движение материальных точек М и m в некоторой инерциальной системе координат. Движение совершается под...
-
В системах двух массивных тел, вращающихся вокруг общего барицентра с постоянной угловой скоростью, существует пять точек, будучи помещенным в которые,...
-
Исследование зависимости энергетики поддержания гало-орбиты от места и направления исполнения импульса Суммарный импульс, затрачиваемый на коррекции для...
-
Закон Всемирного тяготения - Законы движения небесных тел и строение Солнечной системы
Законы Кеплера прекрасно описывали наблюдаемое движение планет, но не вскрывали причин, приводящих к такому движению (напр. вполне можно было считать,...
-
Двумя наиболее значительными успехами классического естествознания, основанного на механике Ньютона, были практически исчерпывающее описание наблюдаемого...
-
Типы ограниченных орбит вокруг точки L2 системы Солнце-Земля Анализируя решение (2.4) линеаризованной системы (2.3), можно заключить, что амплитуды...
-
Математическое описание модели Прямое солнечное излучение на модели КА рассчитывается аналогичным образом как для поверхности Луны, т. е. делая допущения...
-
Под небесными объектами, сближающимися с орбитой Земли, понимают астероиды и кометы, чьи орбиты имеют перигелийные расстояния менее 1.3 астрономической...
-
Это как правило, большие каменные глыбы, которые приходят из пояса астероидов, расположенного между орбитами Марса и Юпитера. Иногда их орбиты изменяются...
-
Покажем, что для любой классической системы, обладающей центральной симметрией и заданной энергией, существует такая метрика, что действие системы будет...
-
Уравнения движения сплошной среды - Теория полета (аэродинамика и динамика полета)
В теоретической механике известно уравнение количества движения материальной точки: , Где в правой части равенства стоит сумма всех действующих на нее...
-
Характеристика орбиты - Исследование движения центра масс малого космического аппарата (МКА)
Для решения задач наблюдения Земли из космоса с хорошим разрешением при жестких ограничениях на массу КА и минимизации затрат на выведение целесообразно...
-
Поскольку решения уравнений (2.2), описывающих движение КА в окрестности точек либрации, являются неустойчивыми, поиск начальных условий, приводящих к...
-
Направление неустойчивости является направлением, исполнение импульса в котором наиболее эффективно. На основе методики, изложенной в разделе 4, был...
-
Целью работы является разработка инструментария, позволяющего рассчитывать траектории перелета от Земли в окрестность точки либрации L2 системы...
-
В этой части мы сведем дифференциальные уравнения (2.1.6) к квадратурам, которые и будут в дальнейшем использованы для построения промежуточной орбиты...
-
В предыдущих главах были выведены формулы, позволяющие вычислять положение спутника в пространстве для любого момента времени, если известны численные...
Моделирование траектории движения небесных тел, Уравнения орбиты в относительных координатах - Математическое моделирование движения небесных тел