Метод Гаусса-Зейделя решения систем линейных уравнений, Алгоритм Z-буфера - Моделирование воздействия теплового излучения на элементы космического аппарата
Для решения системы линейных уравнений (4.18) воспользуемся итерационным методом Гаусса-Зейделя. Перепишем (4.18) в матричном виде:
(4.14)
Матрица А разлагается на нижнюю треугольную с главной диагональю и верхнюю треугольную U:

(4.15)
Тогда система преобразуется:
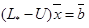
(4.16)
И переписывая как итерационный процесс:
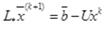
(4.17)
Где и k-ое и (k+1)-ое приближение точного решения :
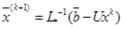
(4.18)
Так как - верхняя треугольная, то компоненты вектора могут быть найдены методом прямой подстановки:
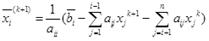
(4.19)
Где i, j = 1, 2, ..., n.
Алгоритм Z-буфера
Преобразования вида
Для определения функции видимости в программе используется алгоритм Z-буфера. Идея метода состоит в том, чтобы поместить камеру в центр излучающего объекта в направлении излучения, затем все объекты рассматриваемой сцены приводятся к системе координат связанной с позицией камеры и направлением ее видимости, из точки позиции камеры моделируется луч в направлении рассматриваемого треугольника, и функция видимости проверяет пересечения луча с остальными объектам сцены. Если зафиксировано несколько пересечений, программа сравнивает расстояние до пересеченных объектов и рассчитывает излучение с ближайшим, отсортировывая остальные [4].
При работе с трехмерными моделями для корректного представления вводятся такие понятия матрицы преобразования камеры и матрицы преобразования вида. Матрица преобразования камеры действуя на вектор координат положения камеры меняет ее положение и ориентацию в заданном фрейме. Матрица вида преобразует все координаты из фрейма сцены в фрейм вида камеры. Определяя матричные операторы как составленные из векторов-столбцов координатных ортов фрейма, получаем для каждого вектора:
(4.20)
Где v - исходный вектор,
М - матричный оператор аффинного преобразования,
V' - преобразованный вектор.
Здесь оператор М - суперпозиция канонических преобразований:
(4.21)
Где Т - оператор трансляции, R - оператор поворота.
Камера является объектом сцены, поэтому для смены положения камеры применяется оператор М. Поскольку сцена рендерится с позиции камеры в пространстве, то для преобразования всех объектов сцены во фрейм камеры, требуется найти преобразование V такое, что:
(4.22)
Где I - единичная матрица. Получаем, что искомое преобразование:
(4.23)
Координатная система камеры образуется тремя ортонормированными векторами, а позиция камеры определяется точкой в исходном фрейме, которая также является началом координат фрейма камеры. По определению камера "смотрит" в направлении, которое можно вычислить, зная точку визирования :
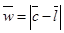
(4.24)
Остальные координатные орты можно определить, используя вектор (0,0,1), тогда:
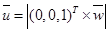
(4.25)
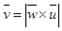
(4.26)
Теперь можно определить оператор преобразования объектов исходной системы координат во фрейм камеры. Объединяя оператор трансляции и оператор поворота в матрицу 4х4, получим оператор изменения положения и ориентации камеры в исходном фрейме:
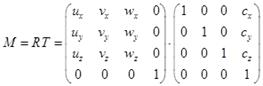
(4.27)
Тогда оператор преобразования сцены во фрейм камеры, определенного вышеописанным образом к единичной матрице, т. е. к исходному фрейму:
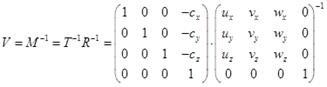
(4.28)
Так как матрица R ортогональная, а, следовательно, симметричная относительно главной диагонали, то R-1= RT, тогда искомый оператор вычисляется как:
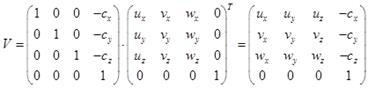
(4.29)
Поиск пересечений луча с объектом
Запишем уравнение луча из начала координат в параметрическом виде:
(4.30)
Где D - нормированный вектор направления луча,
О - начало координат,
T - параметр длины вектора. Положение треугольника определяется координатами его вершин V0, V1, V2.
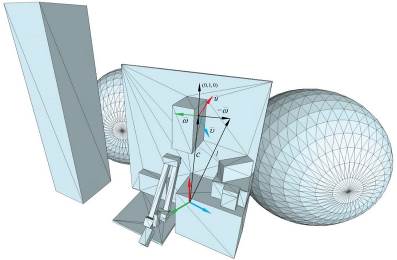
Рис. 4. Расчетная схема преобразований вида
Точка на треугольнике определим как:
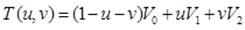
(4.31)
Где (u, v) - барицентрические координаты точки внутри треугольника, если выполняются условия. Пересечение луча и точки на треугольнике равносильно утверждению или:
(4.32)
Уравнение (4.32) может быть записано в матричном виде как:
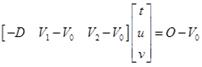
(4.33)
Решая систему линейных уравнений (4.49) находим барицентрические координаты точки пересечения (u, v) и расстояние t до нее от начала координат.
Переобозначим, и. Пользуясь метод Крамера, запишем решение системы линейных уравнений (4.34):
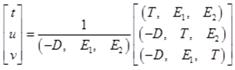
(4.34)
Воспользовавшись свойством перестановки элементов смешанного произведения система (4.50) преобразуется:
(4.35)
Где и.
Похожие статьи
-
Математическое описание модели Прямое солнечное излучение на модели КА рассчитывается аналогичным образом как для поверхности Луны, т. е. делая допущения...
-
Алгоритм вычисления солнечного излучения отраженного от поверхности Луны на конструкции космического аппарата и используемый в расчетной программе...
-
Лунная поверхность места посадки моделируется как плоскость и импортируется в формат STL как дискретизованная поверхность. Модель космического аппарата...
-
Математическое описание модели Модель "Radiocity" Расчет излучения в результате переотражения элементами космического аппарата друг на друга выполнятся с...
-
Физическое описание модели При расчете используется метод моделирования излучения между идеальными диффузными поверхностями или также известными как...
-
Модель принимает на вход: - описание геометрии аппарата в виде твердотельной модели, выполненной в САПР SolidWorks; - описание геометрии поверхности Луны...
-
Программа для расчета коэфициентов, преобразований вида и получений векторов состояния обьектов использует функции описаные в предидущих разделах,...
-
Физическое описание модели При расчете строится аппроксимационная модель поверхности Луны в виде плоскости заданного радиуса. Ориентация плоскости в...
-
Результаты расчета - Моделирование воздействия теплового излучения на элементы космического аппарата
Программа производит расчет излучения на промежутке времени и выводит результаты расчета прямого, отраженного и температурного излучения в заданный...
-
Заключение - Моделирование воздействия теплового излучения на элементы космического аппарата
Был проведен существующих методов тепловых расчетов конструкций, благодаря которому сформировано математическое описание и алгоритм решения поставленной...
-
Аннотация - Моделирование воздействия теплового излучения на элементы космического аппарата
В настоящее время Федеральным Космическим Агентством, совместно с Европейским Космическим Агентством (ESA), разрабатывается проект космической миссии...
-
Постановка задачи - Моделирование воздействия теплового излучения на элементы космического аппарата
В качестве предполагаемого места высадки космического аппарата в составе миссии Луна-Глоб, рассматривается несколько возможных мест посадки космического...
-
Уравнения движения МКА Рассмотрим невозмущенное движение материальных точек М и m в некоторой инерциальной системе координат. Движение совершается под...
-
Стратегиям удержания КА на ограниченных орбитах (гало-орбитах, орбитах Лиссажу и прочих) посвящены многие статьи. В данном разделе приведены краткие...
-
Стратегиям удержания КА на ограниченных орбитах (гало-орбитах, орбитах Лиссажу и прочих) посвящены многие статьи. В данном разделе приведены краткие...
-
Орбиту можно получить как линию пересечения двух поверхностей. Уравнение одной поверхности - это уравнение плоскости орбиты. Уравнение второй поверхности...
-
Направление неустойчивости является направлением, исполнение импульса в котором наиболее эффективно. На основе методики, изложенной в разделе 4, был...
-
Орбиты, для которых были рассчитаны направления неустойчивости в предыдущем разделе, лежат в плоскости эклиптики (плоскости XY). Однако также необходимо...
-
Общее решение уравнений относительного движения - Математическое моделирование движения небесных тел
Рассмотрим на небесной сфере сферический треугольник N M x, где M - проекция текущего положения тела M на небесную сферу. Сторонами этого треугольника...
-
В рамках данной работы производился расчет параметров отлетного вектора при заданных ограничениях на геометрию орбиты. С учетом заданных характеристик Az...
-
Зависимость направления неустойчивости от координат X, Y КА образует поверхность, проекции которой представлены на рис. 36-38. Рис. 36. Точки, для...
-
Расчет направления устойчивости производился для 244 плоских орбит Ляпунова, имеющих следующие начальные координаты: - X = X0 км, -1200000?...
-
Орбитальная система координат - Математическое моделирование движения небесных тел
Орбитальная система координат вводится следующим образом. Ось направим по вектору Лапласа ?, ось - по вектору c, а ось - перпендикулярно к этим осям...
-
Введение - Математическое моделирование движения небесных тел
В небесной механике для описания движений небесных тел в зависимости от конкретных условий используются различные физические модели - идеализированные...
-
Метод оскулирующих элементов - Возмущенное движение космического аппарата
Метод оскулирующих элементов сводится к тому, что исследование возмущенной траектории КА может быть сведено к анализу совокупности невозмущенных...
-
Исследование зависимости энергетики поддержания гало-орбиты от места и направления исполнения импульса Суммарный импульс, затрачиваемый на коррекции для...
-
Направление неустойчивости является направлением, исполнение импульса в котором наиболее эффективно. На основе методики, изложенной в разделе 4, был...
-
Исследование зависимости энергетики поддержания гало-орбиты от места и направления исполнения импульса Суммарный импульс, затрачиваемый на коррекции для...
-
Математическая модель Для описания движения КА по ограниченной орбите введем вращающуюся систему координат, связанную с точкой L2. Центр системы...
-
Точками либрации в ограниченной задаче трех тел, описывающей движение тела малой массы в гравитационном поле, создаваемом двумя массивными телами,...
-
Математическая модель Для описания движения КА по ограниченной орбите введем вращающуюся систему координат, связанную с точкой L2. Центр системы...
-
Зависимость направления неустойчивости от координаты Z - Космический аппарат
Орбиты, для которых были рассчитаны направления неустойчивости в предыдущем разделе, лежат в плоскости эклиптики (плоскости XY). Однако также необходимо...
-
Интерполяция направления неустойчивости - Космический аппарат
Зависимость направления неустойчивости от координат X, Y КА образует поверхность, проекции которой представлены на рис. 36-38. Рис. 36. Точки, для...
-
Результаты расчета направлений устойчивости и неустойчивости - Космический аппарат
Расчет направления устойчивости производился для 244 плоских орбит Ляпунова, имеющих следующие начальные координаты: - X = X0 км, -1200000?...
-
Поскольку характеристики околоземной орбиты зависят от времени старта и космодрома, с которого осуществляется запуск, далеко не все комбинации...
-
В реальности невозможно определить вектор состояния космического аппарата с бесконечной точностью. Кроме того, существуют также технические ограничения...
-
2.1 Дифференциальные уравнения движения искусственного спутника Мы ввели подвижную, жестко связанную с Землей, систему координат и соответствующие ей...
-
Алгоритм подбора начальной скорости и величины корректирующего импульса Описанные алгоритмы были реализованы в программе GMAT (General Mission Analysis...
-
Как было сказано выше, в реальности существуют технические ограничения на точность определения положения КА, скорости КА, а также величину и направление...
-
В работе была разработана методика расчета гало-орбит вокруг точки либрации L2 системы Солнце-Земля. Для расчета начальной скорости КА и величин...
Метод Гаусса-Зейделя решения систем линейных уравнений, Алгоритм Z-буфера - Моделирование воздействия теплового излучения на элементы космического аппарата