Стационарные состояния классических систем - Аномальное движение орбит в общей теории относительности
Покажем, что для любой классической системы, обладающей центральной симметрией и заданной энергией, существует такая метрика, что действие системы будет связано с некоторым решением уравнения (7). Для определенности рассмотрим четырехмерное пространство-время, тогда метрика (4) принимает вид
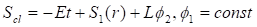
В случае стационарных состояний и траекторий, лежащих в одной "плоскости", действие системы можно представить в виде. Используя уравнения (9) и (11), находим
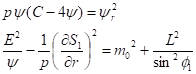
(16)
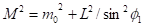
Здесь - масса и угловой момент системы. Далее, положим. Выразим из первого уравнения и подставим во второе, тогда получим
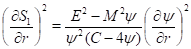
(17)
Решения уравнения (17) при всех вещественных значениях параметров и метрики определены в комплексной плоскости. Действительно, уравнение (17) можно представить в виде
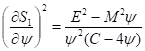
(18)
Отсюда следует, что функция действия в общем случае либо является комплексной, либо движение ограничено условием
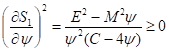
(19)
Поскольку же метрика допускает любые движения, то отсюда следует, что функция действия является комплексной. Разрешая уравнение (18), находим в явном виде зависимость действия стационарных систем от метрики окружающего пространства [9-12]
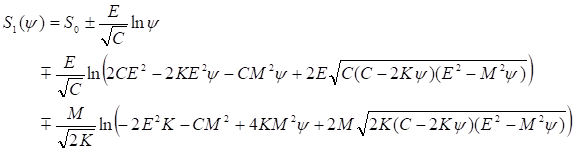
(20)
Здесь логарифмическая функция определена в комплексной плоскости, - произвольная постоянная, в случае четырехмерного пространства-времени.
В случае решение уравнения (18) имеет вид
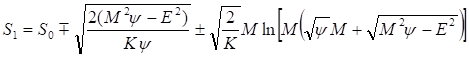
(21)
Полученные зависимости (20)-(21) решают поставленную задачу. Таким образом, мы доказали, что действие любой классической механической системы, находящейся в стационарном состоянии, зависит от параметров, характеризующих движение и от метрики окружающего пространства. Следовательно, для каждого типа движения существует такое уравнение состояния, что движение полностью определяется метрикой и параметрами движения - энергией и угловым моментом, что и требовалось доказать.
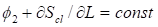
Зависимость от угла определяется в виде. Отсюда находим
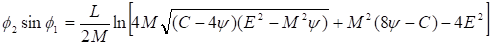
(22)
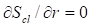
Замкнутые круговые траектории удовлетворяют уравнению. Чтобы траектория была замкнутой, достаточно будет потребовать в уравнении (17) , отсюда находим
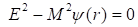
(23)
Смещение перигелия Меркурия в метрике Шварцшильда
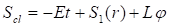
В случае метрики Шварцшильда (12) положим, , тогда уравнение Гамильтона-Якоби принимает вид [4]:
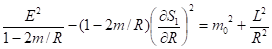
(24)
Разрешая уравнение (24), находим
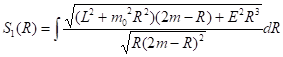
(25)
Дальнейший анализ [4] основан на построении теории возмущений для интеграла (25). Основная идея сводится к тому, что подынтегральное выражение (25) содержит два малых параметра:
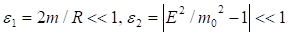
. (26)
Первое из этих неравенств означает, что гравитационный радиус центрального тела значительно меньше, чем радиус орбиты планеты, а второе неравенство характеризует степень малости энергии движения тела по сравнению с энергией покоя. Разложение покоренного выражения под знаком интеграла (25) по двум малым параметрам имеет вид:
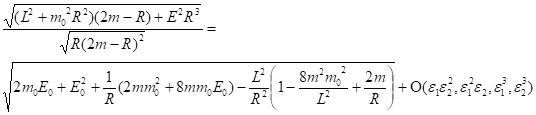
(27)
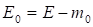
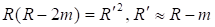
Здесь. Заметим, что при формальном разложении в ряд желаемый ответ [1] сразу не получается. Поэтому авторы [4] использовали еще замену переменной интегрирования: . В этом случае выражение (25) приводится к виду
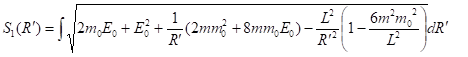
(28)
Такой же ответ можно получить, если вместо замены переменной в выражении (27) использовать оптимальную траекторию для оценки слагаемого. Полагая, что для круговой классической траектории выполняется условие равновесия на орбите, находим
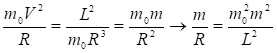
(29)
Подставляя выражение из (29) в (27), приходим к искомому интегралу (28), в котором следует сделать замену. Очевидно, что в этом случае даже если не знать правильного ответа, формальный ряд приводит к правильному выражению (28), но за счет использования гипотезы (29). Запишем действие для невозмущенного движения в виде
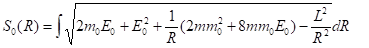
(30)
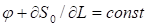
Тогда траектория определяется из уравнения, что дает
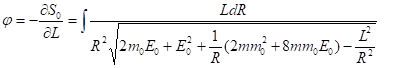
(31)
С другой стороны, для возмущенного движения имеем
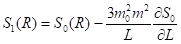
(32)
Сравнивая (31) и (32), находим окончательно, что за один цикл движения угол изменится на величину
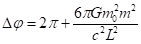
(33)
Здесь мы восстановили размерность всех величин. Обычно изменение угла выражают через большую полуось и эксцентриситет орбиты в виде [1]
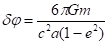
(34)
Экспериментальный результат для Меркурия составляет угловых секунд в столетие, в полном соответствии с выражением (34), которое дает угловых секунд в столетие. Однако решения [1, 4] не являются точными. Отметим, что Фок [5] и Вайнберг [6], используя приближенные решения динамических уравнений, также получили выражение (34) для смещения перигелия. Покажем, что движение тел в метрике [3] приводит к выражению (34).
Смещение перигелия Меркурия в метрике Катанаева [4]
Рассмотрим движение тел в метрике
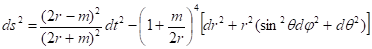
(35)
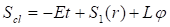
Положим, , тогда уравнение Гамильтона-Якоби можно представить в форме:
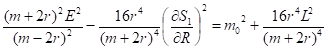
(36)
Уравнение Гамильтона-Якоби (36) можно проинтегрировать и привести к виду
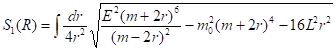
(37)
Разложим покоренное выражение под знаком интеграла (37) по двум малым параметрам (25), в результате получим:
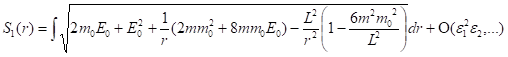
(38)
И так, мы получили выражение типа (28), из которого автоматически следует формула Эйнштейна (34) без каких-либо дополнительных гипотез. Следовательно, в метрике (35) можно было бы получить формулу Эйнштейна (34), не зная конечного ответа. В этой связи заметим, что Эйнштейн при вычислении смещения перигелия Меркурия в работе [1] знал величину аномального смещения - , а также предполагал, что этот эффект нельзя объяснить на основе теории Ньютона.
Однако релятивистская поправка к угловому моменту вращения в уравнении (38) выглядит вполне классической. Кроме того, неизвестно, является ли приближенное решение задачи, полученное выше, а также авторами [1, 4-6] и другими достаточно точным. Иными словами, не является ли полученный результат (34) просто подгонкой под эксперимент или, как предполагает Вайнберг [6], простым совпадением.
Здесь возникает два вопроса: во-первых, о нахождении точного решения задачи хотя бы в одной метрике и, во-вторых, о неклассических эффектах общей теории относительности, которые можно было бы наблюдать в Солнечной системе [13-14].
Оценка влияния космологической постоянной на смещение перигелия Меркурия сделана в работе [14]. Было установлено, что в пределах экспериментальной ошибки эффект не может быть обнаружен. Покажем, что существует еще один эффект, которого нет ни в приближенных теориях типа [1, 4-6], ни в моделях типа [13], но который вполне может быть сопоставим с величиной аномальной прецессии орбиты Меркурия.
Похожие статьи
-
Введение - Аномальное движение орбит в общей теории относительности
Как известно, в общей теории относительности можно определить аномальное движение орбит [1]. Для решения задачи о вековом аномальном смещении перигелия...
-
Аномальные радиальные колебания орбит - Аномальное движение орбит в общей теории относительности
В общем случае уравнения движения материальной точки в гравитационном поле имеют вид [3,6,11-12] (39) Вычисляя коэффициенты аффинной связности в метрике...
-
Уравнения гравитационного поля Эйнштейна имеют вид [4-8]: (1) - тензор Риччи, метрический тензор и тензор энергии-импульса; - космологическая постоянная...
-
Литература - Аномальное движение орбит в общей теории относительности
Albert Einstein. Erklarung der Perihelbeivegung der Merkur aus der allgemeinen Relativitdtstheorie. Sitzungsber. preuss. Akad. Wiss., 1915, 47, 2,...
-
Общее решение уравнений относительного движения - Математическое моделирование движения небесных тел
Рассмотрим на небесной сфере сферический треугольник N M x, где M - проекция текущего положения тела M на небесную сферу. Сторонами этого треугольника...
-
Будем рассматривать эволюцию звезд в рамках модифицированной теории Эйнштейна [23-24]. Уравнения гравитационного поля Эйнштейна имеют вид: (24) - тензор...
-
Общая теория относительности - Классические теории гравитации
В стандартном подходе общей теории относительности (ОТО) гравитация рассматривается изначально не как силовое взаимодействие, а как проявление...
-
Стратегиям удержания КА на ограниченных орбитах (гало-орбитах, орбитах Лиссажу и прочих) посвящены многие статьи. В данном разделе приведены краткие...
-
Полученные дифференциальные уравнения для элементов промежуточной орбиты позволяют довольно просто построить аналитическую теорию движения спутника со...
-
Орбиту можно получить как линию пересечения двух поверхностей. Уравнение одной поверхности - это уравнение плоскости орбиты. Уравнение второй поверхности...
-
Уравнения движения сплошной среды - Теория полета (аэродинамика и динамика полета)
В теоретической механике известно уравнение количества движения материальной точки: , Где в правой части равенства стоит сумма всех действующих на нее...
-
Солнце., Движение солнечной системы - Измерение количественных и качественных характеристик звезд
Солнце ближе к нам, чем другие звезды, поэтому его можно изучить особенно подробно, и сравнивать характеристики других звезд уже с характеристиками...
-
Стратегиям удержания КА на ограниченных орбитах (гало-орбитах, орбитах Лиссажу и прочих) посвящены многие статьи. В данном разделе приведены краткие...
-
2.1 Дифференциальные уравнения движения искусственного спутника Мы ввели подвижную, жестко связанную с Землей, систему координат и соответствующие ей...
-
Здесь рассматривается межорбитальная транспортная система по своему построению аналогичная той, что исследована в работах [1, 2], однако дополнительно...
-
Общее решение задачи двух тел можно получить из общего интеграла, представляющего собой не что иное, как неявную форму задания общего решения. Общее...
-
Влияние электромагнитных сил - Движение искусственного спутника Земли в нецентральном поле тяготения
Пусть спутник обладает электрическим зарядом, равным Q. Тогда при движении в магнитном поле Земли на него будет действовать сила F, определяемая формулой...
-
Введение - Математическое моделирование движения небесных тел
В небесной механике для описания движений небесных тел в зависимости от конкретных условий используются различные физические модели - идеализированные...
-
Математическая модель В данной работе, для описания движения КА, была использована вращающаяся система координат с фиксированным направлением...
-
4.1 Введение В предыдущих главах было подробно изучено промежуточное движение искусственного спутника. Была рассмотрена качественная картина движения,...
-
В предыдущих главах были выведены формулы, позволяющие вычислять положение спутника в пространстве для любого момента времени, если известны численные...
-
Небесная механика и некоторые ее задачи - Классические теории гравитации
Раздел механики, изучающий движение тел в пустом пространстве только под действием гравитации, называется небесной механикой. Наиболее простой задачей...
-
Небулярная теория Лапласа - Обзор основных теорий происхождения Солнечной системы
В 1796 году французский математик и астроном Пьер-Симон Лаплас выдвинул теорию, несколько отличную от предыдущей. Лаплас полагал, что Солнце существовало...
-
В данной работе проводится исследование движения центра масс МКА под действием различных возмущающих ускорений (от нецентральности гравитационного поля...
-
Общие характеристики планет и тел солнечной системы, Меркурий - Строение Солнечной системы
Меркурий Солнечная система планета спутник Меркурий -- четвертая по блеску планета: в максимуме блеска она почти так же ярка, как Сириус, ярче нее бывают...
-
Теория Канта - Основопологающие теории происхождение солнечной системы
Через несколько лет после появления во Франции гипотезы Бюффона, а точнее в 1755-м году, в Германии известный философ Иммануил Кант, будучи еще молодым...
-
Модель нуклонов - Геометрическая турбулентность и эволюция звезд
Влияние векторного потенциала на параметры барионов исследовалось в работе [12]. Было установлено, что масштаб изменения параметров векторного поля...
-
" Наука совершенствуется опытом " Фрэнсис Бэкон (1561 - 1626) Все существующие космические летательные аппараты передвигаются за счет инерции,...
-
Система Птолемея - Движение планет
Становление астрономии как точной науки началось благодаря работам выдающегося греческого ученого Гиппарха. Он первый начал систематические...
-
Метрика пузыря - Геометрическая турбулентность и эволюция звезд
В метрике (2) можно определить дефект решетки типа пузыря. В области пузыря считаем, что, а во внешней области решение зададим в виде (2), имеем (4) На...
-
Постановка задачи Долготная часть потенциала земного притяжения дается следующей формулой: (6.1.1) Где r -- радиус-вектор; -- геоцентрическая широта; --...
-
Гипотезы о происхождении солнечной системы - Теория происхождения Солнечной системы
К настоящему времени известны многие гипотезы о происхождении Солнечной системы, в том числе предложенные независимо немецким философом И. Кантом...
-
Закон Всемирного тяготения - Законы движения небесных тел и строение Солнечной системы
Законы Кеплера прекрасно описывали наблюдаемое движение планет, но не вскрывали причин, приводящих к такому движению (напр. вполне можно было считать,...
-
Параболическое движение, Прямолинейное движение - Математическое моделирование движения небесных тел
(p = 0, e = 1) Уравнение параболической орбиты записывают в видеp r = 1 + cos v (1.80) Где величина определяет расстояние от центра притяжения M0 до...
-
Гиперболическое движение - Математическое моделирование движения небесных тел
(p=0,e>1) Каноническое уравнение гиперболы в центральных прямоугольных координатах O?!?! представляется в виде (1.68) Где a - действительная, а b...
-
Работы над многоразовым орбитальным кораблем были начаты в 1974 году в рамках подготовки "Комплексной программы НПО "Энергия". Это направление работ было...
-
В рамках данной работы производился расчет параметров отлетного вектора при заданных ограничениях на геометрию орбиты. С учетом заданных характеристик Az...
-
Блок-схема, представленная на Рис.2. 2 в предыдущем разделе, подходит для описания алгоритма подбора величины импульса. Как было замечено ранее, чтобы...
-
Поскольку решения уравнений (2.2), описывающих движение КА в окрестности точек либрации, являются неустойчивыми, поиск начальных условий, приводящих к...
-
Интегрирование уравнений движения осуществляется численно, поэтому начальные условия, обеспечивающие минимизацию возрастающей компоненты, подбираются...
Стационарные состояния классических систем - Аномальное движение орбит в общей теории относительности