Параболическое движение, Прямолинейное движение - Математическое моделирование движения небесных тел
(p = 0, e = 1)
Уравнение параболической орбиты записывают в видеp r = 1 + cos v
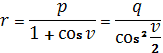
(1.80)
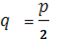
Где величина определяет расстояние от центра притяжения M0 до вершины параболы. Величину q называют перицентрическим расстоянием для параболы. Ее обычно используют в качестве кеплеровского элемента вместо фокального параметра орбиты p.
Для вычисления интеграла
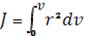
Сделаем замену переменной интегрирования по формуле
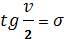
(1.81)
Учитывая, что ? =0 при v = 0, а также
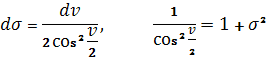
(1.82)
Получим:
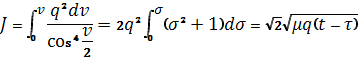
(1.83)
Вычисление определенного интеграла приводит к уравнению Баркера:
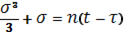
(1.84)
Где введено обозначение
Определение величины ? из этого уравнения по заданному времени t обычно проводят численно, так как известная формула Кардано мало пригодна для вычислений.
Прямолинейное движение
(p = 0, e = 1)
Попытка интегрирования уравнения
Для прямолинейного движения не приводит к получению недостающего первого интеграла, содержащего явно время, а лишь определяет уравнение прямой в полярных координатах:
И v=const. Это уравнение показывает, что прямолинейная траектория всегда проходит через начало координат M0.
Для получения недостающего интеграла используем интеграл энергии. Модуль скорости в случае прямолинейного движения не содержит трансверсальной составляющей, т. е., а интеграл энергии (1.40) для прямолинейного движения запишется в виде
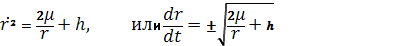
(1.85)
Разделяя переменные, приходим к квадратуре
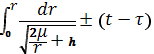
Где ? - время прохождения через перицентр, совпадающее (в прямолинейном движении) с моментом соударения тел.
Левая часть уравнения (1.174) легко вычисляется, но результат зависит от знака постоянной интеграла энергии h.
Возможны следующие три случая:
,
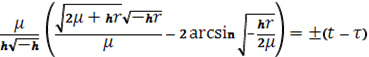
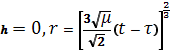
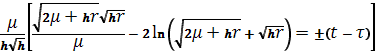
, (1.86)
Для заданного момента времени t в случае h=0 величины r и r? легко вычисляются в конечном виде:
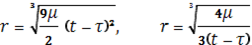
(1.87)
Для случаев h=0 при определении r приходится иметь дело с трансцендентными уравнениями, решать которые можно лишь приближенно с помощью численных методов.
Полагая, e=1, из формул эллиптического движения для определения значений r и r? получим систему уравнений:
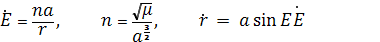
(1.88)
Определяющих прямолинейно-эллиптическое движение.
Аналогично из формул гиперболического движения получим
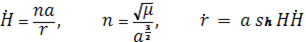
(1.89)
Т. е. уравнения для прямолинейно-гиперболических движений.
Кеплеровскими элементами прямолинейной орбиты кроме уже использованных a, e =1 и ? являются также два угла, характеризующих направление прямой в пространстве.
Ориентация прямолинейной траектории в пространстве определяется вектором ?, исходящим из начала координат M0. Направление вектора ? можно задать двумя углами, например, долготой и широтой. Но чтобы для прямолинейной орбиты сохранить прежние кеплеровские элементы, необходимо из трех элементов ?, ? и i выбрать два, играющих роль долготы и широты, а третий элемент положить равным некоторому значению, сохраняющему зависимости (1.90) и (1.91). Это можно осуществить, полагая, например, i = 90?, а элементы ? и ? тогда будут определять ориентацию прямой в пространстве. Возможны и другие способы выбора угловых элементов. Общее число независимых кеплеровских элементов прямолинейной орбиты равно четырем: a,?,? и ?.
Для случая h=0 прямолинейно-параболическая орбита будет характеризоваться тремя независимыми элементами, так как величина a из элементов исключается (a >? при h >0). Наряду с круговым движением для прямолинейно-параболической орбиты определение координат и скоростей осуществляется по конечным формулам без использования приближенных методов решения нелинейных уравнений.
,
,
,
,
,
, (1.90)
Где наклонение i положено равным 90?.
Орбитальные координаты для прямолинейного движения не определены, так как не определена плоскость орбиты.
Небесный орбита координата бине
Похожие статьи
-
Круговое движение, Эллиптическое движение - Математическое моделирование движения небесных тел
(p = 0, e = 0) Круговое движение представляет собой наиболее простой случай движения в задаче двух тел. Только для кругового движения (и прямолинейного...
-
Гиперболическое движение - Математическое моделирование движения небесных тел
(p=0,e>1) Каноническое уравнение гиперболы в центральных прямоугольных координатах O?!?! представляется в виде (1.68) Где a - действительная, а b...
-
Общее решение задачи двух тел можно получить из общего интеграла, представляющего собой не что иное, как неявную форму задания общего решения. Общее...
-
Общее решение уравнений относительного движения - Математическое моделирование движения небесных тел
Рассмотрим на небесной сфере сферический треугольник N M x, где M - проекция текущего положения тела M на небесную сферу. Сторонами этого треугольника...
-
Уравнение Бине - Математическое моделирование движения небесных тел
Другой способ получения траектории движения в задаче двух тел связан с широко известным уравнением Бине. Это уравнение записывается в цилиндрической...
-
Орбиту можно получить как линию пересечения двух поверхностей. Уравнение одной поверхности - это уравнение плоскости орбиты. Уравнение второй поверхности...
-
Результаты проведенного интегрирования позволяют Сформулировать два первых обобщенных закона Кеплера. Первый закон: невозмущенной орбитой является кривая...
-
Кеплеровские элементы орбиты - Математическое моделирование движения небесных тел
Вместо произвольных постоянных c1,c2,c3,h,?1,?2,?3,? в астрономии обычно используются более наглядные и более удобные постоянные...
-
Лунная поверхность места посадки моделируется как плоскость и импортируется в формат STL как дискретизованная поверхность. Модель космического аппарата...
-
Введение - Математическое моделирование движения небесных тел
В небесной механике для описания движений небесных тел в зависимости от конкретных условий используются различные физические модели - идеализированные...
-
Закон Всемирного тяготения - Законы движения небесных тел и строение Солнечной системы
Законы Кеплера прекрасно описывали наблюдаемое движение планет, но не вскрывали причин, приводящих к такому движению (напр. вполне можно было считать,...
-
Орбитальная система координат - Математическое моделирование движения небесных тел
Орбитальная система координат вводится следующим образом. Ось направим по вектору Лапласа ?, ось - по вектору c, а ось - перпендикулярно к этим осям...
-
Полученные дифференциальные уравнения для элементов промежуточной орбиты позволяют довольно просто построить аналитическую теорию движения спутника со...
-
Заключение - Математическое моделирование движения небесных тел
Небесная механика на протяжении всей истории ее становления была источником новых идей, методов и даже новых направлений в математике, традиционно...
-
Рассмотрим, наконец, общую схему вычисления возмущенных координат спутника. Элементы орбиты. Примем за основную систему произвольных постоянных теории...
-
4.1 Введение В предыдущих главах было подробно изучено промежуточное движение искусственного спутника. Была рассмотрена качественная картина движения,...
-
Притяжение объемного тела - Движение искусственного спутника Земли в нецентральном поле тяготения
Рассмотрим задачу о притяжении материальной точки Р единичной массы некоторым телом М. Будем предполагать, что тело имеет произвольную форму, а плотность...
-
Двумя наиболее значительными успехами классического естествознания, основанного на механике Ньютона, были практически исчерпывающее описание наблюдаемого...
-
Строение Солнечной системы - Законы движения небесных тел и строение Солнечной системы
Хорошо известно, что основная масса Солнечной системы (около 99.8%) приходится на ее единственную звезду - Солнце. Суммарная масса планет составляет...
-
Введение, Движение луны - Характеристика Луны как небесного тела
ЛУНА, единственный естественный спутник Земли и ближайшее к нам небесное тело; среднее расстояние до Луны - 384000 километров. Движение луны Луна...
-
Влияние электромагнитных сил - Движение искусственного спутника Земли в нецентральном поле тяготения
Пусть спутник обладает электрическим зарядом, равным Q. Тогда при движении в магнитном поле Земли на него будет действовать сила F, определяемая формулой...
-
2.1 Дифференциальные уравнения движения искусственного спутника Мы ввели подвижную, жестко связанную с Землей, систему координат и соответствующие ей...
-
Математическое описание модели Модель "Radiocity" Расчет излучения в результате переотражения элементами космического аппарата друг на друга выполнятся с...
-
Сравнивая дуги, на которые перемещаются планеты за равные промежутки времени, установить, какая из планет быстрее движется на звездном небе, и объяснить...
-
Сводка формул для возмущений - Движение искусственного спутника Земли в нецентральном поле тяготения
Приведем окончательные формулы для возмущений элементов промежуточной орбиты. Поскольку v отличается от только периодическими членами порядка и, то с...
-
Представим возмущающую функцию в следующем виде: (6.2.1) Где (6.2.2) (6.2.3) В формулах (6.2.1) и (6.2.2) первые строчки соответствуют четным h -- q, а...
-
Нецентральность гравитационного поля Земли - Возмущенное движение космического аппарата
Возмущенный движение гравитационный орбита При решении ограниченной задачи двух тел Земля представляется шаром со сферическим распределением плотности. В...
-
Аномальные радиальные колебания орбит - Аномальное движение орбит в общей теории относительности
В общем случае уравнения движения материальной точки в гравитационном поле имеют вид [3,6,11-12] (39) Вычисляя коэффициенты аффинной связности в метрике...
-
В предыдущих главах были выведены формулы, позволяющие вычислять положение спутника в пространстве для любого момента времени, если известны численные...
-
Математическое описание модели Прямое солнечное излучение на модели КА рассчитывается аналогичным образом как для поверхности Луны, т. е. делая допущения...
-
Уравнения движения МКА Рассмотрим невозмущенное движение материальных точек М и m в некоторой инерциальной системе координат. Движение совершается под...
-
Исследование зависимости энергетики поддержания гало-орбиты от места и направления исполнения импульса Суммарный импульс, затрачиваемый на коррекции для...
-
Направление неустойчивости является направлением, исполнение импульса в котором наиболее эффективно. На основе методики, изложенной в разделе 4, был...
-
Спектральный анализ небесных тел - Астрономия наших дней
Могучим оружием о исследовании Вселенной стал для астрономов спектральный анализ - изучение интенсивности излучения в отдельных спектральных линиях, в...
-
Мы конкретизировали понятия, используемые в рассматриваемой области, но нужно еще указать характеристики телескопа, предпочтительные с точки зрения...
-
Направление неустойчивости является направлением, исполнение импульса в котором наиболее эффективно. На основе методики, изложенной в разделе 4, был...
-
Покажем, что для любой классической системы, обладающей центральной симметрией и заданной энергией, существует такая метрика, что действие системы будет...
-
Сила сопротивления атмосферы - Движение искусственного спутника Земли в нецентральном поле тяготения
При изучении поступательного движения спутника принимают во внимание лишь ту компоненту аэродинамических сил, направление которой противоположно вектору...
-
Метод оскулирующих элементов - Возмущенное движение космического аппарата
Метод оскулирующих элементов сводится к тому, что исследование возмущенной траектории КА может быть сведено к анализу совокупности невозмущенных...
-
В этой части мы сведем дифференциальные уравнения (2.1.6) к квадратурам, которые и будут в дальнейшем использованы для построения промежуточной орбиты...
Параболическое движение, Прямолинейное движение - Математическое моделирование движения небесных тел