Вариант 2 - Теория игр
Найти все максиминные и минимаксные стратегии игроков, нижнюю и верхнюю цены игры. Указать все ситуации равновесия и решение игры.

Принцип построения стратегии x, основанный на максимизации минимального выигрыша,-- принципом максимина, а выбираемая в соответствии с этим принципом стратегия x -- максиминной стратегией игрока 1.
Принцип построения стратегии у, основанный на минимизации максимальных потерь, называется принципом минимакса, а выбираемая в соответствии с этим принципом стратегия у-- минимаксной стратегией игрока 2.

При заданных условиях


Верхняя цена игры равна нижней цене игры и равна -2.
В антагонистической игре Г = (X, Y, K) ситуация (x? , y?) называется ситуацией равновесия или седловой точкой, если K(x, y?) ? K(x? , y?), K(x?, y) ? K(x ? , y?) для всех x ? X и y ? Y. Т. е. в седловой точке элемент матрицы ai ?j ? является одновременно минимумом в своей строке и максимумом в своем столбце.
В заданной задаче ситуация (x2 , y2) является ситуацией равновесия. Решение игры Г=(2,2,-2). Найти ситуацию равновесия и решение игры в смешанных стратегиях графоаналитическим методом.

Игра решается графически, поскольку игрок имеет только две стратегии. При этом игра рассматривается с позиции игрока.
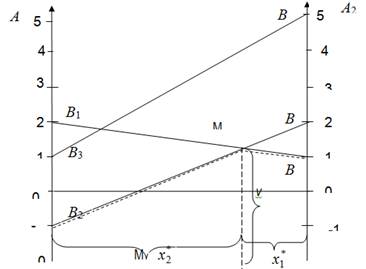
Рис. 1 - Решение матричной игры графическим методом
На координатной плоскости вдоль оси абсцисс отложим отрезок единичной длины. Это ось вероятностей. Перпендикулярно ему проводим оси и, на которых откладываем выигрыши игрока, отвечающие стратегиям и при условиях, что игрок будет применять одну из своих возможных стратегий.






Например, если игрок придерживается своей 1-й стратегии, то выигрыш, который получит игрок, может быть равен -1, если он будет придерживаться своей 1-й стратегии, или может быть равен 2, если игрок В будет придерживаться своей 2-й стратегии. Откладываем эти значения по осям и, соответственно, и соединяем их отрезком прямой, который подписываем. Аналогично строим отрезки прямых, соответствующих остальным двум стратегиям игрока В. Ломаная линия является нижней границей возможного выигрыша игрока. На этой границе находим точку с максимальной ординатой. Видно, что это точка образованная пересечением линий и, которые отвечают стратегиям и игрока. Это означает, что стратегии и являются активными стратегиями игрока, других стратегий он не применяет. Ординатой точки является цена игры, а отрезки и, на которые проекция точки разделяет единичный отрезок оси абсцисс, определяют вероятности и, с которыми игрок будет применять стратегии и, соответственно. Целью графического решения является определение активных стратегий каждого из игроков, далее задача решается аналитически.

В активных стратегиях матрица имеет вид:

.


По этой матрице оптимальную стратегию игрока определяет вектор, а игрока - вектор. Для вычисления компонентов вектора рассмотрим игру с позиции игрока, то есть, составим систему уравнений, в которых неизвестными являются вероятности и, с которыми игрок придерживается своих активных стратегий, а также цена игры. Первые два уравнения этой системы в качестве коэффициентов при неизвестных и содержат элементы платежной матрицы активных стратегий, которые записаны в ее столбцах. Поскольку игрок придерживается либо стратегии, или стратегии, то выбор или одной, или другой из этих стратегий - полная группа событий, соответственно, сумма вероятностей этих событий равна единице. Это и описывает третье уравнение системы. Получаем математическую модель задачи линейного программирования:

Решая полученную систему уравнений, находим оптимальный план относительно вероятностей, с которыми игрок использует свои стратегии, и цену игры, соответствующие этому плану:

Решая методом Крамера получаем

Для вычисления вероятностей и, с которыми игрок придерживается своих активных стратегий, запишем систему уравнений относительно неизвестных компонентов и вектора и цены игры, то есть, рассмотрим матричную игру с позиции игрока. Коэффициентами в первых двух уравнениях системы являются элементы платежной матрицы активных стратегий, стоящие в ее строках. Третье уравнение системы описывает вероятность полной группы событий, поскольку игрок выбирает или стратегию с вероятностью, или стратегию с вероятностью и не выбирает другие стратегии.

Решая эту систему уравнений, находим компоненты оптимального плана двойственной задачи, соответствующие вероятностям активных стратегий игрока, и значение функции цели, которое отвечает этому плану:

Видно, что значение цены игры, которое вычислялось согласно оптимальным стратегиям каждого из игроков, одинаково и совпадает с данными, которые были получены при анализе графического решения.
Привести матричную игру к задаче линейного программирования и решить ее, используя симплекс-метод

ТЕОРИЯ.
Решение игры может быть сведено к решению задачи линейного программирования.


Пусть игра задана платежной матрицей . Первый игрок обладает , второй ? стратегиями. Необходимо определить оптимальные стратегии первого и второго игрока, где ? оптимальные частоты применения своих стратегий соответственно первым и вторым игроком.



.
Оптимальная стратегия X* обеспечивает первому игроку средний выигрыш, не меньший, чем цена игры V, при любой стратегии второго игрока и выигрыш, равный цене игры V, при оптимальной стратегии второго игрока.
Если первый игрок применяет смешанную стратегию X* против любой чистой стратегии второго игрока, то он получает средний выигрыш, или математическое ожидание выигрыша V(j)=a1jx1+...amjxm, j= 1, 2,..., п (т. е. элементы j-гo столбца платежной матрицы почленно умножаются на соответствующие вероятности стратегий первого игрока и результаты складываются).
Для оптимальной стратегии X* все средние выигрыши не меньше цены игры V, поэтому получаем систему неравенств:
A11x1+a21x2+...+am1xmV,
A12x1+a22x2+...+am2xmV,
.......................... (1)
A1n x1+a2n x2+...+amn xmV.
Каждое из неравенств можно разделить на число V > 0. Введем новые переменные
Zi=. (2)
Тогда система (1) примет вид:

(3)
Цель первого игрока -- максимизировать свой гарантированный выигрыш, т. е. цену игры V. Разделив на равенство , получаем, что переменные удовлетворяют условию: .
Максимизация цены игры V эквивалентна минимизации величины , поэтому задача может быть сформулирована следующим образом: определить значения переменных так, чтобы они удовлетворяли линейным ограничениям (1.4.3) и при этом линейная функция
(4)
Обращалась в минимум. Это задача линейного программирования. Решая задачу (3) ? (4), получаем оптимальные стратегии .

Для определения оптимальной стратегии второго игрока следует учесть, что он стремится минимизировать гарантированный выигрыш первого игрока, т. е. найти . Переменные удовлетворяют неравенствам

(5)
Которые следуют из того, что средний проигрыш второго игрока не превосходит цены игры, какую бы чистую стратегию не применял первый игрок.
Если обозначить

(6)
То получим систему неравенств:

(7)

Переменные , удовлетворяют условию .

Игра свелась к следующей задаче: определить значения переменных , которые удовлетворяют системе неравенств (1.4.7) и максимизируют линейную функцию
(8)
Решение задачи линейного программирования (7) ? (8) определяет оптимальную стратегию . При этом цена игры

. (9)
Задачи линейного программирования (3) ? (4) и (7) ? (8) являются взаимно двойственными. Очевидно, при определении оптимальных стратегий в конкретных задачах следует выбрать ту из взаимно двойственных задач, решение которой менее трудоемко, а решение другой задачи найти с помощью теорем двойственности.
Решение.

Любая игра сводится к задаче линейного программирования. Для первого игрока ограничения и целевая функция выглядят следующим образом:
Где




Для второго игрока задача линейного программирования является двойственной к предыдущей и имеет вид:

Где


Решим симплекс-методом систему, составленную для второго игрока.
Добавим новые переменные и приведем систему к каноническому виду:

Базис составляют переменные 5 6 7
Находим начальное опорное решение. Для этого свободные переменные приравниваем к нулю 1= 2=3=4= 0.
Получили опорное решение N1 = (0,0,0,0,1,1,1) с единичным базисом Б1 =(А5,А6,А7).
F(N1)=0
Вычисляем оценки разложений векторов условий по базису опорного решения по формуле:
Стратегия игрок игра программирование
Дk = CбNk -- ck
Где:
Cб = (с1, с2, ... , сm) -- вектор коэффициентов целевой функции при базисных переменных
Nk = (1k, 2k, ... , mk) -- вектор разложения соответствующего вектора Ак по базису опорного решения
Ск -- коэффициент целевой функции при переменной к.
Опорное решение, коэффициенты разложений и оценки разложений векторов условий по базису опорного решения запишем в симплексной таблице:
|
1 |
1 |
1 |
1 |
0 |
0 |
0 | ||||
|
Б |
Сб |
А0 |
А1 |
А2 |
А3 |
А4 |
А5 |
А6 |
А7 | |
|
5 |
0 |
1 |
3 |
4 |
6 |
4 |
1 |
0 |
0 |
1/3 |
|
6 |
0 |
1 |
4 |
4 |
4 |
5 |
0 |
1 |
0 |
1/4 |
|
7 |
0 |
1 |
2 |
3 |
6 |
8 |
0 |
0 |
1 |
1/2 |
|
Дk |
0 |
-1 |
-1 |
-1 |
-1 |
0 |
0 |
0 |
Сверху над таблицей для удобства вычислений оценок записываются коэффициенты целевой функции. В первом столбце "Б" записываются векторы, входящие в базис опорного решения. Во втором столбце таблицы "Сб" записываются коэффициенты целевой функции при базисных переменных в том же порядке.
В последней строке таблицы с оценками Дk в столбце "А0" записываются значения целевой функции на опорном решении Z (N1).
По теореме об улучшении опорного решения, если в задаче на максимум хотя бы один вектор имеет отрицательную оценку, то можно найти новое опорное решение, на котором значение целевой функции будет больше.
Так как имеется три одинаковых отрицательных оценки, выберем вектор А1. Наименьшее значение - во второй строке. Значит вводим в базис Х2 переменную 1 вместо 6.
Выполняем преобразования Жордана с элементом х21= 4, получаем второе опорное решение N2 = (0.25; 0; 0; 0;0,25;0;0,5) з базисом Б2 = (А5, А1, А7) (таблица 2)
Стратегия игрок программирование
|
1 |
1 |
1 |
1 |
0 |
0 |
0 | |||
|
Б |
Сб |
А0 |
А1 |
А2 |
А3 |
А4 |
А5 |
А6 |
А7 |
|
5 |
0 |
1/4 |
0 |
1 |
3 |
1/4 |
1 |
- 3/4 |
0 |
|
1 |
1 |
1/4 |
1 |
1 |
1 |
1 1/4 |
0 |
1/4 |
0 |
|
7 |
0 |
1/2 |
0 |
1 |
4 |
5 1/2 |
0 |
- 1/2 |
1 |
|
Дk |
1/4 |
0 |
0 |
0 |
1/4 |
0 |
1/4 |
0 |
Все оценки положительные, то есть решение оптимальное.
Полученное оптимальное решение имеет вид:

Перейдем к исходным переменным:

Из полученных результатов следует, что минимальный гарантированный проигрыш второго игрока составит 4 в случае если он будет использовать только свою первую стратегию.
Решение задачи для первого игрока найдем с помощью теорем двойственности.
Первая теорема двойственности
Для взаимодвойственных ЗЛП имеет место один из взаимоисключающих случаев.

Похожие статьи
-
При решении экономических задач часто анализировать ситуации, в которых сталкиваются интересы двух или более конкурирующих сторон, преследующих различные...
-
Модели теории игр. Основные определения и термины В разных областях целенаправленной деятельности, например при разработке и эксплуатации АСУ, часто...
-
Рассмотрим конечные матричные игры, в которых нет седловой точки, т. е. . Нетрудно доказать, что. Если игра одноходовая, то по принципу минимакса игроку...
-
Теория игр - Математическое моделирование экономических процессов
Одна из задач теории оптимальных решений - принятие решения в условиях неопределенности. Для обоснования решений разработаны специальные математические...
-
Теория игр исследует оптимальные стратегии в ситуациях игрового характера. К ним относятся ситуации, связанные с выбором наивыгоднейших производственных...
-
Пусть у игроков А и В соответственно M и N чистых стратегий, которые обозначим через и. Выбор игроками любой пары стратегий и однозначно определяет исход...
-
В условиях рыночной экономики возникают ситуации, в которых сталкиваются интересы двух и более сторон. Такие ситуации относятся к конфликтным. Например,...
-
Объем выпуска продукции Y зависит от количества вложенного труда x как функция . Цена продукции v, зарплата p. Другие издержки не учитываются. Найти...
-
Теория оптимального программирования - Оптимальное программирование
Оптимальное программирование [optimal programming] -- применение в экономике методов математического программирования. Часто эти термины определяют как...
-
Комментарии к третьему разделу курсовой работы В третьем разделе курсовой работы студенту предлагается определить оптимальную стратегию заказа в условиях...
-
В современной экономической теории доминирующую роль играют труды зарубежных экономистов. Однако русская экономическая наука также ярко представлена...
-
Модель в общем смысле (обобщенная модель) есть создаваемый с целью получения и (или) хранения информации специфический объект (в форме мысленного образа,...
-
Модели линейного программирования. Основные определения Еще одним классом задач экономико-математического моделирования являются задачи линейного...
-
Моделирование в условиях противодействия, игровые модели - Основы теории систем и системного анализа
Как уже неоднократно отмечалось, системный анализ невозможен без учета взаимодействий данной системы с внешней средой. Ранее упоминалась необходимость...
-
Основные понятия и обозначения Динамическое программирование как самостоятельная дисциплина сформировалась в пятидесятых годах двадцатого века. Большой...
-
Игра для двух игроков - Шулеры, или Математическое исследование одной карточной игры
Пусть на круге ( N, k ) играют два игрока. Они делают ходы по очереди. Проигрывает тот, кто не может сделать ход. Кто выигрывает при правильной игре?...
-
Часто используют такой показатель качества алгоритма диагностики, как "вероятность (или доля) правильной классификации (диагностики)" [12, 13] - чем этот...
-
Методы классификации - неотъемлемая часть математических методов исследования, интересная теоретически и важная практически. Обзоры этой научной области...
-
Основные понятия теории экономико-математического моделирования Кибернетический подход к исследованию экономико-математических систем Обычно...
-
Контрольная работа По дисциплине: Теория вероятностей Контрольная работа № 1 Вариант 1 Задача № 1 Условие: Из 10 изделий, среди которых 4 бракованные,...
-
Взаимосвязи случайных событий - Основы теории систем и системного анализа
Вернемся теперь к вопросу о случайных событиях. Здесь методически удобнее рассматривать вначале простые события (может произойти или не произойти)....
-
Прогностическая сила - Базовые результаты математической теории классификации
С целью поиска приемлемого показателя качества диагностики рассмотрим восходящую к Р. Фишеру [20] широко известную параметрическую вероятностную модель...
-
Описание варианта задания - Вероятность безотказной работы
В данной работе необходимо рассчитать вероятность безотказной работы и произвести анализ и оптимизацию полученной по варианту схемы. Для этого...
-
Опытом называется всякое осуществление определенных условий и действий, при которых наблюдается изучаемое случайное явление. Опыты можно характеризовать...
-
Ценностная окраска ситуационных образов, возникающих в сознании членов человеческого сообщества, является основным движущим стимулом, формирующим их...
-
Теория вероятностей и математическая статистика
Задача 1 Малое предприятие имеет два цеха - А и В. Каждому установлен месячный план выпуска продукции. Известно, что цех А свой план выполняет с...
-
Основная теория сезонности временного ряда - Методы изучения сезонных колебаний. Примеры расчетов
Основными составляющими временного ряда являются тренд и сезонная компонента. Составляющие этих рядов могут представлять собой либо тренд, либо сезонную...
-
ТЕМПЕРАТУРА - Основные положения молекулярно-кинетической теории, ее опытные обоснования
Любое макроскопическое тело или группа макроскопических тел называется термодинамической системой. Тепловое или термодинамическое равновесие - такое...
-
Теория затрат - Линейное программирование в экономике
Затраты - это сумма средств (материальных, трудовых, финансовых), использованных в процессе производства. Часто понятие затрат заменяют понятием...
-
Основные понятия линейного программирования - Оптимальное программирование
Математические исследования отдельных экономических проблем, математическая формализация числового материала проводилась еще в XIX веке. При...
-
Методы непараметрической статистики - Основы теории систем и системного анализа
Использование классических распределений случайных величин обычно называют "параметрической статистикой" - мы делаем предположение о том, что...
-
Теория массового обслуживания - Математическое моделирование экономических процессов
Часто приходится сталкиваться с такими ситуациями: - очередь покупателей в кассах магазинов; - колонна автомобилей, движение которых остановлено...
-
Создание теории химического строения - Русский ученый А. М. Бутлеров
Первое публичное выступление А. М. Бутлерова по теоретическим вопросам органической химии относится к концу 50-х годов: его доклад на заседании...
-
СМО с очередью - Теория массового обслуживания
В качестве показателей эффективности СМО с ожиданием, кроме уже известных показателей -- абсолютной A и относительной Q пропускной способности,...
-
Теоретическое описание методов решения задания, СМО с отказами - Теория массового обслуживания
СМО с отказами Одноканальная система (СМО) с отказами Имеется один канал, на который поступает поток заявок с интенсивностью л, поток обслуживания имеет...
-
Пусть { , , ..., } - множество возможных состояний некоторой физической системы. В любой момент времени система может находиться только в одном...
-
Введение - Основные понятия теории вероятностей
Каждая наука, развивающая общую теорию какого-либо круга явлений, содержит ряд основных понятий, на которых она базируется. Таковы, например, в геометрии...
-
"Квантовая химия" Квантовая химия - область теоретической химии, в которой вопросы строения и реакционной способности химических соединений, химические...
-
Следствия теоремы, Послесловие к доказательству - Об одной теореме теории чисел
Не существует ЦЕЛЫХ чисел, для которых выполняется равенство (1). При четных значениях показателя степени уравнение вида (1) идентично как для...
-
Теория массового обслуживания - теория, которая изучает статистические закономерности в массовых операциях, состоящих из большого числа однородных...
Вариант 2 - Теория игр