Теоремы двойственности и их использование в задачах ЛП - Решение оптимизационных экономических задач методами линейного программирования
Исходная задача:
При ограничениях:
Двойственной является следующая задача:
При ограничениях:
Число неизвестных в двойственной задаче равно 2. Следовательно, решение двойственной задачи можно найти графическим методом.
Построим систему координат и проведем прямые, ограничивающие область допустимых решений (ОДР). Для этого в неравенствах системы ограничений и условиях неотрицательности переменных () знаки неравенств заменим на знаки равенств, и для каждой прямой зададим координаты двух точек:
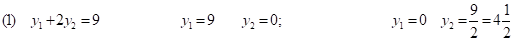
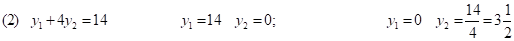

Построим вектор целевой функции W.
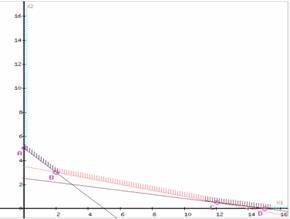
Областью допустимых решений является неограниченная выпуклая многоугольная область.
Далее, среди всех точек области допустимых решений (ОДР) надо найти такую точку, в которой целевая функция W имеет минимальное значение.
Уравнение при фиксированном значении W определяет прямую, а при изменении значения W - семейство параллельных прямых, которые называются Линиями уровня для функции W.
Будем перемещать линию уровня (например, ) по ОДР параллельно самой себе в направлении вектора до тех пор, пока она не пройдет через первую общую точку с ОДР. Координаты этой точки и являются оптимальным решением данной задачи.
Для нахождения координат необходимо решить систему линейных уравнений соответствующих прямым, пересекающимся в данной точке. У нас 4 точки: А, В, С, Д.
Найдем координаты Точки А. Для этого решим систему, составленную из уравнений (4) и (5):
А (0; 5)
Подставим координаты точки А в целевую функцию:
Найдем координаты Точки В. Для этого надо решить систему, составленную из уравнений (3) и (4):
В (3; 2)
Подставим найденные значения в целевую функцию:
Найдем координаты Точки С. Для этого решим систему, составленную из уравнений (3) и (2):
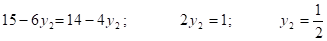
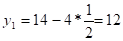
С (12; 1/2)
Подставим найденные координаты точки С в целевую функцию:
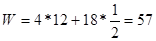
Найдем координаты Точки Д. Для этого решим систему, составленную из уравнений (3) и (6):
Д (15; 0)
Подставим найденные координаты точки Е в целевую функцию:
Среди всех найденных значений целевых функций выбираем наименьшую.
Функция W принимает минимальное значение в точке Д; .
Решим данную задачу, используя теорему двойственности
Т. к. y1>0, то х1+х2+х3+3х4=4
Т. к. y2>0, то 2х1+4х2+6х3+х4=18
F(x)=G(y)= 57 - первая теорема двойственности выполнена, приведенный в условии план является оптимальным.
Проанализируем использование ресурсов:
Подставим y1 и y2 в систему ограничений двойственной задачи.
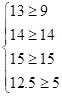
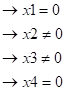
Оставим систему с x3 и x2:
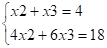
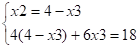
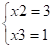
F(x) = 9*0 + 14*3 + 15*1 + 5*0=57
Теорема двойственности.
Если одна из пары двойственных задач имеет оптимальный план, то и другая имеет оптимальный план, причем экстремальные значения целевых функций равны: .
В нашем случае: при решении исходной задачи симплекс-методом была получена функция , а т. к. по теореме двойственности, то, что мы и получили, решая двойственную задачу графическим методом.
Похожие статьи
-
В разделе 1 курсовой работы требуется: Определить количество закупаемого заданным филиалом фирмы сырья у каждого АО, (xj), максимизируя прибыль филиала....
-
Необходимо найти минимальное значение целевой функции F = 4x1+18x2 > min, при системе ограничений: X1+4x2?14(1) X1+6x2?15(2) X1+x2?5(3)...
-
Это раздел математического программирования, изучающий методы решения таких экстремальных задач, в которых результаты (эффективность) возрастают или...
-
Известно оптимальное решение X*=(0;0;1;1) задачи линейного программирования: Составьте двойственную задачу и найдите ее оптимальное решение по теореме...
-
Решим прямую задачу линейного программирования симплексным методом, с использованием симплексной таблицы. Определим максимальное значение целевой...
-
Решение задачи графическим методом - Математическое моделирование в менеджменте и маркетинге
Необходимо найти максимальное значение целевой функции L(x)= 2x1+2x2 > max, при системе ограничений: 6x1+8x2?48, (1) 8x1+11x2?88, (2)...
-
Так как целевая функция не является линейной, то эта задача является задачей нелинейного программирования. Найдем ее решение, используя геометрическую...
-
Математическая модель задачи нелинейного программирования (ЗНП) (*) Для ЗНП в отличие от Задачи Линейного Программирования (ЗЛП) нет единого метода...
-
Как известно решение задач симплексным методом применяется очень часто. Это связано с тем, что симплексный метод подходит для решения широкого круга...
-
Параметрическое линейное программирование - Методы линейного программирования
Представляет собой один из разделов математического программирования, изучающий задачи, в которых целевая функция или ограничения зависят от одного или...
-
Линейное программирование, Общая задача линейного программирования - Экономико-математические методы
Термин "линейное программирование" впервые появился в 1951 г. в работах американских ученых (Дж. Данциг, Т. Купманс), а первые исследования по линейному...
-
Экономико-математические методы и моделирование в землеустройстве позволяют решать большой круг задач, связанных с оптимизацией территориальной...
-
Некоторые особенности решения задач нелинейного программирования - Экономико-математические методы
Для решения ЗНП существенно знать: 1) выпукло или не выпукло множество допустимых решений задачи; 2) является ли целевая функция выпуклой или вогнутой...
-
Динамическое программирование Динамическое программирование -- один из разделов оптимального программирования, в котором процесс принятия решения и...
-
Второй раздел курсовой работы посвящен особенностям постановки и решения общей задачи линейного программирования, а именно, транспортной задаче (ТЗЛП)....
-
Ограничение чувствительность задача программирование Вариации правых частей ограничений приводят к изменению области допустимых решений ЗЛП, в действии...
-
Несмотря на требование линейности функций критериев и ограничений, в рамки линейного программирования попадают многочисленные задачи распределения...
-
Вариации коэффициентов целевой функции ЗЛП приводят к изменению направления вектора градиента. Так как при этом не затрагивается допустимое множество, то...
-
Теория: Применяется, как правило, для задач линейного программирования, содержащих не более 2 переменных. Суть геометрического метода сводится к...
-
В начале пятилетнего периода работы предприятию выделена сумма в C руб. для приобретения нового оборудования. Стоимость одного комплекта оборудования...
-
Исследуем на экстремум функцию: 1. С помощью необходимого существования экстремума, т. е. из системы Найдем координаты стационарных (критических) точек:...
-
Введение - Решение оптимизационных экономических задач методами линейного программирования
Линейное программирование является составной частью раздела математики, который изучает методы нахождения условного экстремума функции многих переменных...
-
Необходимость введения нового ограничения может возникнуть, например, когда первоначально для сокращения затрат машинного времени некоторые интуитивно...
-
Задача о загрузке рюкзака (задача о ранце) - Метод динамического программирования для решения задач
Постановка задачи. Пусть имеются N видов грузов с номерами. Единица груза j-го вида имеет все aJ. Если груз j-го вида берется в количестве xJ, то его...
-
Задачей линейного программирования (ЛП) называется задача минимизации или максимизации линейного функционала при линейных ограничениях. В литературе...
-
Модели линейного программирования. Основные определения Еще одним классом задач экономико-математического моделирования являются задачи линейного...
-
При решении экономических задач часто анализировать ситуации, в которых сталкиваются интересы двух или более конкурирующих сторон, преследующих различные...
-
Основные понятия линейного программирования - Оптимальное программирование
Математические исследования отдельных экономических проблем, математическая формализация числового материала проводилась еще в XIX веке. При...
-
Математическая модель транспортной задачи: F = ??cIjXIj, (1) При условиях: ?xIj = aI, i = 1,2,..., m, (2) ?xIj = bJ, j = 1,2,..., n, (3)...
-
Вид сырья Запас сырья Количество единиц сырья, идущих на изготовление единицы продукции P1 P2 P3 P4 S1 4 1 1 1 3 S2 18 2 4 6 1 Прибыль от единицы...
-
Для достижения поставленной цели предприятию требуются материалы, оборудование, энергия, рабочая сила и другие ресурсы. Каждое предприятие такими...
-
Решение смешанной задачи для уравнения теплопроводности методом конечных разностей
Решение смешанной задачи для уравнения теплопроводности методом конечных разностей 1. Цель работы Ознакомление с методами решения смешанных задач для...
-
Планиметрические задачи Задача 1.Написать уравнения касательной и нормали к графику функциив данной точке, если: [3]. Решение. Уравнение касательной...
-
Элементы матричного анализа - Методы решения системы линейных уравнений
Вектором, как на плоскости, так и в пространстве, называется направленный Отрезок , то есть такой Отрезок , один из концов которого выделен и называется...
-
Системы линейных уравнений - Методы решения системы линейных уравнений
Системой m линейных уравнений с n неизвестными называется система вида Где aIj и bI (i=1,...,m; b=1,...,n) - некоторые известные числа, а x1,...,xN -...
-
Во многих экономических моделях исследования операций зависимости между постоянными и переменными факторами лишь в первом приближении можно считать...
-
Геометрическая интерпретация и графическое решение ЗЛП - Экономико-математические методы
Геометрическая интерпретация экономических задач дает возможность наглядно представить их структуру, выявить особенности и открывает пути исследования...
-
Изучение теоретических вопросов анализа чувствительности оптимального решения ЗЛП к вариациям некоторых параметров задачи и введению нового ограничения....
-
Пусть имеется оптимизационная задача вида: (1) (2) (3) - задан(4) Здесь предполагается, что FJ(xJ,yJ)>0 для всех допустимых значений xJ,yJ. В этом случае...
-
Метод дихотомии требует менее всего итераций цикла для получения корней уравнения с заданной точностью. Если расчет ведется без помощи ЭВМ, то это...
Теоремы двойственности и их использование в задачах ЛП - Решение оптимизационных экономических задач методами линейного программирования