Постановка задачи многокритериальной оптимизации - Многокритериальная оптимизация на основе нейросетевой, нечеткой и нейро-нечеткой аппроксимации функции предпочтений лица, принимающего решения

Пусть - вектор параметров задачи (вектор варьируемых параметров), где - n-мерное арифметическое пространство (пространство параметров). Множеством допустимых значений вектора параметров X является ограниченное замкнутое множество, где П - "технологический" параллелепипед допустимых значений вектора параметров,

,

Множество формируют ограничивающие функции, :

.

Векторный критерий оптимальности

со значениями в пространстве определен в параллелепипеде П. ЛПР стремится минимизировать на множестве каждый из частных критериев оптимальности, что условно записывается в виде

, , (1.1)

Где - искомое решение МКО-задачи.

Введем следующие обозначения: - критериальное множество (множество достижимости) задачи, т. е. множество, в которое векторный критерий оптимальности отображает множество ; - фронт Парето задачи, ; - множество Парето. Если, то будем говорить, что вектор X - эффективный по Парето вектор [Лотов, 1984]. Положим, что частные критерии оптимальности тем или иным образом нормализованы [Карпенко и др., 2008a].

Рассмотрим решение задачи (1.1) методом скалярной свертки. Способ свертки не фиксируется. Обозначим операцию свертки, где - вектор весовых множителей,

-

Множество допустимых значений этого вектора.

При каждом фиксированном векторе метод скалярной свертки сводит решение задачи (1.1) к решению однокритериальной задачи глобальной условной оптимизации

, . (1.2)

В силу ограниченности и замкнутости множества решение этой задачи существует.

Если при каждом решение задачи (1.2) единственно, то это решение ставит в соответствие каждому из допустимых векторов единственный вектор и соответствующие значения частных критериев оптимальности. Данное обстоятельство позволяет полагать, что в этом случае функция предпочтений ЛПР определена не на множестве, а на множестве :

.

В результате МКО-задача сводится к задаче выбора вектора такого, что

, . (1.3)

Поскольку обычно, переход от задачи (1.1) к задаче (1.3) важен с точки зрения уменьшения вычислительных затрат.

Величину будем считать лингвистической переменной со значениями, меняющимися от "Очень-очень плохо" до "Отлично" [Карпенко и др., 2010b]. Обозначим - ядро нечеткой переменной, принимающее значения от 1 до 9.

В результате МКО-задача сводится к задаче отыскания вектора, обеспечивающего максимальное значение дискретной функции :

, .

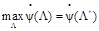
Таким образом, задача сводится к аппроксимации функции предпочтения лица, принимающего решение.

Похожие статьи

• Введение - Многокритериальная оптимизация на основе нейросетевой, нечеткой и нейро-нечеткой аппроксимации функции предпочтений лица, принимающего решения

  Современные инженерные задачи оптимизации многокритериальные. Выделяют класс задач многоцелевой или многокритериальной оптимизации (класс МКО-задач). В...

• Особенности аппроксимации функции предпочтений ЛПР с помощью аппарата нейро-нечеткого вывода, Исследование эффективности методов - Многокритериальная оптимизация на основе нейросетевой, нечеткой и нейро-нечеткой аппроксимации функции предпочтений лица, принимающего решения

  Используется адаптивная нейро-нечеткая система вывода ANFIS, функционально эквивалентная системе нечеткого вывода Сугено. Вывод осуществляется за два...

• Особенности нейросетевой аппроксимации функции предпочтения ЛПР, Особенности аппроксимации функции предпочтений ЛПР с помощью аппарата нечеткой логики - Многокритериальная оптимизация на основе нейросетевой, нечеткой и нейро-нечеткой аппроксимации функции предпочтений лица, принимающего решения

  Аппроксимация функции предпочтения ЛПР нейронными сетями имеет в работе ту особенность, что процесс обучения нейронных сетей происходит в условиях малой...

• Метод решения задачи - Многокритериальная оптимизация на основе нейросетевой, нечеткой и нейро-нечеткой аппроксимации функции предпочтений лица, принимающего решения

  Многокритериальный оптимизация нейронный аппроксимация Общая схема рассматриваемого метода является итерационной и состоит из следующих основных этапов....

• Выводы, Список литературы - Многокритериальная оптимизация на основе нейросетевой, нечеткой и нейро-нечеткой аппроксимации функции предпочтений лица, принимающего решения

  Разработан адаптивный метод решения МКО-задачи, основанный на аппроксимации функции предпочтений ЛПР с помощью нейронных сетей, аппарата нечеткой логики,...

• Свертка скалярных критериев и условия компромисса - Моделирование распределительных процессов на основе динамических задач векторной оптимизации

  Пусть ограничения (4) не противоречивы, т. е. не пусто множество допустимых решений, а оптимальное решение достигается я в точке для каждой K -ой...

• Метод динамического программирования для ЗНП с мультипликативной целевой функцией - Метод динамического программирования для решения задач

  Пусть имеется оптимизационная задача вида: (1) (2) (3) - задан(4) Здесь предполагается, что FJ(xJ,yJ)>0 для всех допустимых значений xJ,yJ. В этом случае...

• Количественный анализ и параметрическая оптимизация - Моделирование распределительных процессов на основе динамических задач векторной оптимизации

  Для примера рассмотрим вытекающую из общей постановки (3),(4) двухкритериальную () многоэтапную динамическую задачу, с целевыми функциями дохода и потерь...

• Введение - Моделирование распределительных процессов на основе динамических задач векторной оптимизации

  Развитие методов многокритериальной оптимизации сложных систем обусловлено необходимостью повышения эффективности их функционирования на основе обобщения...

• Постановка задачи и генетические алгоритмы для многокритериальной оптимизации ИП - Возможности генетических алгоритмов для решения задачи многокритериальной оптимизации инвестиционного портфеля

  Рассматриваемая задача оптимизации ИП основывается на двухкритериальной модели Г. Марковица с незначительной корректировкой (вместо поиска долей каждого...

• Результаты применения МГА для оптимизации ИП - Возможности генетических алгоритмов для решения задачи многокритериальной оптимизации инвестиционного портфеля

  Все генетические алгоритмы участвовали в двух группах тестов. В каждой группе исследовались различные наборы значений управляющих параметров МГА:...

• Геометрическая интерпретация и графическое решение ЗЛП - Экономико-математические методы

  Геометрическая интерпретация экономических задач дает возможность наглядно представить их структуру, выявить особенности и открывает пути исследования...

• Введение - Возможности генетических алгоритмов для решения задачи многокритериальной оптимизации инвестиционного портфеля

  Оптимизация инвестиционного портфеля (ИП) [Дубровин и др., 2008], [Мищенко и др., 2002], [Серов, 2000] является одной из важных экономических задач,...

• Анализ чувствительности оптимального решения ЗЛП к вариациям коэффициентов целевой функции., Графический способ анализа чувствительности оптимального решения к вариациям C[j - Исследование чувствительности оптимального решения задачи линейного программирования к вариациям ее параметров и введению нового ограничения

  Вариации коэффициентов целевой функции ЗЛП приводят к изменению направления вектора градиента. Так как при этом не затрагивается допустимое множество, то...

• Геометрическая интерпретация - Математические методы и модели в экономике

  Геометрическая интерпретация задачи линейного программирования является основой графического метода и применяется в основном при решении задач двумерного...

• Многокритериальная постановка задачи выбора проектов целевых программ - Многокритериальная постановка задачи выбора проектов целевых программ

  В настоящее время Российская Федерация входит в состав ВТО, в связи с чем, для устойчивого развития, для надежности, для стойкости [1, 2] появляется...

• Графическое решение задачи нелинейного программирования - Методика решения двойственных задач линейного программирования

  Так как целевая функция не является линейной, то эта задача является задачей нелинейного программирования. Найдем ее решение, используя геометрическую...

• Некоторые особенности решения задач нелинейного программирования - Экономико-математические методы

  Для решения ЗНП существенно знать: 1) выпукло или не выпукло множество допустимых решений задачи; 2) является ли целевая функция выпуклой или вогнутой...

• Геометрический метод решения задач ЛП - Решение оптимизационных экономических задач методами линейного программирования

  Необходимо найти минимальное значение целевой функции F = 4x1+18x2 > min, при системе ограничений: X1+4x2?14(1) X1+6x2?15(2) X1+x2?5(3)...

• Заключение, Список литературы - Возможности генетических алгоритмов для решения задачи многокритериальной оптимизации инвестиционного портфеля

  С помощью специальных генетических алгоритмов (NSGA, NPGA, MOGA) была решена задача многокритериальной оптимизации инвестиционного портфеля. Каждый из...

• АНАЛИЗ ДЕЯТЕЛЬНОСТИ ПРЕДПРИЯТИЯ - Оптимизация управлением производства на примере ОАО "Днепропетровский стрелочный завод"

  В результате проведенного финансового анализа предприятия можно сделать вывод, что состояние его удовлетворительное, но имеется ряд недостатков: В...

• О разложении в ряд Фурье непериодической функции - Приложение интегрального и дифференциального исчисления к решению прикладных задач

  Пусть на некотором отрезке [a, b] задана кусочно-монотонная функция f(x). Покажем, что данную функцию в точках ее непрерывности можно представить в виде...

• Решение задачи - Основы эконометрики

  Требуется: 1. Построить линейное уравнение парной регрессии y по x. 2. Рассчитать линейный коэффициент парной корреляции, коэффициент детерминации и...

• Особенности постановки и решения общей задачи линейного программирования - Определение оптимальной стратегии рыночного поведения с использованием макроэкономических методов и моделей

  Второй раздел курсовой работы посвящен особенностям постановки и решения общей задачи линейного программирования, а именно, транспортной задаче (ТЗЛП)....

• Понятие производной, Основные правила и формулы дифференцирования, Геометрический смысл производной, Уравнение касательной и нормали к графику функции, угол между ними - Применение производной в решении геометрических задач

  Пусть функция определена в промежутке Х (рис.1). Исходя из некоторого значения независимой переменной, придадим ему приращение, не выводящее его из...

• Оптимальное решение модели. - Методика решения задачи целочисленного программирования

  Рис. 1 Шаг 1. Исходную задачу 1 заносим в дерево задач. В качестве исходного допустимого решения берем: x1=x2=x3=0. Соответствующее значение целевой...

• Решение задачи графическим методом - Математическое моделирование в менеджменте и маркетинге

  Необходимо найти максимальное значение целевой функции L(x)= 2x1+2x2 > max, при системе ограничений: 6x1+8x2?48, (1) 8x1+11x2?88, (2)...

• Изложение теоретических аспектов исследования, Динамическое программирование - Реферативно-прикладное исследование применения экономико-математических методов в решении задач производства (метод нелинейного программирования)

  Динамическое программирование Динамическое программирование -- один из разделов оптимального программирования, в котором процесс принятия решения и...

• Решение геометрических задач на нахождение наибольшего и наименьшего значений с помощью производной, Планиметрические задачи - Применение производной в решении геометрических задач

  Планиметрические задачи Задача 1.Написать уравнения касательной и нормали к графику функциив данной точке, если: [3]. Решение. Уравнение касательной...

• Нелинейное программирование - Реферативно-прикладное исследование применения экономико-математических методов в решении задач производства (метод нелинейного программирования)

  Это раздел математического программирования, изучающий методы решения таких экстремальных задач, в которых результаты (эффективность) возрастают или...

• Общая постановка задачи исследования операций - Экономико-математические методы

  Все факторы, входящие в описание операции, можно разделить на две группы: Постоянные факторы (условия проведения операции), на которые мы влиять не...

• Автоматизированное решение транспортной задачи линейного программирования, Определить количество закупаемого заданным филиалом фирмы сырья у каждого АО, (xj), максимизируя прибыль филиала., С помощью полученных в результате реализации модели отчетов сделать рекомендации филиалу фирмы по расширению программы выпуска ассортимента продукции. - Определение оптимальной стратегии рыночного поведения с использованием макроэкономических методов и моделей

  В разделе 1 курсовой работы требуется: Определить количество закупаемого заданным филиалом фирмы сырья у каждого АО, (xj), максимизируя прибыль филиала....

• Теоремы двойственности и их использование в задачах ЛП - Решение оптимизационных экономических задач методами линейного программирования

  Исходная задача: При ограничениях: Двойственной является следующая задача: При ограничениях: Число неизвестных в двойственной задаче равно 2....

• Введение - Постановка задачи прогнозирования продуктивности агроэкосистем

  В последнее время все чаще возникают трудноформализуемые задачи, то есть такие, для которых алгоритм решения либо не является единственным, либо не...

• Метод равномерной оптимизации, Метод справедливого компромисса, Метод свертывания критериев - Формирование оптимальной производственной программы предприятия

  В этом случае лучшим считается вариант, у которого суммарная величина отдельных целевых функций принимает максимальное значение: F Max = = max...

• Элементы матричного анализа - Методы решения системы линейных уравнений

  Вектором, как на плоскости, так и в пространстве, называется направленный Отрезок , то есть такой Отрезок , один из концов которого выделен и называется...

• Тестовые данные для задачи оптимизации ИП - Возможности генетических алгоритмов для решения задачи многокритериальной оптимизации инвестиционного портфеля

  Инвестиционный портфель оптимальный многокритериальный В качестве тестового примера использовались следующие входные данные [Социальная сеть инвесторов,...

• Постановка задачи, Основные сведения - Комплексное исследование численных методов для задачи решения нелинейных уравнений

  Провести комплексное исследование численных методов для задачи решения нелинейных уравнений. 1. Решить нелинейные уравнения А) ; Б) ; В) . 2....

• Постановка задачи - Методика решения задачи целочисленного программирования

  Сформулировать по заданному 24-хзначному числу модель целочисленного программирования вида: Где все параметры модели должны быть определены из следующих...

• Постановка задачи регрессионного анализа - Основы научных исследований

  Основное назначение Регрессионного анализа (РА) - получение по экспериментальным данным зависимостей, аппроксимирующих эти данные в виде алгебраических...

Постановка задачи многокритериальной оптимизации - Многокритериальная оптимизация на основе нейросетевой, нечеткой и нейро-нечеткой аппроксимации функции предпочтений лица, принимающего решения

Предыдущая | Следующая