Нелинейное программирование - Реферативно-прикладное исследование применения экономико-математических методов в решении задач производства (метод нелинейного программирования)

Это раздел математического программирования, изучающий методы решения таких экстремальных задач, в которых результаты (эффективность) возрастают или убывают не пропорционально изменению масштабов использования ресурсов (или, что то же самое, масштабов производства) из-за деления издержек производства на предприятиях на переменные и условно-постоянные, из-за насыщения спроса на товары, когда каждую следующую единицу продать труднее, чем предыдущую, из-за влияния внешней экономики, внешних издержек и т. д.

Как известно, общая задача математического программирования формулируется следующим образом: найти вектор X = (X1, x2, ..., xN), удовлетворяющий системе ограничений

GI (X1, x2, ..., xN) = BI , i=1,2, ...,k,

(1) GI (X1, x2, ..., xN) ? BI , i=k+1,k+2, ...,m

И доставляющий экстремум функции

(2) Z=f (X1, x2, ..., xN)

При этом предполагается, что известны функции GI (X1, x2, ..., xN) и F (X1, x2, ..., xN) . Обычно на некоторые переменные X1, x2, ..., xN Накладывается условие неотрицательности. Кроме того, ограничением может служить условие целочисленности решения для ряда переменных. Если

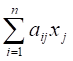
GI (X1, x2, ..., xN) = , i=1,2,...,m,

И

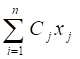
Z=f (x1, x2, ..., xN)=,

Где AIj И СJ - известные константы, то при условии неотрицательности решения получаем задачу линейного программирования. Любую другую задачу математического программирования, не удовлетворяющую условиям (1) и (2) ,будет считаться нелинейной.

Класс задач нелинейного программирования значительно шире класса задач линейного программирования. Основные результаты в нелинейном программировании получены при рассмотрении задач, в которых система ограничений линейная, а целевая функция нелинейная. Даже в таких задачах оптимальное решение может быть найдено только для узкого класса целевых функций. Рассмотрим частные случаи, когда целевая функция сепарабельная или квадратичная.

Если в задачах линейного программирования точки экстремума являются вершинами многогранников решений, то, как следует из рассмотренных ниже примеров, в задачах с нелинейной целевой функцией они могут лежать внутри области, на ребре (грани) или в вершине многогранника. Таким образом, с помощью методов линейного программирования, позволяющих осуществить переход из одной вершины многогранника в другую, можно получить оптимальное решение нелинейных задач при условии, что целевая функция удовлетворяет добавочным ограничениям.

Рассмотрение задач нелинейного программирования начинают с классической задачи оптимизации. Задачи такого рода имеют место, если система (2.1) содержит только уравнения, отсутствуют условия неотрицательности и целочисленности переменных, а функции GI (X1, x2, ..., xN) и F (x1, x2, ..., xN) Непрерывны и имеют частные производные не ниже второго порядка. Классические методы оптимизации при этом являются теоретическим аппаратом, позволяющим в ряде случаев обосновать разработку соответствующего вычислительного метода.

РИС 8

Рассмотрим примеры решения задач нелинейного программирования с двумя переменными. Так же как и в линейном программировании, они могут быть решены графически.

Пример 1. Найти минимальное и максимальное значения сепарабельной функции Z = (X1 -- 4)2 - f - (Х2 -- 6)2 при ограничениях

Х1+х2?1, Х1?0, Х2?0.

2х1+3х2?12,

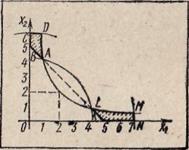
Решение. Область допустимых решений представляет собой много - угольник АВСЕ (рис. 2.1). Если положить Z = Q (Q > 0), то получим уравнение окружности (х1 -- 4)2 + (х2 -- б)2 = Q. С уменьшением (увеличением) Q (квадрата радиуса) значения функции Z соответственно уменьшаются (увеличиваются).

Проводя из точки М Как из центра окружности различных радиусов, получаем: минимальное значение функция Z (D) = 196/13 принимает в точке D (24/13; 36/13), в которой окружность касается области решений. Точка D не является угловой, ее координаты находят в результате решения системы уравнений, соответствующих прямым MD И СЕ.

Функция Z имеет два локальных максимума: А (1;0) функция Z (А) = 45, в вершине Е (6; 0) функция Z (Е) =40. Так как Z(A)>Z(Е) То вершина А -- точка глобального максимума.

Пример 2. Пусть область допустимых решений останется прежней, a Z = = (x1 -- 4)2 + (х2 -- 1)2 . Найти минимальное и максимальное значения этой функции.

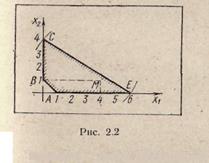
Решение. Минимальное значение функция принимает в точке М (4; 1) (рис. 2.2): Z (М) = 0. Функция Z Имеет два локальных максимума: в вершине Е (6; 0) функция Z (Е) = 5, в вершине С (0; 4) функция Z (С) = 25, причем глобальный максимум достигается в вершине С.

Пример 3. Найти минимальное и максимальное "рачения функции Z = при ограничениях

х1 * х2?4,

х1+ х2?5,

х1 ? 7, Х1 ?0, Х2?0.

х2?6,

Решение. В этом случае (рис. 2.3) область допустимых решений не является выпуклой и состоит из двух отдельных частей. Минимальное значение Функции Z = 17 достигается в точках А (1; 4) и L (4; 1). Функция Z Имеет два локальных максимума: в точке D (2/3; 6) функция Z (D) = 328/9 и в точке М (7; 4/7) функция Z (М) = 2417/49. Точка М Является точкой глобального максимума.

Похожие статьи




Нелинейное программирование - Реферативно-прикладное исследование применения экономико-математических методов в решении задач производства (метод нелинейного программирования)

Предыдущая | Следующая