Теория игр - Реферативно-прикладное исследование применения экономико-математических методов в решении задач производства (метод нелинейного программирования)
При решении экономических задач часто анализировать ситуации, в которых сталкиваются интересы двух или более конкурирующих сторон, преследующих различные цели; это особенно характерно в условиях рыночной экономики. Такого рода ситуации называются Конфликтными.
Математической теорией конфликтных ситуаций является Теория игр. В игре могут сталкиваться интересы двух (Игра парная) или нескольких (Игра множественная) противников; существуют игры с бесконечным множеством игроков. Если во множественной игре игроки образуют коалицию, то игра называется коалиционной; если таких коалиций две, то игра сводится к парной. На промышленных предприятиях теория игр может применяться для выбора оптимальных решений, например, при создании рациональных запасов сырья, материалов, полуфабрикатов, когда противоборствуют две тенденции: увеличение запасов, гарантирующих бесперебойную работу производства, сокращения запасов в целях минимизации затрат на их хранение. В сельском хозяйстве теория игр может применяться при решении таких экономических задач, как посева одной из возможных культур, урожай которой зависит от погоды, если известны цена единицы той или иной культуры и средняя урожайность каждой культуры в зависимости от погоды (например, будет ли лето засушливы, нормальным или дождливым); в этом случае одним выступает сельскохозяйственное предприятие, стремящееся обеспечить наибольший доход, а другим -- природа.
Решение подобных задач требует полной определенности формулировании их условий (Правил игры); установления количества игроков, выявления возможных стратегий игроков, возможных выигрышей (проигрыш понимается как отрицательный выигрыш). Важным элементом в условии игровых задач является Стратегия, т. е. совокупность правил, которые в зависимости от ситуации в игре определяют однозначный выбор действий данного игрока. Если в процессе игры игрок применяет попеременно несколько стратегий, то такая стратегия называется смешанной, а ее элементы -- чистыми стратегиями. Количество стратегий у каждого игрока может быть конечным и бесконечным, в зависимости от этого игры подразделяются на Конечные и Бесконечные.
Важными являются понятия Оптимальной стратегии, Цены игры, среднего выигрыша. Эти понятия находят отражение в определении Решения Игры: стратегии Р* и Q* первого и второго игрока соответственно называются их Оптимальными стратегиями, а число V -- Ценой игры, если для любых стратегий Р первого игрока и любых стратегий Q выполняются неравенства:
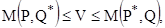
Где М (Р, Q) означает математическое ожидание выигрыши (средней выигрыш) первого игрока, если первым и вторым игроками избраны соответственно стратегии Р и Q.
Из неравенств следует, в частности, что V = M (P*,Q*),т. е. цена игры равна математическому ожиданию выигрыша первого игрока, если оба игрока изберут оптимальные для себя стратегии.
Одним из основных видов игр являются Матричные игры, которыми называются парные игры с Нулевой суммой (один игрок выигрывает столько, сколько проигрывает другой) при условии, что каждый игрок имеет конечное число стратегий. В этом случае парная игра формально задается матрицей А = (аIj), элементы которой аIj определяют выигрыш первого игрока (и соответственно проигрыш второго), если первый игрок выберет i-ю стратегию (i = ), а второй --j-ю стратегию (j = ). Матрица А называется Матрицей игры, или Платежной матрицей.
Существует ряд методов решения матричных игр. Если матрица игры имеет одну из размерностей, равную двум (у одного из игроков имеется только две стратегии), то решение игры может быть получено графически. Известно несколько методов приближенного решения матричной игры, например, метод Брауна. Во многих игровых задачах в сфере экономики неопределенность вызвана не сознательным противодействием противника, а недостаточной осведомленностью об условиях, в которых действуют стороны.
Когда одной из сторон выступает природа, когда неизвестно заранее погода, игры называются - Играми с природой. В этих случаях строки матрицы игры соответствуют стратегии игрока, а столбцы -- состояниям "природы". В ряде случаев при решении такой игры рассматривают Матрицу рисков.
При решении игр с природой используется так же ряд критериев: критерий Сэвиджа, критерий Вальда, критерий Гурвица и др.
При Максимальном критерии Вальда оптимальным считается та стратегия лица, принимающего решение, которая обеспечивает максимум минимального выигрыша; применяя этот критерий, ЛПР в большей степени ориентируется на наихудшие условия (этот критерий иногда называют критерием "крайнего пессимизма").
Критерий Минимаксного риска Сэвиджа Предполагает, что оптимальной является та стратегия, при которой величина риска в наихудшем случае минимальна.
При использовании критерия "пессимизм -- оптимизма" Гурвица ЛПР выбирает некоторый так называемый "коэффициент пессимизма" q; при q = 1 критерий Гурвица приводится к критерию Вальда ("крайнего пессимизма"), а при критерию q=0 "крайнего оптимизма".
Похожие статьи
-
Теория игр исследует оптимальные стратегии в ситуациях игрового характера. К ним относятся ситуации, связанные с выбором наивыгоднейших производственных...
-
Модели теории игр. Основные определения и термины В разных областях целенаправленной деятельности, например при разработке и эксплуатации АСУ, часто...
-
Это раздел математического программирования, изучающий методы решения таких экстремальных задач, в которых результаты (эффективность) возрастают или...
-
Динамическое программирование Динамическое программирование -- один из разделов оптимального программирования, в котором процесс принятия решения и...
-
Модели линейного программирования. Основные определения Еще одним классом задач экономико-математического моделирования являются задачи линейного...
-
Основные понятия и обозначения Динамическое программирование как самостоятельная дисциплина сформировалась в пятидесятых годах двадцатого века. Большой...
-
Для достижения поставленной цели предприятию требуются материалы, оборудование, энергия, рабочая сила и другие ресурсы. Каждое предприятие такими...
-
Из перечисленного обзора типов ММ, составляющих предмет ИСО, можно выделить следующие особенности ММ ИСО [3]. - Системный подход, заставляющий...
-
В начале пятилетнего периода работы предприятию выделена сумма в C руб. для приобретения нового оборудования. Стоимость одного комплекта оборудования...
-
Иногда необходимо управлять сложными комплексами взаимосвязанных работ, направленных на достижение определенных целей. Примерами таких комплексов в...
-
Большое число экономических и планово-производственных задач связано с распределением каких-либо, как правило, ограниченных ресурсов (сырья, рабочей...
-
Комментарии к третьему разделу курсовой работы В третьем разделе курсовой работы студенту предлагается определить оптимальную стратегию заказа в условиях...
-
Необходимость введения нового ограничения может возникнуть, например, когда первоначально для сокращения затрат машинного времени некоторые интуитивно...
-
Вариации коэффициентов целевой функции ЗЛП приводят к изменению направления вектора градиента. Так как при этом не затрагивается допустимое множество, то...
-
Основные понятия теории экономико-математического моделирования Кибернетический подход к исследованию экономико-математических систем Обычно...
-
Важным этапом изучения явлений предметов процессов является их классификация, выступающая как система соподчиненных классов объектов, используемая как...
-
Ограничение чувствительность задача программирование Вариации правых частей ограничений приводят к изменению области допустимых решений ЗЛП, в действии...
-
Изучение теоретических вопросов анализа чувствительности оптимального решения ЗЛП к вариациям некоторых параметров задачи и введению нового ограничения....
-
Объем выпуска продукции Y зависит от количества вложенного труда x как функция . Цена продукции v, зарплата p. Другие издержки не учитываются. Найти...
-
Некоторые особенности решения задач нелинейного программирования - Экономико-математические методы
Для решения ЗНП существенно знать: 1) выпукло или не выпукло множество допустимых решений задачи; 2) является ли целевая функция выпуклой или вогнутой...
-
Любое частное решения уравнения (1) на координатной плоскости х0у изображено в виде графика функции у=у (х, с) (с=const). В теории дифференциальных...
-
Линейное программирование, Общая задача линейного программирования - Экономико-математические методы
Термин "линейное программирование" впервые появился в 1951 г. в работах американских ученых (Дж. Данциг, Т. Купманс), а первые исследования по линейному...
-
Общая постановка задачи исследования операций - Экономико-математические методы
Все факторы, входящие в описание операции, можно разделить на две группы: Постоянные факторы (условия проведения операции), на которые мы влиять не...
-
Системы массового обслуживания -- это такие системы, в которые в случайные моменты времени поступают заявки на обслуживание, при этом поступившие заявки...
-
В разделе 1 курсовой работы требуется: Определить количество закупаемого заданным филиалом фирмы сырья у каждого АО, (xj), максимизируя прибыль филиала....
-
В зависимости от содержания задачи может быть два случая: когда ребра графа G единичной длины; когда ребра графа произвольной длины. Для каждого из этих...
-
Экономико-математические методы и моделирование в землеустройстве позволяют решать большой круг задач, связанных с оптимизацией территориальной...
-
Исходная задача: При ограничениях: Двойственной является следующая задача: При ограничениях: Число неизвестных в двойственной задаче равно 2....
-
Так как целевая функция не является линейной, то эта задача является задачей нелинейного программирования. Найдем ее решение, используя геометрическую...
-
Несмотря на требование линейности функций критериев и ограничений, в рамки линейного программирования попадают многочисленные задачи распределения...
-
Наиболее ранним способом формализации экономико-математических и ТС является представление физических явлений с помощью систем дифференциальных...
-
Тема, с которой мы сегодня ознакомимся это "Применение матриц при решении экономических задач." Рассмотрим как с помощью матриц можно решать...
-
Игра для двух игроков - Шулеры, или Математическое исследование одной карточной игры
Пусть на круге ( N, k ) играют два игрока. Они делают ходы по очереди. Проигрывает тот, кто не может сделать ход. Кто выигрывает при правильной игре?...
-
Постановка задачи - Методика решения задачи целочисленного программирования
Сформулировать по заданному 24-хзначному числу модель целочисленного программирования вида: Где все параметры модели должны быть определены из следующих...
-
Известно оптимальное решение X*=(0;0;1;1) задачи линейного программирования: Составьте двойственную задачу и найдите ее оптимальное решение по теореме...
-
Календарный производственный программирование однооперационный Все существующие методы решения задач календарного планирования3 по степени достижения...
-
Математическая модель задачи нелинейного программирования (ЗНП) (*) Для ЗНП в отличие от Задачи Линейного Программирования (ЗЛП) нет единого метода...
-
Введение - Решение оптимизационных экономических задач методами линейного программирования
Линейное программирование является составной частью раздела математики, который изучает методы нахождения условного экстремума функции многих переменных...
-
Основные понятия сетевых и графовых моделей Объектом исследования является сеть, состоящая из узлов и линий связи. Предполагается, что в сети имеется два...
-
Как известно решение задач симплексным методом применяется очень часто. Это связано с тем, что симплексный метод подходит для решения широкого круга...
Теория игр - Реферативно-прикладное исследование применения экономико-математических методов в решении задач производства (метод нелинейного программирования)