Конечные прямые и подпрямые произведения - Формационные основы универсальных алгебр
На протяжении всего параграфа будут рассматриваться только конечные проиведения.
Пусть алгебра и - подалгебра алгебры. Тогда отображение
Такое, что для любого элемента
,
Называется Проектированием в, элемент называется -- компонентой или простой - ой компонентой элемента.
Проектирование является гомоморфизмом в. Действительно, для любых элементов
И любой - арной операции имеем
Подалгебра алгебры называется Проекцией подалгебры в.
Подалгебра алгебры называется Подпрямым произведением алгебр, если проекция в совпадает с для любого.
6.1. Теорема. Пусть -- конгруэнции на алгебре и
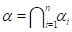
.
Тогда фактор алгебра Изоморфна подпрямому произведению
Доказательство. Пусть -- отображение из в произведение (1) такое, что
.
Для любых элементов и любой - арной операции имеем
Следовательно, - гомоморфизм на алгебру (1).
Пусть, тогда
Отсюда следует, что для любого. Значит. Теперь, по первой теореме об изоморфизмах, получаем, что фактор алгебра изоморфна подпрямому произведению (1).
Теорема доказана.
6.2. Теорема. Пусть алгебра представима в виде подпрямого произведения и =Ker, где - проектирование для любого. Тогда
Если же , то
_i
Доказательство.
Для произвольного элемента
Класс эквивалентности представляет собой множество вида
,
Где -- все возможные последовательности элементов из прямого произведения
Отсюда следует, что, т. е. .
Пусть. Очевидно, достаточно показать, например, что для
Выполняется равенство
Действительно, для любого элемента, где
Имеем
и
Следовательно, Аналогичным образом из
и
Следует, что. Теперь из 1) следует попарная перестановочность конгруэнций.
Теорема доказана.
- 6.3. Алгебра называется Подпрямо неразложимой, если в любом представлении алгебры в виде подпрямого произведения алгебр, , хотя бы одна из операций проектирования является изоморфизмом. 6.4. Теорема. Конечная алгебра подпрямо неразложима тогда и только тогда, когда любое конечное пересечение всех ее ненулевых конгруэнций является ненулевой конгруэнцией.
Доказательство.
Пусть алгебра подпрямо неразложима и пересечение всех ее ненулевых конгруэнций является нулевой конгруэнцией. Тогда по теореме 6.1. изоморфна подпрямому произведению вида (1). Противоречие.
Обратно, пусть пересечение всех ненулевых конгруэнций алгебры есть ненулевая конгруэнция и подпрямо разложима. Тогда в силу теоремы 6.2.
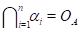
,
Где - проектирование. Противоречие.
Тем самым теорема доказана.
Заметим, что из теоремы 6.4. , например, вытекает подпрямая неразложимость конечных групп, содержащих наименьшую ненулевую нормальную подгруппу (в частности, конечных абелевых групп порядка, где - простое число).
Похожие статьи
-
Решетка конгруэнций - Формационные основы универсальных алгебр
Если - отношение эквивалентности на множестве и, то будем это отношение изображать в виде неориентированного графа Ris04.eps Ris05.eps 4.1. Теорема....
-
Гомоморфизм алгебр. Конгруэнции - Формационные основы универсальных алгебр
3.1. Отображение f из алгебры A в алгебру B называется гомоморфизмом, если для любых элементов и любой n-арной операции справедливо равенство Если же...
-
Многообразия - Формационные основы универсальных алгебр
8.1. Пусть и -- слова сигнатуры в счетном алфавите. Тогда формальное равенство называется - тождеством или тождеством сигнатуры. Пусть тождество имеет...
-
Ряды конгруэнций - Формационные основы универсальных алгебр
5.1. Конечная цепь конгруэнции алгебры А вида (1) , Называется Рядом конгруэнций, а число -- Длиной ряда. Фактор алгебры называется Главным , если и из ,...
-
Алгебры слов (термов) - Формационные основы универсальных алгебр
7.1. Пусть - некоторая сигнатура, - произвольное множество, в частности пустое. Построим множество - слов (- термов) индуктивно следующим образом:...
-
Решетки (структуры) - Формационные основы универсальных алгебр
Понятие решетки (пример 11) играет исключительно важную роль в изучении самых общих алгебр. И это, в первую очередь, связано с иным подходом в...
-
Определение. Примеры - Формационные основы универсальных алгебр
1. Пусть А - непустое множество (АШ), n -- натуральное число, - декартова (прямая) n-ая степень множества А. В частности, если n=0, то под будем понимать...
-
Введение - Формационные основы универсальных алгебр
Впервые, понятие формации алгебраических систем было введено Л. А. Шеметковым в 1984 г. в работе [1] .Напомним, что непустой класс F алгебраических...
-
Актуальность исследования Цель исследования: Изучение теоретических и практических аспектов евклидовости в математике Задачи исследования: 1. Изучить...
-
В школьной алгебре одночленом от некоторой буквы x называется алгебраическое выражение вида, где a - некоторое число, x - буква, m - целое...
-
Все накопленные веками знания о природе, систематизированы, логически предельно развиты в первой универсальной картине мира, которую создал в IV в. до н....
-
Теорема об универсальной функции - Рекурсивные функции
Для любого n, nN, универсальная функция u(n) вычислима. Доказательство. При доказательстве мы можем ограничиться случаем N=1. Действительно, программу,...
-
Следом плоскости называется линия пересечения плоскости с плоскостями проекций. В зависимости от того с какой из плоскостей проекций пересекается данная,...
-
Прямые линии в пространстве могут быть параллельными, пересекающимися и скрещивающимися. Рассмотрим подробнее каждый случай: 1. Параллельные прямые...
-
Плоскость геометрический точка проецирование Длину отрезка АВ можно определить из прямоугольного треугольника АВС-- AС = A1B1...
-
В зависимости от положения прямой по отношению к плоскостям проекций она может занимать как общее, так и частные положения. 1. Прямая не параллельная ни...
-
Матрицы над евклидовым кольцом - Евклидовость в математике
Введем следующее определение: строку над евклидовым кольцом Е будем называть канонической, если, кроме главного элемента, все остальные ее элементы...
-
Принцип универсального эволюционизма - Основы естественно-научных знаний
Все существует в развитии. Развитие - это есть чередование медленных количественных и быстрых качественных изменений. Законы природы по существу есть...
-
II семестр §1. Евклидово пространство Евклидово пространство - это линейное пространство с некоторым образом введенной операцией "скалярного...
-
Евклидовы кольца - Евклидовость в математике
Кольцо целостности Е называется евклидовым, если на множестве Е можно определить функцию е, значение которой является целыми неотрицательными числами,...
-
Моделирование в условиях противодействия, игровые модели - Основы теории систем и системного анализа
Как уже неоднократно отмечалось, системный анализ невозможен без учета взаимодействий данной системы с внешней средой. Ранее упоминалась необходимость...
-
Обозначения: Длина вектора, модуль (абсолютная величина): Сумма векторов: (правило треугольника) (рис. 1.22); (правило параллелограмма) (рис. 1.23);...
-
СКАЛЯРНОЕ ПРОИЗВЕДЕНИЕ ВЕКТОРОВ Скалярным произведением двух векторов иназывается число S =|| || сos (). Эта операция обозначается. В частности,...
-
Статистики, Свойства оценок - Основы научных исследований
Любая функция от элементов выборки называется Статистикой . Следовательно, точечная оценка также является статистикой. Однако не всякая статистика может...
-
Показатели вариации - Основы эконометрики
Показатели вариации делятся на две группы: абсолютные и относительные. К Абсолютным показателям вариации относятся: § размах вариации; § среднее линейное...
-
Методы отбора выборок - Основы научных исследований
Известны три метода отборок выборок: случайный, систематический и комбинированный. В результате случайного отбора получается случайная выборка. Выборка...
-
Теорема о параметризации., Универсальные функции - Рекурсивные функции
Любую часть x1,x2,...,xn входных значений можно породить программно, более того - существует алгоритм, который генерирует по x1,x2,...,xn текст...
-
Лемма (о декартовом произведении)., Замечания и упражнения - Рекурсивные функции
Если А - эффективное множество, то Для любого эффективного множества B AB эффективно (и, следовательно, любое декартово произведение A1A2...Аn...
-
Теоретические основы масс-спектрометрии Масс-спектрометрия представляет собой метод исследования веществ, основанный на определении массы (точнее,...
-
Пусть по окружности в некотором порядке расположены N единиц и нулей (исходное состояние S 0). Некоторые нули разрешается заменять на единицы в...
-
В данной главе описан способ прогнозирования с помощью НС, основанный на методе окон. Также приведен обзор применения НС в финансовой сфере. Общий подход...
-
Генеральная совокупность и выборка - Основы научных исследований
Распределение случайной величины содержит всю информацию о ее статистических свойствах. Много ли нужно знать значений случайной величины, чтобы построить...
-
А) Углерод (С), кремний (Si), германий (Ge), олово (Sn), свинец (РЬ) - элементы 4 группы главной подгруппы ПСЭ. На внешнем электронном слое атомы этих...
-
Теорема 1. Предел постоянной равен самой постоянной. . Доказательство. f(x)=с, докажем, что . Возьмем произвольное e>0. В качестве d можно взять любое...
-
Дуэль с бесконечностью - Великая теорема Ферма
Чтобы доказать Великую теорему Ферма, Уайлсу было необходимо сначала доказать гипотезу Таниямы-Шимуры о том, что каждой эллиптической кривой можно...
-
Сравнение множеств Определение. Множества A и B называются равномощными, если между A и B существует взаимно однозначное соответствие. Утверждение....
-
Производной. - Методы решения системы линейных уравнений
Наиболее просто основные теоремы дифференциального исчисления формулируются для гладких функций. [ Править ] Производные и гладкие функции Пусть функция...
-
Линейная функция - Конформное отображение
Определение 2. Функция вида: , где - фиксированные комплексные числа, называется линейной. Определение 3. Отображение, осуществимое линейной функцией...
-
1. Пусть интегрируемая на сегменте функция неотрицательна на этом сегменте. Тогда: . 2. Если функция интегрируемая на сегменте и, то: . 3. Если функция...
-
Теорема: Непрерывная на сегменте функция интегрируема на этом сегменте. Теорема: Если функция определена и ограничена на сегменте, и если для любого...
Конечные прямые и подпрямые произведения - Формационные основы универсальных алгебр