Сравнение множеств
Сравнение множеств
Определение. Множества A и B называются равномощными, если между A и B существует взаимно однозначное соответствие.
Утверждение. Отношение равномощности множеств является отношением эквивалентности.
Доказательство.
- 1) Рефлективность можно установить, отображая множество само на себя с помощью функции f(x)=x. То есть A=A. 2) Симметричность. Если:
- - взаимно однозначное соответствие, то и: - также взаимно однозначное соответствие.
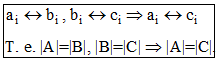
Рассмотрим разные случаи.
Случай 1. A и B конечны.
Утверждение. В случае, когда A и B конечны A и B равномощны тогда и только тогда, когда количество элементов A = количеству элементов B.
Доказательство:
A) Если количество элементов одинаково, то перенумеруем их и установим взаимно однозначное соответствие:
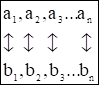
Следовательно, множества равномощны.
Б) Пусть множества A и B равномощны. Тогда существует взаимно однозначное соответствие между элементами A и B. Следовательно, их количество должно быть одинаковым.
Поэтому для конечных множеств A можно принять, что мощность |A|=количеству элементов A.
Случай 2. Бесконечные множества.
Мощность целого может равняться мощности части. Рассмотрим множества
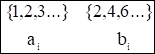
Можно установить соответствие: . Следовательно, множества равномощны.
Определение. Говорят, что мощность множества A не превосходит мощности множества B (пишут ), если множество:
В частности, если AB, то B1=A.
Определение. Говорят что A меньше B (), если:
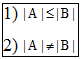
Теорема. Отношение на совокупности множеств есть отношение частичного порядка для мощностей множеств.
- 1) Рефлективность: 2) Транзитивность:
Существуют подмножества отображения такие, что:
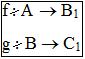
Тогда f - соответствие между A и каким-то подмножеством C.
3) Анти симметричность:
Теорема - отношения линейного порядка (без док-ва).
Теорема Кантора. Пусть N - множество натуральных чисел, A=[0,1] - отрезок действительной оси. Тогда N<A.
Доказательство.
Любое число из A можно представить в виде бесконечной десятичной дроби:

Построим число b следующим образом:
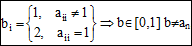
- поскольку b отличается от aN в n-ном знаке.
Приходим к противоречию. Теорема доказана.
Счетные множества
Определение. Множество, равномощное множеству натуральных чисел называется счетным.
Примеры.
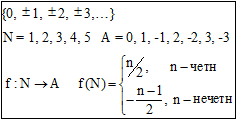
Теоремы о счетных множествах.
Теорема 1. множество содержит счетное подмножество.
Выберем элемент a1A.
A не пусто, так как оно бесконечно.
Выберем элемент {a1} не пусто, так как A бесконечно.
В результате получим множество, каждому элементу которого сопоставлено натуральное число n.
Доказательство.
Пусть:
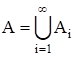

Расположим элементы A в следующем порядке
A11, a12, a21, a31, a22, a13, a14, a23, a32, a41.
Тем самым, получили взаимно однозначное отображение N на A.
Если в множествах A1, A2, A3,... есть общие элементы, то их объединение A есть подмножество рассмотренной выше последовательности.
Следствие 1. Если A и B счетные, то A x B - счетное.
Следствие 2. множество рациональных чисел - счетное:
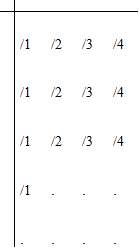
Следующая теорема позволяет утверждать, что не существует "самого большого" по мощности множества.
Теорема. Мощность булеана множества всегда больше мощности самого множества, т. е.:
Возможны ситуации, когда f(x).
Выделим множество:
Приведем это заключение к противоречию. Возможны два случая: либо yP, либо yP.
Пусть yP. Тогда по определению P yP. Противоречие.
Пусть yP. Поскольку в P входят все эл-ты xf(x), то yP. Опять противоречие.
Теорема доказана.
Теорема. Мощность булеана (множества-степени) счетного множества = мощности континуума:
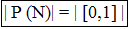
Доказательство.
Пусть 0,010...1... - запись любого числа из A=[0,1] в 2Ой системе счисления.
Сопоставим этому числу подмножество N, состоящее из чисел, равных номерам разрядов, в которых записана единица. Этим устанавливается взаимно однозначное соответствие между B(N) и [0,1].
Примеры. математический теорема число
Установить равномощность или не равномощность множеств:
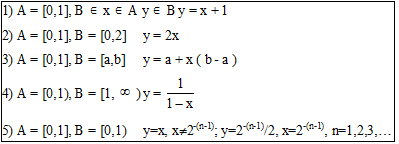
Похожие статьи
-
Пусть: A = 0,4/ x1 + 0,2/ x2+0/ x3+1/ x4; B = 0,7/ x1+0,9/ x2+0,1/ x3+1/ x4; C = 0,1/ x1+1/ x2+0,2/ x3+0,9/ x4. Здесь: 1. A?B, то есть A содержится в...
-
Основные характеристики нечетких множеств, Примеры нечетких множеств - Нечеткая логика
Пусть M = [0,1] и A - нечеткое множество с элементами из универсального множества E и множеством принадлежностей M - Величина ?A(x) называется...
-
Счетные и несчетные множества - Методы решения системы линейных уравнений
Пусть, например, А и В Ї некоторые множества. Тогда их возможные взаимоотношения можно рассмотреть в виде таблицы: Диаграмма Венна Диаграмма Венна...
-
На уровне общества для описания поведения потребителей вводится целевая функция потребления. Целевая функция потребления - функция, выражающая уровень...
-
Операции над нечеткими множествами - Нечеткая логика
Содержание Пусть A и B - нечеткие множества на универсальном множестве E. Говорят, что A содержится в B, если ?x ?E ?A(x) <?B(x)....
-
Нечеткими высказываниями будем называть высказывания следующего вида: 1. Высказывание , где ? - имя лингвистической переменной, ?' - ее значение,...
-
Методы построения функций принадлежности нечетких множеств - Нечеткая логика
В приведенных выше примерах использованы прямые методы, когда эксперт или просто задает для любого x?E значение ?A(x), или определяет функцию...
-
Теперь, когда в рамках данного исследования была получена модель с наилучшими характеристиками для непубличных строительных компаний, полученные...
-
Задача кластеризации реализуется набором методов (алгоритмов), каждый из которых осуществляет разбиения региона на компактные зоны обслуживания. Аппарат...
-
Спрос бюджетный множество потребитель Для индивидуального потребителя может быть сформулирована задача оптимизации выбора. Потребитель, имея доход,...
-
Правило произведения, Пересекающиеся множества - Правила комбинаторики
Если элемент X можно выбрать k способами, а элемент Y-m способами, то пару (X, Y) можно выбрать k*m способами. То есть, если на первой полке стоит 5...
-
Вычисления для следующих входных данных F=1000H m=200 кг m'=1 кг/сек k=2 t0=0 сек V0=0 м/сек B=50 n=50 V1 (t) - результаты, полученные с помощью...
-
При анализе больших объемов данных зачастую их можно представить в виде графа. Основными атрибутами графа являются вершины и ребра, поэтому изучение...
-
В основе метода площадей лежит предположение, что объект может быть описан линейным дифференциальным уравнением с постоянными коэффициентами, а его...
-
Получение кристаллического йода Собрать установку. На асбестированную сетку поставить стакан, в который поместить по 0,5 г измельченных иодида калия и...
-
Сравнение старой и новой парадигм - О новой парадигме математических методов исследования
Проведем развернутое сравнение старой и новой парадигм математических методов исследования. При этом опираемся на материалы раздела "Математические...
-
По итогам проведенного исследования можно прийти к выводу о том, что и логит-регрессия и деревья решений позволили построить модели, которые с...
-
Исходные данные для индексного анализа по хозяйствам приведены в таблице 2.1. Таблица 2.1 Исходные данные для индексного анализа Наименование хозяйств...
-
Уровень жизни - многогранное явление, которое зависит от множества разнообразных причин, начиная от территории, где проживает население, то есть...
-
Выбор наиболее рационального варианта электрической сети осуществляется путем сопоставления технико-экономических параметров вариантов....
-
Наиболее важным применением теории нечетких множеств являются контроллеры нечеткой логики. Их функционирование несколько отличается от работы обычных...
-
Техника оценки стоимости денег во времени позволяет решить ряд важных задач сравнительного анализа альтернативных возможностей вложения денег. Рассмотрим...
-
Сравнение методов получения хлорида калия - Производство хлорида калия галургическим способом
Флотационный метод обогащения по сравнению с галургическим (растворение и кристаллизация) имеет следующие преимущества: - флотация проходит при...
-
Метод сравнения является универсальным методом и применяется во всех разделах статистики (метод сравнения средних, оценивания неизвестных параметров и...
-
Основной целью исследования является сравнение предсказательной силы моделей, построенных на основе различных методов. В условиях несбалансированности...
-
Функции и ее свойства - Методы решения системы линейных уравнений
В современной математике понятие множества является одним из основных. Универсальность этого понятия в том, что под него можно подвести любую...
-
Решетка конгруэнций - Формационные основы универсальных алгебр
Если - отношение эквивалентности на множестве и, то будем это отношение изображать в виде неориентированного графа Ris04.eps Ris05.eps 4.1. Теорема....
-
Линейная функция - Конформное отображение
Определение 2. Функция вида: , где - фиксированные комплексные числа, называется линейной. Определение 3. Отображение, осуществимое линейной функцией...
-
Алгебры слов (термов) - Формационные основы универсальных алгебр
7.1. Пусть - некоторая сигнатура, - произвольное множество, в частности пустое. Построим множество - слов (- термов) индуктивно следующим образом:...
-
Гомоморфизм алгебр. Конгруэнции - Формационные основы универсальных алгебр
3.1. Отображение f из алгебры A в алгебру B называется гомоморфизмом, если для любых элементов и любой n-арной операции справедливо равенство Если же...
-
Теорема 1. Предел постоянной равен самой постоянной. . Доказательство. f(x)=с, докажем, что . Возьмем произвольное e>0. В качестве d можно взять любое...
-
ПРАВИЛО ЛОПИТАЛЯ - Скалярные и векторные величины, матрицы и функции
Теорема Коши. Если при соблюдении предположений относительно функций и отношение стремится к некоторому числу при, то тогда к такому же числу будет...
-
МАТРИЦЫ И ОПЕРАЦИИ НАД НИМИ Матрицей A называется любая прямоугольная таблица, составленная из чисел, которые называют элементами матрицы и обозначается...
-
II семестр §1. Евклидово пространство Евклидово пространство - это линейное пространство с некоторым образом введенной операцией "скалярного...
-
О квази-клике. - Использование квази-клик для анализа графа рынка России
Квази-клика - представляет собой релаксацию строгого условия полноты клики, то есть допускается отсутствие некоторых ребер в искомом подграфе. На данный...
-
Теорема: Непрерывная на сегменте функция интегрируема на этом сегменте. Теорема: Если функция определена и ограничена на сегменте, и если для любого...
-
Теорема: Для того, чтобы ограниченная на сегменте функция была интегрируемой на этом сегменте, необходимо и достаточно, чтобы для любого нашлось такое...
-
Принцип сходимости, Предел функции. Теорема Гейне - Свойства функций
Рассмотрим вопрос о существовании пределов последовательностей концевых точек бесконечной системы промежутков, вложенных друг в друга. Лемма Кантора ....
-
Понятие числовой последовательности - Свойства функций
Числовой последовательностью называется числовая функция, определенная на множестве натуральных чисел . Если функцию задать на множестве натуральных...
-
В школьной алгебре одночленом от некоторой буквы x называется алгебраическое выражение вида, где a - некоторое число, x - буква, m - целое...
Сравнение множеств