Евклидово пространство
II семестр
§1. Евклидово пространство
Евклидово пространство - это линейное пространство с некоторым образом введенной операцией "скалярного произведения".
Определение 1. Линейное пространство над полем вещественных чисел R называется евклидовым пространством, если определено правило, ставящее им в соответствие вещественное число, называемое скалярным произведением и, обозначаемое, и удовлетворяющее следующим аксиомам:
- 1) коммутативность: выполняется ; 2) дистрибутивность: выполняется ; 3) и выполняется ; 4) выполняется, причем
Примеры.
- 1) Множество векторов в с обычным образом определенным скалярным произведением векторов (см. свойства скалярного произведения) образует евклидово пространство. 2) Множество непрерывных на отрезке функций образует евклидово пространство, если скалярное произведение задается формулой:
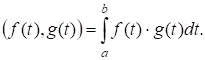
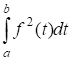
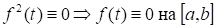
Свойство 1) скалярного произведения очевидно, 2) и 3) следуют из линейности интеграла, 4) следует из того, что от неотрицательной функции неотрицателен и равен нулю только если.
3) Пространство упорядоченных вещественных чисел образует евклидово пространство со скалярным произведением, задаваемым следующей формулой:
Если и из, то
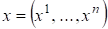
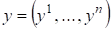
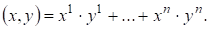
(1)
Евклидово пространство линейный вектор
Свойство 1) ? очевидно, свойства 2) и 3) следуют из определения сложения векторов в и умножения на число, т. е.
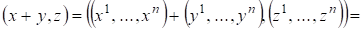
;
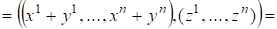
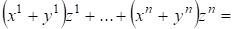
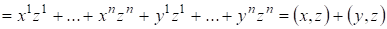
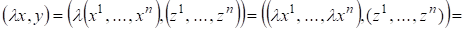
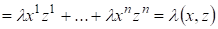
.
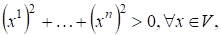
Свойство 4) следует из того, что и равно нулю лишь тогда когда, т. е. .
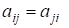
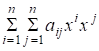
4) Пусть ? матрица над и пусть - симметричная, т. е. . Для любого используем для построения выражения. Такое выражение называется квадратичной формой. Будем предполагать, что такая форма положительно определена, т. е. она больше нуля и равна нулю лишь если.
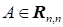
Такую матрицу можно использовать для задания скалярного произведения в следующим образом: ,
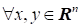
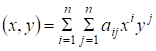
.(2)
Свойство 1) следует из симметричности матрицы, 2) и 3) ? из свойств вещественных чисел, 4) ? из положительной определенности соответствующей квадратичной формы.
Замечание. Формула (1) из (2) при ? единичная матрица.
Теорема 1 (неравенство Коши-Буняковского). Для любых элементов евклидового пространства справедливо неравенство:
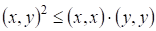
.(3)
Неравенство (3) называется неравенством Коши-Буняковского.
Доказательство: По аксиоме 4) евклидова пространства справедливо
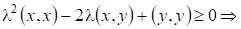
//так как квадратный трехчлен по неотрицателен дискриминант //
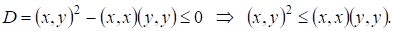
¦
Определение 2. Линейное пространство называется нормированным, если определено правило, по которому ставится в соответствие вещественное число, называемое нормой (или длиной) указанного элемента и обозначаемое, удовлетворяющее следующим трем аксиомам:
- 1) . 2) . 3) справедливо (неравенство треугольника или неравенство Минковского).
Теорема 2. Всякое евклидово пространство является нормированным, если в нем норму элемента определить равенством
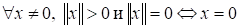
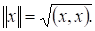
Доказательство: Проверим свойства нормированного пространства: аксиома 1) следует из 4) евклидова пространства, 2) следует из аксиом 1) и 3) евклидова пространства, 3) следует из неравенства Коши-Буняковского. Действительно,
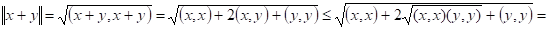
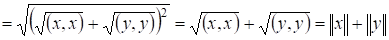
. ¦
Примеры.
1) В пространстве геометрических векторов с обычным скалярным произведением неравенства Коши-Буняковского и Минковского имеют вид:
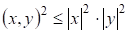
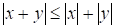
,.
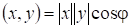

Первое неравенство в силу означает, что, второе ? что длина стороны треугольника не превосходят суммы длин двух других сторон.
2) В неравенства Коши-Буняковского и Минковского дают:
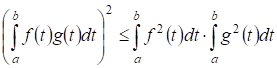
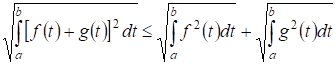
.
3) В с обычным скалярным произведением и имеем
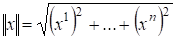
Неравенство Коши-Буняковского
;
Неравенство Минковского
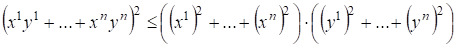
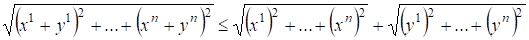
.
4) В со скалярным произведением с положительно определенной симметрической матрицей имеем
Неравенство Коши-Буняковского
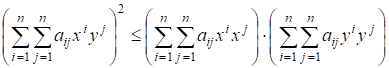
;
Неравенство Минковского
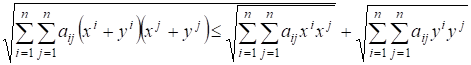
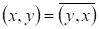
.
Замечание. Если векторное пространство дано над полем, то аналогично строится теория унитарных (или эрмитовых) пространств. В этом случае аксиомы 1) и 4) принимают соответственно вид:
- 1) , 4) и, если.
Отметим, что неравенство Коши-Буняковского в этом случае принимает вид:
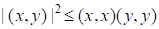
.
В - мерном комплексном координатном пространстве C стандартное скалярное произведение векторов C задается формулой
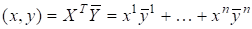
.
Ортогональные и ортонормированные системы векторов
Из неравенства Коши-Буняковского следует, что корректно можно ввести следующее
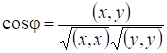
Определение 3. Для любых принадлежащих евклидовому пространству определен угол между ними: .
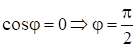
Определение 4. Элементы называются ортогональными, если их скалярное произведение равно нулю, то есть. Тогда.
Очевидно, что если ортогонален, то ортогонален.
Лемма 1. Нулевой вектор ортогонален любому вектору из и является единственным вектором, обладающим этим свойством.
Доказательство самостоятельно.
Определение 5. Сумму двух ортогональных векторов назовем гипотенузой треугольника, построенного на векторах.
Лемма 2. Квадрат гипотенузы равен сумме квадратов катетов.
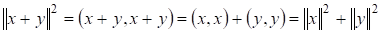
Доказательство: .¦
Обобщение. Если ? взаимно ортогональны
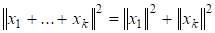
.
Определение 6. Система векторов евклидова пространства называется ортогональной, если она либо состоит из одного вектора, либо ее векторы попарно ортогональны.
Теорема 3. Всякая ортогональная система ненулевых векторов евклидова пространства является линейно независимой.
Доказательство: Пусть ? ортогональная система векторов и пусть
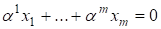
С некоторыми постоянными.
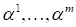
Умножая это равенство скалярно на, получаем
Т. к.
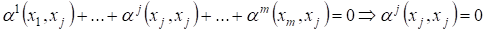
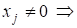
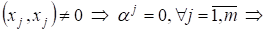
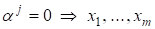
все ? линейно независимы. ¦
Определение 7. Ортогональная система, состоящая из векторов единичной длины, называется ортонормированной.
Определение 8. В - мерном евклидовом пространстве система ортонормированных векторов образует ортонормированный базис.
Теорема 4. Во всяком - мерном евклидовом пространстве существует ортонормированный базис.
Доказательство: Т. к. пространство ? - мерное, то существуют векторов, которые линейно независимы. Покажем, что можно построить и векторы, получающиеся как линейные комбинации, которые образуют ортонормированный базис. Доказательство методом математической индукции:
Если ? очевидно, т. к.
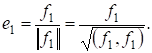
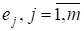
Пусть удалось построить векторов, которые попарно ортогональны, их нормы равны единице, и получены как линейные комбинации. Будем искать вектор. Выберем так, чтобы был ортогонален. Умножая скалярно на, в силу ортонормированности имеем:
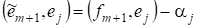
//т. к. //
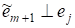
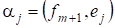
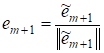
Очевидно, что полученный, т. к. он является линейной комбинацией система ? ортонормированная и получена как линейная комбинация. ¦
Замечание 1. В доказательстве теоремы 4 использовался следующий алгоритм ортогонализации системы векторов, известный как алгоритм Грамма-Шмидта:
Пусть ? линейно независимы. Тогда попарно ортогональные единичные вектора получаются по следующим формулам:
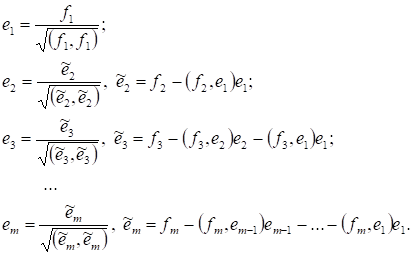
Замечание 2. В любом евклидовом пространстве можно построить много ортонормированных базисов. Примером ортонормированного базиса в с обычным скалярным произведением могут служить вектора
Рассмотрим произвольный ортонормированный базис - мерного евклидова пространства. Пусть ? произвольный вектор и

.
Умножая обе части равенства скалярно на получим:
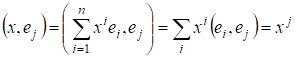
,
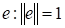
Т. е. координаты произвольного вектора относительно ортонормированного базиса равны скалярным произведениям этого вектора на соответствующие базисные векторы. Поскольку скалярное произведение на вектор, естественно назвать проекцией на, то, следовательно, координаты произвольного относительно ортонормированного базиса равны проекциям этого элемента на соответствующие базисные элементы.
Таким образом, ортонормированный базис похож на декартовый прямоугольный базис.
3. Выражение скалярного произведения через компоненты сомножителей. Матрица Грама.
Пусть в произвольном евклидовом пространстве задан базис. Это позволяет представить в виде
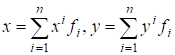
. Вычислим скалярное произведение :
.
Отсюда следует, что если базис ? ортонормированный, то есть
, то
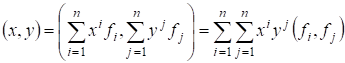
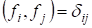
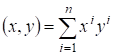
.
Теорема 5. В ортонормированном базисе скалярное произведение любых двух векторов равно сумме произведений соответствующих координат этих векторов.
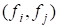
Если же базис {} ? произвольный, то произведения обозначим и введем в рассмотрение квадратную матрицу
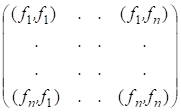
= = ,
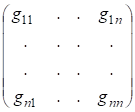
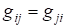
Называемую матрицей Грамма базиса {}. В силу коммутативности скалярного произведения, т. е. матрица Грама симметрическая.
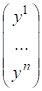
Обозначим = , . Тогда скалярное произведение можно переписать в матричном виде:
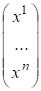
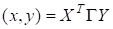
.
Если {} ? ортонормированный, то и.
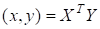
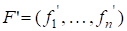
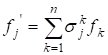
Рассмотрим два базиса {} и {}, связанные при помощи матрицы перехода : если и, т. е. . Тогда для базиса {} матрица Грама имеет вид:
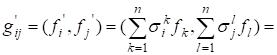
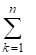
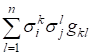
.(5)
Эта формула дает связь между матрицами Грама для двух связанных между собой базисов. Равенство (5) в матричном виде имеет вид:
Что легко проверить прямыми вычислениями.
Рассмотрим последнюю формулу в частном случае, когда {} - ортонормированный. Тогда и формула (6) имеет вид:
Г =
вычисляя определитель в силу теоремы об определителе произведения матриц, имеем:
DetГ= det() det = (det).
Так как {} - произвольный базис // т. к. det0 //
Теорема 6. Определитель матрицы Грама любого базиса положителен.
Эта теорема может быть усилена:
Теорема 7. Пусть,..., ? произвольные (не обязательно линейно независимые) вектора в евклидовом пространстве. Тогда определитель матрицы
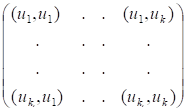
,
Составленной из попарных скалярных произведений, положителен, если вектора линейно независимы, и равен нулю, если они линейно зависимы.
Доказательство: Первое утверждение теоремы следует из теоремы 6, т. к. если,..., ? линейно независимы, то они образуют базис в своей линейной оболочке.
Докажем второе утверждение. Если векторы - линейно зависимы, то выполнено равенство, где хотя бы одно. Умножая это равенство скалярно на каждый из векторов получим систему уравнений
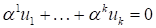
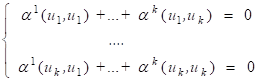
,
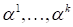
Которой удовлетворяет ненулевое решение определитель матрицы этой системы равен нулю.¦
Замечание. Доказанная теорема обобщает неравенство Коши-Буняковского, которое имеет место при.
Ортогональное дополнение к линейному подпространству.
Определение 9. Два множества и векторов евклидова пространства называются ортогональными, если каждый вектор первого множества ортогонален к каждому вектору второго.
В частности, будем говорить, что вектор ортогонален к множеству, если ортогонален каждому.
Ортогональность и обозначается.
Лемма 3. Если два множества и ортогональны, то их пересечение либо пусто, либо состоит только из нулевого вектора.
Доказательство: На самом деле, если и. ¦
Следствие. Сумма ортогональных подпространств всегда является прямой суммой.
Доказательство:Это следует из того, что их пересечение в силу леммы 3 состоит только из нулевого вектора сумма прямая. ¦
Пусть - подпространство евклидового пространства.
Определение 10. Ортогональным дополнением подпространства E называется множество всех векторов, перпендикулярных каждому вектору из.
Ортогональное дополнение к обозначается.
Очевидно, что - линейное подпространство; на самом деле, если, а, то (u+v, w) = (u, w)+ (v, w) = О u + v U, что и требовалось доказать.
Теорема 8. Евклидово пространство есть прямая сумма любого своего подпространства U и его ортогонального дополнения U.
Доказательство: Пусть dimU=k и пусть e,..., e ? ортонормированный базис в U. В силу теоремы 7 из параграфа 11 (Часть 1) эти вектора можно дополнить до базиса во всем пространстве. Применяя к ним процесс ортогонализации Грама-Шмидта, получим ортонормированный базис e,..., e евклидова пространства.
Любой элемент хЕ может быть разложен по этому базису:
X = xe+...+ xe+ xe+... +xe,
Т. е. х=x+x, где x = xe+...+ xeU, а x = xe+... +xeU,
В силу ортонормированности базиса. Следовательно, в силу следствия к лемме 3, сумма U и U - прямая сумма. ¦
Следствие 1. (U) = U.
Следствие 2. может быть единственным образом представлен в виде х= x+x, где xU, xU. При этом x называется ортогональной проекцией вектора на подпространство U, а x ? ортогональной составляющей относительно U.
Задача. В Е подпространство U натянуто на векторы =(1,0,1,1), и =(0,1,1,-1). Найти ортогональную проекцию и ортогональную составляющую вектора =(1,2,0,1) на подпространство U.
Решение. 1 способ. Вектора и ? ортогональны. Нормируя их, получаем:
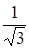
= (1;0;1;1); = (0;1;1;-1). Если = x+x+ x+x, то
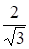
X = (,) = ; x = (,) = Если x = x+x
X = x+x = (;;1;). ;;-1;).
2 способ. Применим процесс ортогонализации к базису в : .
Выберем = (0;0;1;0), = (0;0;0;1) ортогонализация дает:
= - (,e)e - (,e) e = (-;-;;0)
= (-;-;;0). Аналогично, = (-;;0;).
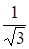
Решим систему:
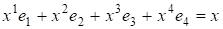
X=, x=, x=-, x= x=x+x; x=x+x.
Похожие статьи
-
Уравнение динамики теплообменника: Передаточные функции объекта получим по его уравнению динамики. Для этого запишем уравнение по заданному каналу. Затем...
-
ПРОСТРАНСТВА ЦЕННОСТЕЙ, Ценности и цели - Системная революция и принцип дуального управления
Ценности и цели Целесообразность существования систем проявляется на микро-, макро - и метауровнях и включает в себя два аспекта: Ценностный и Целевой ....
-
УРАВНЕНИЕ ПЛОСКОСТИ Любая Поверхность есть геометрическое место точек, ее составляющих, определенное уравнением Иными словами, все точки, которые...
-
Свойства ситуационных пространств - Системная революция и принцип дуального управления
Ситуационные пространства так же материальны, как и существующие в них объекты. В силу этого они оказывают определенное влияние на возникающие в них...
-
ПРОСТРАНСТВА ИНФОРМАЦИИ, Информация - Системная революция и принцип дуального управления
Информация Современное общество немыслимо без интенсивных информационных обменов, идущих на самых различных уровнях. Читаем ли мы газету или книгу,...
-
Пространства ситуаций - Системная революция и принцип дуального управления
Пространства ситуаций (или ситуационные пространства) задаются отношениями порядка на множествах структурных образований. И в этом смысле они аналогичны...
-
Пространство - логически мыслимая форма, служащая средой существования материальных объектов и процессов. Пространство характеризует структурность и...
-
ПРОСТРАНСТВА СИТУАЦИЙ, Сферы и образы - Системная революция и принцип дуального управления
Сферы и образы Сущность любой реальной системы проявляется в процессах обменных взаимодействий. В зависимости от уровня развития и характера системы...
-
Программное обеспечение контроллера (ПО) физически расположено в микросхеме типа К573РФ4 объемом 8 Кбайт. При работе используется ОЗУ К537РУ10 2 Кбайта....
-
Матрицей называется прямоугольная таблица чисел, содержащая m строк одинаковой длины. Матрицы равны между собой, если равны все их соответствующие...
-
Элементы матричного анализа - Методы решения системы линейных уравнений
Вектором, как на плоскости, так и в пространстве, называется направленный Отрезок , то есть такой Отрезок , один из концов которого выделен и называется...
-
Векторы, и образуют правую тройку векторов. - Сферический треугольник и его применение
Свойства: 1. 2. 3. 4. 13. Смешанное произведение векторов и его свойства . Смысл смешенного произведения: сначала два вектора векторно перемножают, а...
-
СКАЛЯРНОЕ ПРОИЗВЕДЕНИЕ ВЕКТОРОВ Скалярным произведением двух векторов иназывается число S =|| || сos (). Эта операция обозначается. В частности,...
-
Евклидовы кольца - Евклидовость в математике
Кольцо целостности Е называется евклидовым, если на множестве Е можно определить функцию е, значение которой является целыми неотрицательными числами,...
-
Пусть на некотором отрезке [a, b] задана кусочно-монотонная функция f(x). Покажем, что данную функцию в точках ее непрерывности можно представить в виде...
-
Теорема 1. Предел постоянной равен самой постоянной. . Доказательство. f(x)=с, докажем, что . Возьмем произвольное e>0. В качестве d можно взять любое...
-
Определители (детерминанты) - Методы решения системы линейных уравнений
Определение. Определителем квадратной матрицы А= называется число, которое может быть вычислено по элементам матрицы по формуле: Det A = , где (1) М1к -...
-
Конечные прямые и подпрямые произведения - Формационные основы универсальных алгебр
На протяжении всего параграфа будут рассматриваться только конечные проиведения. Пусть алгебра и - подалгебра алгебры. Тогда отображение Такое, что для...
-
Ряды конгруэнций - Формационные основы универсальных алгебр
5.1. Конечная цепь конгруэнции алгебры А вида (1) , Называется Рядом конгруэнций, а число -- Длиной ряда. Фактор алгебры называется Главным , если и из ,...
-
Матрицы над евклидовым кольцом - Евклидовость в математике
Введем следующее определение: строку над евклидовым кольцом Е будем называть канонической, если, кроме главного элемента, все остальные ее элементы...
-
Симплекс - метод - Интегральное и дифференциальное исчисление
Другой способ решения задач линейного программирования - симплекс-метод. Он, в отличие от геометрического, является полностью аналитическим, что...
-
Актуальность исследования Цель исследования: Изучение теоретических и практических аспектов евклидовости в математике Задачи исследования: 1. Изучить...
-
В 1930 году Дж. Биркгофом и Дж. фон Нейманом была сформулирована и доказана одна из основных эргодических теорем - теорема о предельных вероятностях:...
-
Линейные уравнения и системы линейных уравнений над кольцом целостности - Евклидовость в математике
Математическое предположение, которое может быть только истинным, или ложным, "существует столбец значений неизвестных такой, что соответствующие этому...
-
В школьной алгебре одночленом от некоторой буквы x называется алгебраическое выражение вида, где a - некоторое число, x - буква, m - целое...
-
Методы вычисления определителей
Вычислить сумму матриц kA+mB, если, Вычисление линейный уравнение Вычислить определитель третьего порядка: Решить систему линейных уравнений методом...
-
Определение . Алгебраическим дополнением минора матрицы называется его Дополнительный минор , умноженный на (-1) в степени, равной сумме номеров строк и...
-
Сравнение множеств Определение. Множества A и B называются равномощными, если между A и B существует взаимно однозначное соответствие. Утверждение....
-
Известно оптимальное решение X*=(0;0;1;1) задачи линейного программирования: Составьте двойственную задачу и найдите ее оптимальное решение по теореме...
-
Свойства операции умножения матриц - Методы решения системы линейных уравнений
1)Умножение матриц не коммутативно, т. е. АВ ВА даже если определены оба произведения. Однако, если для каких - либо матриц соотношение АВ=ВА...
-
Обозначения: Длина вектора, модуль (абсолютная величина): Сумма векторов: (правило треугольника) (рис. 1.22); (правило параллелограмма) (рис. 1.23);...
-
Гомоморфизм алгебр. Конгруэнции - Формационные основы универсальных алгебр
3.1. Отображение f из алгебры A в алгебру B называется гомоморфизмом, если для любых элементов и любой n-арной операции справедливо равенство Если же...
-
ПРАВАЯ И ЛЕВАЯ ТРОЙКИ ВЕКТОРОВ Линейно независимые векторы, и образуют Правую Тройку векторов, если они имеют такую же ориентацию, как соответственно...
-
ОПРЕДЕЛЕННЫЕ ИНТЕГРАЛЫ, Интегральные суммы - Определенные интегралы
Интегральные суммы Пусть функция задана на сегменте, . Обозначим символом разбиение сегмента при помощи некоторых несовпадающих друг с другом точек на...
-
Пусть { , , ..., } - множество возможных состояний некоторой физической системы. В любой момент времени система может находиться только в одном...
-
О квази-клике. - Использование квази-клик для анализа графа рынка России
Квази-клика - представляет собой релаксацию строгого условия полноты клики, то есть допускается отсутствие некоторых ребер в искомом подграфе. На данный...
-
Завод по изготовлению телевизоров, находясь в состоянии 1, может увеличить спрос путем организации рекламы. Это требует добавочных затрат и уменьшает...
-
Определения - Экономико-математическая детерминированная модель
Никакое определение не может в полном объеме охватить реально существующую деятельность по математическому моделированию. Несмотря на это, определения...
-
Некоторые векторные равенства Среди векторных соотношений можно выделить несколько важных соотношений, называемых здесь основными. Эти основные...
-
Площадь криволинейной трапеции - Определенный интеграл
Определение . Фигура, ограниченная графиком непрерывной, знакопостоянной функции f(x), осью абсцисс и прямыми X=a, x=b, Называется криволинейной...
Евклидово пространство