Деякі застосування потрійних інтегралів - Застосування подвійного і потрійного інтегралів
Задачі механіки. Нехай речовину неперервно розподілено в тривимірній області G з густиною (x, y,z) = (N). Розділемо G на елементарні частини. Маса відповідної елементарної частини дорівнює dm = dV, де dV = dxdydz - елемент об'єму в декартовій системі координат. Елементарні статичні моменти відносно координатних площин визначаються рівностями dM = zdm ; dMyz = xdm ; dM = ydm. Після граничного переходу маса і статичні моменти тіла, якому відповідає область G, визначаються відповідними формулами:
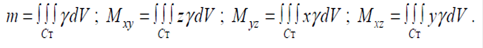
(3.5)
Координати центра маси (xc, yc, zc) тіла задовольняють співвідношення
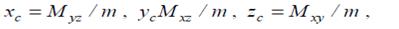
(3.6)
Згідно з визначенням цього поняття.
Елементарні моменти інерції відносно координатних осей дорівнюють:
Dlx = (у2 + z2 )dm; dlv = (х2 + z2 )dm ; dlz =(x2 + у2 )dm,
Де у+z, x+z, x+y - квадрати віддалей точки N(x, y, z) від відповідної вісі Ох, Оу, Oz. Згідно з визначенням, моментом інерції системи точок відносно осі називають суму добутків мас цих точок на квадрати їх віддалі до осі. Отже, моменти інерції всього тіла дорівнюють:
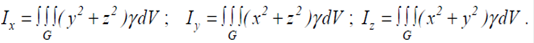
(3.7)
Момент інерції тіла відносно початку координат:
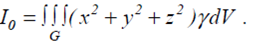
(3.8)
Приклад. Знайти центр маси однорідного тіла, обмеженого параболоїдом 2z = х2 + у2 і кулею х2 + у2 + z = 3 .
Розв'язання. Маємо тіло обертання навколо осі Oz (рис. 3.4). Тіло однорідне, тому візьмемо (x, y,z) = 1. Оскільки вісь Oz є віссю симетрії тіла, то хс = ус. = 0. Отже, шуканою є величина zc
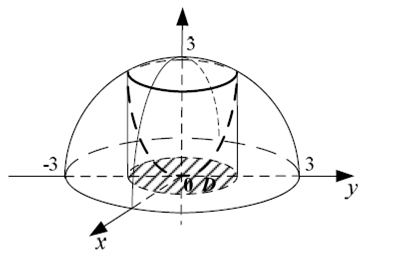
Рис. 3.4
Але спочатку знайдемо проекцію лінію перетину даних поверхонь з системи:

Формулою (3.5) маємо:
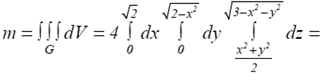
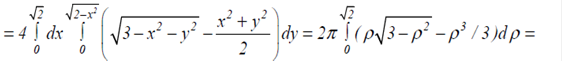
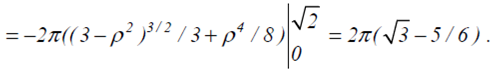
У повторному інтегралі перейшли до полярної системи координат:
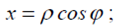
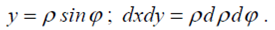
За формулою (3.6) обчислимо аналогічно статичний момент:

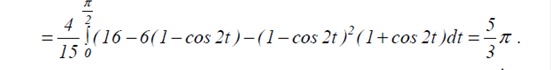
За формулою (3.6) обчислюємо:
Похожие статьи
-
Застосування подвійного інтегралу до задач механіки Статичні моменти. Центр маси пластини. Нехай матеріальна пластина в площині Оху має форму області D;...
-
Застосування потрійних інтегралів до задач геометрії та механіки - Вища математика
1. Потрійний інтеграл в сферичній системі координат. Сферичними координатами точки називаються числа. Де - кут між віссю і радіус-вектором точки ; -...
-
Площа плоскої області обчислюється за формулою (6) У полярній системі координат формула (6) має вигляд (7) Об'єм циліндричного тіла, обмеженою зверху...
-
Заміна змінних у подвійному інтегралі - Застосування подвійного і потрійного інтегралів
Нехай функція f(x, у) неперервна в деякій замкненій і обмеженій області D і існує інтеграл: I=. Припустимо, що за допомогою формул Х = x(u, v), у = у(и,...
-
Заміна змінних у потрійному інтегралі - Застосування подвійного і потрійного інтегралів
Нехай обмежена, правильна, замкнена область G простору (х, y, z) взаємно однозначно відображається на область G* простору (u, v,w) за допомогою...
-
Подвійний інтеграл Зміна порядку інтегрування в подвійному інтегралі Хай маємо область D як показано на рис. 1: Рис. 1 І вона задається нерівностями:...
-
Обчислення потрійного інтегралу Нехай область G розташована у тривимірній прямокутній системі координат. Вона обмежена знизу і зверху поверхнями z = (x,...
-
Обчислення подвійного інтегралу - Застосування подвійного і потрійного інтегралів
Обчислення подвійного інтегралу. Обчислення подвійного інтегралу за формулою (1.2) як границі інтегральної суми, так само як і у випадку визначеного...
-
Робота сили Якщо - сила, яка вздовж кривої L змінюється по величині та напрямку, то при переміщенні матеріальної точки одиничної маси під дією цієї сили...
-
Висновок, Список використаної літератури - Застосування подвійного і потрійного інтегралів
У даній роботі ми спробували найбільш широко розкрити застосування кратного інтегралу. Завдяки кратним інтегралам ми можемо обчислювати площу плоскої...
-
Кратні інтеграли - розділ математичного аналізу. До поняття кратних інтегралів привели задачі про знаходження об'єму циліндричного тіла, про обчислення...
-
У випадку криволінійного інтегралу функція інтегрується по кривій. Аналогічно для тривимірного простору: Обчислення криволінійного інтегралу І-го роду...
-
Застосування визначених інтегралів, Обчислення площ - Визначений інтеграл
Обчислення площ Якщо на відрізку [а, b] функція F (х)0 , то згідно з форму-лою (4), обчислення площі криволінійної трапеції, зображеної на малюнку 1,...
-
Обчислення потрійних інтегралів в декартових і циліфндричних кординатах - Вища математика
1. Поняття потрійного інтеграла Розглянемо в просторі деяку замкнену область. Нехай в області і на її границі визначена деяка неперервна функія, де -...
-
Обчислення подвійних інтегралів в полярній системі координат - Вища математика
Відомо, що полярні координати довільної точки зв'язані з її декартовими координатами формулами (1) Де Поняття подвійного інтеграла в полярній системі...
-
Визначення : Алгебраїчні лінійні рівняння називаються однорідними, якщо в них вільний член дорівнює нулю. Розглянемо таку систему, що має вигляд: (10.1)...
-
Застосування парної лінійної регресії до прогнозування економічних показників Прогноз - це ймовірностне, науково обгрунтоване судження щодо перспектив,...
-
Визначення : Скалярний добуток двох векторів і дорівнює добутку модулів цих векторів на косинус кута між ними . (6.1) Таким чином, скалярний добуток двох...
-
У роботі розглядаються безперервні функції F З періодом 2p і їх наближення тригонометричними поліномами. Через Tn(x) Позначається тригонометричний...
-
З математичної точки зору розв'язки (1) і (2) мають однаковий зміст. О-1 Подвійним інтегралом від функції по області називається границя (3) За умови, що...
-
Натрій в природі, Отримання, застосування натрію - Натрій: історія, властивості
У природі лужні елементи трапляються лише у вигляді солей. Найважливішими мінералами Натрію є кам'яна сіль або галіт NaCl, чилійська селітра NaNO3,...
-
Застосування парної лінійної регресії в економічних дослідженнях Зв'язок між різними явищами в економіці складний і різноманітний. На рівень розвитку...
-
Переробка платиновміщуючих шламів - Виробництво і застосування платини
При електролітичному рафінуванні міді і нікелю платинові метали концентруються в анодних шламах, де їх зміст залежно від складу початкових руд...
-
Застосування економіко-математичних методів для оптимізації бюджетних видатків на охорону здоров'я
Застосування економіко-математичних методів для оптимізації бюджетних видатків на охорону здоров'я Постановка проблеми. Сучасний стан фінансування...
-
ЗАТ "Біола" випускає три види продукції: напій на основі сиропу з цукром, напій на основі сиропу з цукрозамінником, сік. У поточному місяці прогнозуються...
-
ЙОД Сировиною для промислового одержання йоду служать нафтові бурові води, морські водорості, а також маткові розчини чилійської (натрієвої) селітри, що...
-
Фізичні властивості. - Виробництво і застосування платини
Платина дуже тугоплавкий метал, кристалізується в гранецентровані кубічні (р. ц. до.) грати. При дії на розчини солей відновниками метал може бути...
-
І. Визначення : Мішаним добутком трьох векторів і називається добуток виду, де два перших вектори перемножуються векторно, а їхній добуток множиться...
-
Нехай функція F (х) задана на відрізку [a, b] . Розіб'ємо цей відрізок на N частин точками ділення А = х0 < x1 < x2 < ... < хn = b У кожному...
-
Деякі відомості про нейронні елементи - Нейроматематика
Теоретичні основи нейроматематики були закладені на початку 40-х років. У 1943 році У. Маккалох і його учень У. Пітс (U. MCCULOCH and W. PITTS)...
-
Моменты инерции сечения - Геометрические характеристики поперечных сечений
В дополнение к статическим моментам рассмотрим еще три следующих интеграла: Через Х и У обозначены текущие координаты элементарной площадки DF в...
-
Конструкція та принцип дії турбодетандерної установки Принцип роботи турбодетандера заснований на розширенні газу в робочому колесі. Газ віддає енергію,...
-
Дипольный момент молекулы и связи
Представим себе, что можно найти "центры тяжести" отрицательных и положительных частей молекулы. Тогда условно все вещества можно разбить на две группы....
-
Математична модель асинхронного двигуна (1.1)-(1.4) отримана для Т-подібної схеми заміщення, що показана на рис.1, в той час як приведені в завданні...
-
Цей параграф носить допоміжний характер. Тут встановлюється декілька простих властивостей модуля нерперывности вищих порядків. Всі функції F1 , що...
-
Інтегральне числення функції кількох змінних. - Вища математика
Розглянемо функцію двох змінних, областю визначення якої є деяка квадровна область. Зауважимо, що коли межа області складається із численного числа...
-
Знаходження границь та частинних похідних і диференціалів функцій двох змінних
Знаходження границь та частинних похідних і диференціалів функцій двох змінних Будь-який упорядкований набір з П Дійсних чисел Х 1 ,...,x N позначається...
-
Задача Коші - Лінійні різницеві рівняння зі сталими коефіцієнтами
Нехай - фундаментальна система, нормована при тобто , Де - одинична матриця. Загальний розв'язок однорідної системи має вигляд . Вважаючи невідомою...
-
Сферические координаты - Интегральное и дифференциальное исчисление
Пусть Где R - радиус-вектор точки М , т. е. R - расстояние от точки М до начала координат: Ц - угол между положительными направлением оси 0X и лучом (-...
-
Пусть сначала область интегрирования есть K-мерный пространственный параллелепипед (рис. 5), стороны которого параллельны осям координат. Каждый из...
Деякі застосування потрійних інтегралів - Застосування подвійного і потрійного інтегралів