Прості властивості модулів неперевності - Дослідження якнайкращих наближень безперервних періодичних функцій тригонометричними поліномами
Цей параграф носить допоміжний характер. Тут встановлюється декілька простих властивостей модуля нерперывности вищих порядків. Всі функції F1, що розглядаються тут, f2 ... - Безперервні.
ЛЕМА 1. Для будь-якого натурального До і будь-якого Dі0
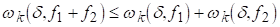
(2.1)
Доказ: за визначенням
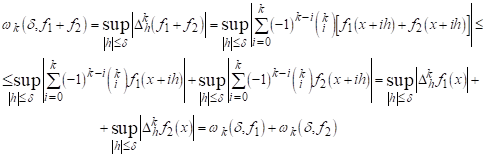
Лема доведена.
ЛЕМА 2. Хай F І L -натуральные числа, L<k. Тоді для будь-якого Dі0
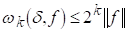
(2.2)
І (2.3)
Доказ: Покладемо
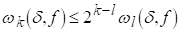
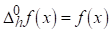
Тоді для 0Јl<k маємо
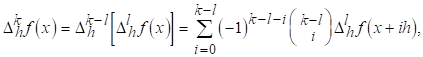
Звідки
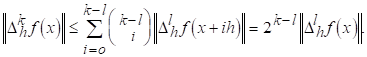
Звідси при L=0 витікає, що
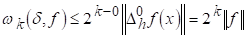
,
А при 0<l<k
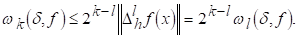
Вважаючи в (2.3) L=1, знаходимо, що
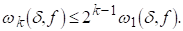
З цієї нерівності видно, що для будь-якого натурального До
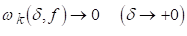
. (2.4)
ЛЕМА 3. Для будь-якого натурального До Модуль безперервності К-го порядку є безперервною функцією від D.
Доказ: Хай Маємо
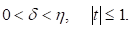
Звідси
І
Таким чином
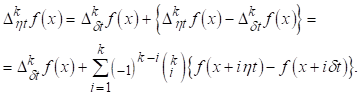
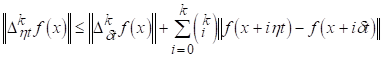
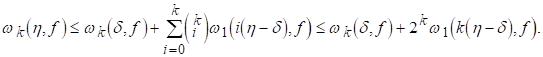
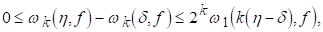
І так як при то звідси витікає безперервність функції і лема доведена.
ЛЕМА 4. Хай До І P-натуральные числа. Тоді для будь-якого Dі0
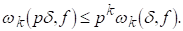
(2.5)
Доказ: Індукція по До Дає формулу
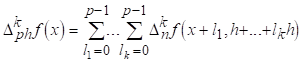
Звідси
І
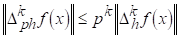
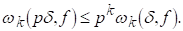
Лема доведена.
ЛЕМА 5. Хай К-натуральное число, D>0, H>0. Тоді
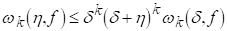
(2.6)
Якщо крім того 0<d<h, то
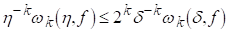
(2.7)
Доказ: Доведемо спершу нерівність (2.6). Розглянемо випадок для HЈd. Знайдемо натуральне число P З умов
(2.8)
Тоді H<pd-1, і так як - є неубутною функцією від H, то беручи до уваги (2.5) і (2.8), отримаємо
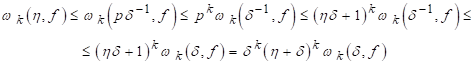
Розглянемо випадок для H<d. Знайдемо натуральне число P З умов
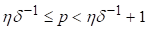
(2.9)
Тоді H<pd, і так як - є неубутною функцією від H, то беручи до уваги (2.5) і (2.9), отримаємо
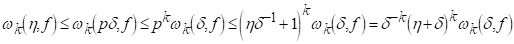
,
І нерівність (2.6) доведена. Нерівність (2.7) витікає з (2.6), оскільки D+hЈ2h для 0<d<h.
Нерівність (2.7) показує, що для будь-якої Fє0 і будь-якого натурального До
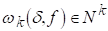
(2.10)
Лема доведена.
ЛЕМА 6. Хай F Має r-ю похідну F(r). Тоді
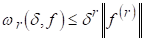
(2.11)
І для будь-якого натурального До
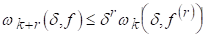
(2.12)
Доказ: Обидві нерівності безпосередньо витікають з формули
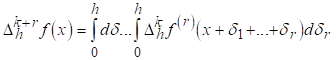
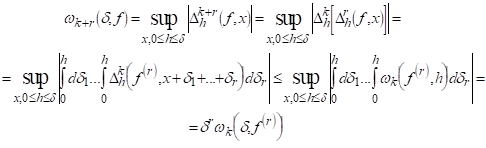
Якщо K=0, то ми отримуємо формулу (2.11). Лема доведена.
Похожие статьи
-
У цьому параграфі узагальнюються і уточнюються так звані "зворотні теореми" теорії наближення. Мова йде про оцінці диференціальних властивостей функції f...
-
Звернемося тепер до розгляду наступного питання: які необхідні і достатні умови того, щоб Де - задана незростаюча функція? Наскільки нам відомо, це...
-
У роботі розглядаються безперервні функції F З періодом 2p і їх наближення тригонометричними поліномами. Через Tn(x) Позначається тригонометричний...
-
Тут буде отримано невелике посилення теореми Джексона про якнайкращі наближення періодичних функцій тригонометричними поліномами. Лема 7. Хай дано...
-
У цьому параграфі встановлюється, що якщо тригонометричний поліном Tn(x) Близький до заданої функції F , то його модулі безперервності можна оцінити...
-
У цьому параграфі формулюється одне узагальнення нерівності С. Н. Бернштейна для похідних від тригонометричного полінома. Теорема 2. Хай. Тоді для...
-
Дипломна робота присвячена дослідженню якнайкращих наближень безперервних періодичних функцій тригонометричними поліномами. У ній даються необхідні і...
-
Приклад 1. Хай Тоді при кожному Приклад 2. Хай графік функції F(x) Має вигляд, зображений на рис.8.1. Тоді графік функції показаний на рис.8.2. Мал. 8.1....
-
Знаходження границь та частинних похідних і диференціалів функцій двох змінних
Знаходження границь та частинних похідних і диференціалів функцій двох змінних Будь-який упорядкований набір з П Дійсних чисел Х 1 ,...,x N позначається...
-
Загальні властивості функцій - Функції та способи їх задання
Означення : Множина всіх значень аргумента, для яких можна обчислити значення функції, називається природною областю визначення функції. Область...
-
Визначення : Скалярний добуток двох векторів і дорівнює добутку модулів цих векторів на косинус кута між ними . (6.1) Таким чином, скалярний добуток двох...
-
Теорема 1. Нехай послідовності (хП) і (уП) мають відповідно границі а і b. Тоді послідовність (xN+yN) має границю а + b. Теорема 2. Нехай послідовності...
-
Положення підприємства багато в чому визначається його фінансовим станом, у зв'язку з чим аналізові фінансових результатів діяльності надається велике...
-
ДИФЕРЕНЦІАЛЬНЕ ЧИСЛЕННЯ ФУНКЦІЇ ОДНІЄЇ ЗМІННОЇ, Поняття межі послідовності - Основи вищої математики
Математика алгебра геометрія тригонометрія Поняття межі послідовності Визначення : Нехай кожному натуральному числу n=1, 2, 3, ... за деяким законом...
-
Межа функції - Основи вищої математики
Розглянемо деякі випадки зміни функції або прагнення аргументу Х до деякої межі " А " або до. Визначення 1: Нехай функція y=f(х) визначена в деякій...
-
Функцією у = f(x) називається така відповідність між множинами D і Е, при якій кожному значенню змінної х відповідає одне й тільки одне значення змінної...
-
Уже из приведенного примера видно, что "управлять" величинами изменения значимости тех или иных элементов иерархии достаточно проблематично вследствие ее...
-
Теорема 1. Похідна від функції logax дорівнює, тобто якщо y=logax, то . (11.1) Теорема 2. Похідна від sinx є cosx, тобто якщо y=sinx, то Y =cosx. (11.2)...
-
Нехай функція F (х) задана на відрізку [a, b] . Розіб'ємо цей відрізок на N частин точками ділення А = х0 < x1 < x2 < ... < хn = b У кожному...
-
Задачі, що привели до поняття визначеного інтеграла Розглянемо дві задачі -- геометричну та фізичну. 1. Обчислення площі криволінійної трапеції . Нехай...
-
Визначники та їх властивості - Основи вищої математики
До поняття визначника приходимо, розглядаючи системи алгебраїчних рівнянь першого степеня. Розглянемо систему рівнянь: (2.1) X та y -- невідомі,...
-
В даний час існує ряд критеріїв для оцінки піно-утворення: 1. Властивості одинарної плівки. Ще Плато встановлено, що час життя плівки обернено...
-
Расчет питания. Формула Шкарина. - Расчеты при приготовлении водных растворов
Vсут=800 50n Если n - число недель, недостающее до 8-ми недель, тогда формула берется со знаком минус. Если n - число месяцев больше 2-х, формула берется...
-
Визначення : Сукупність лінійно незалежних векторів, по яких відбувається розкладання інших векторів, називається Базисом . Отже, у площині можуть...
-
Теоретичні основи оптимізаційних рішень Умови оптимальності у формі принципу максимуму дають, узагалі говорячи, достатню інформацію для рішення задачі...
-
Інтегрування частинами, Заміна змінної у визначеному інтегралі - Визначений інтеграл
Якщо проінтегрувати обидві частини рівності D[u(x) - v(x)] = v(x)du(x) + u(x)dv(x) В межах від А до B , то одержимо Звідси одержуємо важливу формулу...
-
Зв'язок між визначеним та невизначеним інтегралами Означення 2. Визначений інтеграл з постійною нижньою межею та змінною верхньою межею називають...
-
Подвійний інтеграл Зміна порядку інтегрування в подвійному інтегралі Хай маємо область D як показано на рис. 1: Рис. 1 І вона задається нерівностями:...
-
Розкриття невизначеностей. Формула Тейлора - Основи вищої математики
1. Невизначеність виду 0/0. Теорема 1 ( Правило Лопіталя - Гійом 1661-1704 р., французький математик, автор першого друкованого підручника по...
-
Диференціал, Визначення диференціала. - Основи вищої математики
Визначення диференціала. Формули й правила диференціювання. Використання диференціала для наближених обчислень. Основні теореми диференціального...
-
Теорема Маркова - Невід'ємні матриці
Нехай для стохастичної матриці P існує натуральне число k0 таке, що (тобто всі елементи додатні). Тоді 1. (існування границі матриці означає, що існує...
-
Теореми про межі. Чудові межі - Основи вищої математики
Будемо розглядати сукупність функцій, які залежать від того самого аргументу Х , при цьому Ха або Х . Доведення проводиться для одного із цих випадків,...
-
Основна ідея розпаралелювання обчислень - мінімізація часу виконання задачі за рахунок розподілу навантаження між декількома обчислювальними пристроями....
-
Способы формирования выборочной совокупности - Основы эконометрики
Способ отбора Определяет конкретный механизм или процедуру выборки единиц из генеральной совокупности. В практике выборочных обследований наибольшее...
-
Метод Гауса - Основи вищої математики
( Карл Фрідріх Гаус (1777-1855) іноземний член Петербурзької АН (1824), німецький математик. Праці: вища алгебра, диференціальна геометрія, математична...
-
Системи лінійних алгебраїчних рівнянь - Основи вищої математики
1. Будемо розглядати систему з "m" лінійних алгебраїчних рівнянь із "n" невідомими (8.1) Рішенням такої системи називається такий набір чисел Х 1, Х 2,...
-
Обчислення потрійного інтегралу Нехай область G розташована у тривимірній прямокутній системі координат. Вона обмежена знизу і зверху поверхнями z = (x,...
-
Символічно позначається. Границя числової посл. Число а-границя числ. посл. xN, якщо {xN-a}-н. м. >0N:nN:{xN-a}< A-<xN<a+ Послідовності, що...
-
Следствия теоремы, Послесловие к доказательству - Об одной теореме теории чисел
Не существует ЦЕЛЫХ чисел, для которых выполняется равенство (1). При четных значениях показателя степени уравнение вида (1) идентично как для...
-
Логарифм числа b по основанию a (logAB) определяется как показатель степени, в которую надо возвести число a, чтобы получить число b (Логарифм существует...
Прості властивості модулів неперевності - Дослідження якнайкращих наближень безперервних періодичних функцій тригонометричними поліномами