Численные методы. Интерполяция Ньютона


Задание 1

Запишите порядок выполняемых вами операций, оцените погрешности их результатов, вычислите и запишите искомое значение. Определите число верных знаков.

Решение

Для вычисления искомого значения необходимо определить порядок действий, а также для результата каждого действия определить абсолютную и относительную погрешности, а также число верных знаков результата.

Вычисления приведены в таблице 1.

Функция гаусс уравнение итерация

Таблица 1 - Порядок действий и результаты вычислений

Порядок действий

Выражение

Результат

Абсолютная погрешность

Относительная погрешность

Число верных знаков

*

A

0,245600

0,000500

0,002036

3

*

B

0,200780

0,000030

0,000149

4

*

C

0,008000

0,000130

0,016250

1

1

A + b

0,446380

0,000530

0,001187

3

2

(a + b) * с

0,003571

0,000062

0,017437

2

3

A - b

0,044820

0,000530

0,011825

2

4

(a + b) * c / (a - b)

0,079675

0,002331

0,029262

1

5

[ (a + b) * c / (a - b) ]^ 2

0,006348

0,000372

0,058525

1

6

1 + c

1,008000

0,000130

0,000129

4

7

Ln (1 + c)

0,007968

0,000129

0,016185

1

8

[(a+b)*c/(a-b)]^2*ln(1+c)

0,000051

0,000004

0,074710

1

После вышеперечисленных действий было получено искомое значение, равное числу "0,000051" при количестве верных знаков "1"

Ответ: Искомое значение: 0,000051.

Число верных знаков: 1.

Задание 2

Выяснить погрешность задания исходных данных,

Выясните погрешность задания исходных данных, необходимую для получения результата с m верными значащими цифрами.

Решение.

Имеем функцию нескольких переменных. Исходя из принципа равных влияний и формулы оценки абсолютной погрешности дифференцируемой функции нескольких переменных имеем формулу требуемой абсолютной погрешности переменных

.

Выполним вычисления и запишем их в таблицу 2.

Таблица 2 - Вычисление дифференцируемой функции нескольких переменных

Условие

A

0,245600

B

0,200780

C

0,008000

Вспомо-гательные переменные

A + b

0,446380

A - b

0,044820

C + 1

1,008

Ln(c+1)

0,00796817

U

(a+b)*c/(a-b)^2*ln(1+c)

0,000051

Du / da

C^2*(2*a + 2*b)*ln(c + 1)/(a - b)^2 - 2*c^2*(a + b)^2*ln(c + 1)/(a - b)^3

0,0020305

Du / db

C^2*(2*a + 2*b)*ln(c + 1)/(a - b)^2 + 2*c^2*(a + b)^2*ln(c + 1)/(a - b)^3

0,002483797

Du / dc

C^2*(a + b)^2/((a - b)^2*(c + 1)) + 2*c*(a + b)^2*ln(c + 1)/(a - b)^2

0,018943488

Ответ

ДU

0,00005

Дa

0,000000034

Дb

0,0000000414

Дc

0,0000003157

Ответ: требуемые абсолютные погрешности переменных:

Дa = 0,000000034; Дb = 0,0000000414; Дc = 0,0000003157.

Задание 3

Решить СЛАУ методом Гаусса и с точностью до е=0.001 методом простой итерации:

Решение:

Метод Гаусса (метод исключения неизвестных)

Представляет собой метод решения линейной системы (состоящий из уравнения и неизвестных) путем преобразования расширенной матрицы к треугольной форме.

На первом этапе нужно зафиксировать расширенную матрицу системы (составленную из коэффициентов):

Матрицы можно преобразовывать путем манипуляций со строками матрицы (умножение, сложение и т. д.)

Шаг 1. Умножение строки "1" на (-0,5).

[для сложения со строкой "3" (строка 1 остается неизменной)]

Шаг 2. Умножение строки "2" на (0,1).

[для сложения со строкой "3" (строка 2 остается неизменной)]

Получена оптимальная расширенная матрица системы:

Шаг 3. Из уравнения системы №3 выразим переменную x3:

3,2x3 = 3,2 ;x3 = 1.

Шаг4 . Из уравнения системы №2 выразим переменную x2:

5x2 - 2x3 = 7;5x2 = 7 - 2;x2 = 1.

Шаг4 . Из уравнения системы №1 выразим переменную x1:

2x1 - x2 = 3;2x1 = 4;x1 = 2.

Ответ: X1 = 2, x2 = 1, x3 = 1.

Общее решение:

Метод простой итерации (с точностью до е=0.001)

Представляет собой метод решения линейной системы за счет одношагового итерационного процесса (процесса последовательных приближений)

Прежде чем применять метод, необходимо переставить строки исходной системы таким образом, чтобы на диагонали стояли наибольшие по модулю коэффициенты матрицы.

Исходная матрица А уже является диагональной:

Приведем к виду (выразим х1, х2, х3):

Х1 = 1,5 + 0,5x2 ;

Х2 = 1,4 - 0,4x3 ;

Х3 = 1,333 - 0,333x1 + 0,333x2.

До произведения расчетов необходимо убедиться в выполнении условий сходимости полученной системы (Матрица B):

?B?1 = 0,666 < 1, ?B?2 = 0,833 < 1,

Что означает, что процесс итерации сходится к точному решению системы. Можем производить расчеты.

Расчеты сведены в таблицу были произведены в MS Excel (таблица 3)

Таблица 3 - Пошаговые итерации до получения погрешности е (max) < 10-І

N

0

1

2

3

4

5

6

7

8

9

10

X1

1,5

2,2

1,9

1,9

2

2

2

2

2

2

2

X2

1,4

0,867

0,88

1,044

1,007

0,986

1,002

1,002

0,999

1

1

X3

1,333

1,3

0,889

0,982

1,035

0,995

0,994

1,003

1

0,999

1

Е(max)

0,7

0,4107

0,1643

0,0821

0,0398

0,0159

0,0088

0,0035

0,0018

0,0009

X1 = 1,5 + 0,5X2Е(max) < 10-І

X2 = 1,4 - 0,4X3

X3 = 1,333 - 0,333X1 + 0,333X2

Ответ: X1 = 2, x2 = 1, x3 = 1

Задание 4

Методом простых итераций и Ньютона найти корни уравнения с точностью е=0.001

F(x): X3 + 2x - 7 = 0.

Решение:

Задача нахождения корня уравнения F(X) = 0 итерационным методом состоит из двух этапов:

    1. Отделение корней - отыскание приближенного значения корня или содержащего его отрезка; 2. Уточнение приближенных корней - доведение их до заданной степени точности

Приближенные значения корней (Начальные приближения) могут быть известны из физического смысла задачи, из решения аналогичной задачи при других исходных данных, или могут быть найдены графическим способом.

Действительные корни уравнения - это точки пересечения графика функции F(X) с осью абсцисс, достаточно построить график функции F(X) и отметить точки пересечения F(X) с осью Ох, или отметить на оси Ох отрезки, содержащие по одному корню.

Условия функции F(X) = 0:

    1. Функция F(X) непрерывна на отрезке [A, b] вместе со своими производными 1-го и 2-го порядка. 2. Значения F(X) на концах отрезка имеют разные знаки (F(A) * F(B) < 0). 3. Первая и вторая производные F' (X) и F'' (X) сохраняют определенный знак на всем отрезке.

Корень на отрезке [A, b] существует (один или несколько), исходя из условий 1), 2).

Обе функции правой и левой части монотонны, что говорит об единственном корне уравнения (условие 3)

Представим уравнение X3 + 2x - 7 = 0 в виде: X =0,5 (7 - x3);

Шаг 1. Отделим корни, построив графики двух полученных функций:

(1) y1 = x, и (2) y2= 0,5 (7 - x3) .

Графики функций будем строить для значений аргумента (X) на интервале: X ? (1, 2), так как при использовании в функции крайних элементов, функция F(x): x3 + 2x - 7 = 0 меняет знак.

Значения аргумента и функций на данном отрезке произведем в MS Excel (таблица 4)

На основе вычислений построим графики функций (рисунок 1)

Таблица 4 - Значения функций X = (7 - x3)/2 При x ? (1, 2)

X

1,00

1,10

1,20

1,30

1,40

1,50

1,60

1,70

1,80

1,90

2,00

Y? = x

1,00

1,10

1,20

1,30

1,40

1,50

1,60

1,70

1,80

1,90

2,00

Y? = (7-xі)/2

3,000

2,835

2,636

2,402

2,128

1,813

1,452

1,044

0,584

0,071

-0,500

F(x) = xі+2x-7

-4

-3,469

-2,872

-2,203

-1,456

-0,625

0,296

1,313

2,432

3,659

5

F'(x) = 3xІ+2

5

5,63

6,32

7,07

7,88

8,75

9,68

10,67

11,72

12,83

14

F''(x) = 6x

6

6,6

7,2

7,8

8,4

9

9,6

10,2

10,8

11,4

12
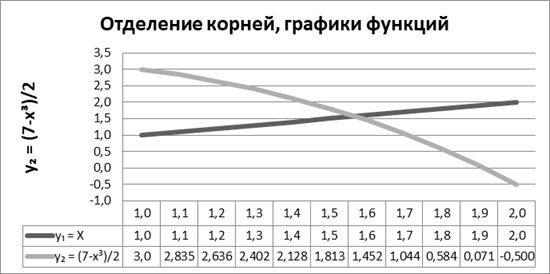
отделение корней, графики функций. интервал x &;#63; (1;2)

Рисунок 1. Отделение корней, графики функций. Интервал x ? (1;2)

Шаг 2. Сужение интервала приближенных корней уравнения.

Анализируя рисунок 1. можно утверждать, что решение уравнения лежит на интервале x ? (1,5; 1,6),

Графики функций будем строить для значений аргумента (x) на интервале: x ? (1,5;1,6)

Значения аргумента и функций на данном отрезке произведем в MS Excel (таблица 5)

На основе вычислений построим графики функций (рисунок 2)

Таблица 5 - Значения функций X = 0,5(7 - x3) При x ? (1,5; 1,6)

X

1,50

1,51

1,52

1,53

1,54

1,55

1,56

1,57

1,58

1,59

1,60

Y? = x

1,50

1,51

1,52

1,53

1,54

1,55

1,56

1,57

1,58

1,59

1,60

Y? = (7-xі)/2

1,813

1,779

1,744

1,709

1,674

1,638

1,602

1,565

1,528

1,490

1,452
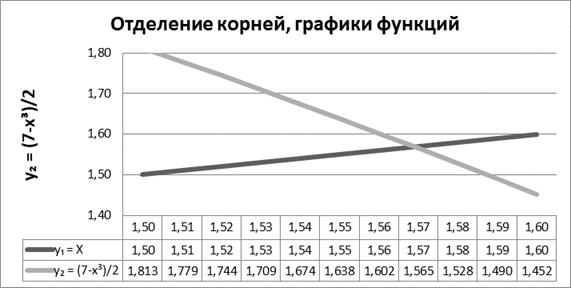
отделение корней, графики функций. интервал x &;#63; (1,5;1,6)

Рисунок 2. Отделение корней, графики функций. Интервал x ? (1,5;1,6)

Исходя из нового графика, мы видим, что отрезком, содержащий корень, является отрезок [1,55;1,6]

Шаг 3. Доведение приближенных корней до заданной степени точности.

Метод простой итерации (с точностью до е = 0.001)

Корень уравнения принадлежит отрезку [1,55 ; 1,6]. Используем уравнение, преобразованное раннее к виду: X = f(x)

F(x) = 0,5(7 - x3) ;

Функция F(x) не удовлетворяет условию сходимости, так как |F'(x)|> 1, где х - крайние точки

F'(x) = -1,5 x2F'(1,55) = -3,603 ;F'(1,6) = -3,84

Исходя из произведенных манипуляций, прибегаем к другому преобразованию: x3 = 7 - 2x; x = (7 - 2x)?

F(x) = (7 - 2x)?;

Функция F(x) удовлетворяет условию сходимости, |F'(x)|> 1.

F'(x) = 0,33(7 - 2x) Ї? F'(1,55) = -0,9162; F'(1,6) = -0,9242 (расчеты произведены в MS Excel)

Зададим начальное приближение x(0) = 1,55 и произведем вычисления на основе рекуррентного соотношения X(p+1)= (7 - 2x(p? С точностью до е=0.001 (таблица 6)

Таблица 6 - Метод простой итерации

P

0

1

2

3

X

1,550

1,574

1,568

1,569

(7-2x)?

1,5741

1,5676

1,5693

1,5688

X(p)-x(p-1)

-0,0065

0,0018

-0,0005

Е(max)<10-І

При 3-й итерации мы получили решение X = 1,569, удовлетворяющее заданным условиям точности.

Метод Ньютона (с точностью до е=0.001)

Для использования метода Ньютона необходимо, чтобы выполнялись условия сходимости функции F(x)= x3 + 2x - 7 :

    1) Функция дважды дифференцируема на отрезке [1,55 ; 1,6] (см. таблицу 2) 2) Отрезку [1 , 2] принадлежит только один простой корень; F(1,55) * f(1,6) < 0 == (- 0,176 * 0,296) < 0 ; 3) Производные F'(x) И F''(x) Сохраняют свой знак на отрезке [1,55 ; 1,6] (см. таблицу 2) 4) Начальное приближение x(0) (в данном случае x(0)=1,57) удовлетворяет неравенству: F(1,57), f''(1,57) > 0

Можем производить расчеты по формуле (расчеты произведем в MS Excel). Результаты в таблице 5.

Таблица 5 - Метод Ньютона (е=0.001)

P

0

1

2

X

1,57

1,568947

1,568946

F(x)

0,0099

0,0000

0,0000

F'(x)

9,3947

9,3848

9,3848

?x (е)

-0,0099

-0,00001

На 2-м шаге мы получили решение X = 1,569, удовлетворяющее заданным условиям точности.

Ответ: X = 1,569

Задание 5

Выписать интерполяционный многочлен Ньютона для узловых значений (xI,yI), заданных функцией Y=arcsin(x). Найти погрешность в точке X*= 0,1; xI= -0,5; -0,4; -0,3; -0,1; 0; 0,2.

Решение:

Интерполяционный полином в форме Ньютона PN(x) определяется при построении в виде:

Исходя из условия интерполяции для коэффициентов CI ,получим систему уравнений треугольного вида, из которой можно легко вывести коэффициенты C(0..n):

И т. д.

Коэффициенты приравниваются к Разделенным разностям (здесь - нулевого, первого и второго порядков).

Шаг 1. Вычислить значения функции Y = Arcsin(x) В известных узловых значениях X

Шаг 2. Вычислить раздельные разности, определить коэффициенты CI интерполяционного многочлена Ньютона.

Результаты шагов №1, №2 занесем в таблицу 6.

Таблица 6 - Интерполяционный метод Ньютона

I

0

1

2

3

4

5

X

-0,5

-0,4

-0,3

-0,1

0

0,2

F(x)=arcsin(x)

-0,5236

-0,4115

-0,3047

-0,1002

0,0000

0,2014

F0

-0,5236

-0,4115

-0,3047

-0,1002

0,0000

0,2014

F0,1

1,1208

1,0682

1,0226

1,0017

1,0068

F0,1,2

-0,2629

-0,1521

-0,0698

0,0171

F0,1,2,3

0,2771

0,2055

0,1738

F0,1,2,3,4

-0,1431

-0,0529

F0,1,2,3,4,5

0,1288

*Коэффициенты С0...j

Шаг 3. Записать интерполяционный многочлен Ньютона

PN(x) = -0,5236[CO]

+ 1,1208(x+0,5) - 0,2629(x+0,5)(x+0,4)[C1, C2]

+ 0,2771(x+0,5)(x+0,4)(x+0,3) - 0,1431(x+0,5)(x+0,4)(x+0,3)(x+0,1)[C3, C4]

+ 0,1288(x+0,5)(x+0,4)(x+0,3)(x+0,1)(x)[C5]

Шаг 4. Вычислить значение интерполяционного многочлена в точке X* = 0,1 и y = arcsin(0,1).

PN(0,1) = 0,100151;y = arcsin(0,1) = 0,100167

Шаг 5. Вычислить абсолютную и относительную погрешность в точке X* = 0,1.

Абсолютная погрешность Д = | PN(0,1) - arcsin(0,1) |= | 0,100151 - 0,100167 |= 0,000015

Относительная погрешность = Д / PN = 0,000015 / 0,100151 = 0,02 %.

Ответ: Д =0,000015, относительная погрешность = 0,02 %

Задание 6

Построить график решения в Matlab.

Y'=-4y + sin(x),y(0)=2,xе[0,6]

Похожие статьи




Численные методы. Интерполяция Ньютона

Предыдущая | Следующая