Методы вычислений
Задание 1
Разработать программу, которая на отрезке [-1,1] по формуле функции f(x) строит интерполяционную таблицу размерности n +1 с неравномерным шагом так, чтобы узлы интерполяции совпадали с нулями полинома Чебышева Tn(x) степени n +1, и интерполяционный полином Лагранжа.
Для контроля распечатать интерполяционную таблицу и значения интерполяционного полинома в узлах сетки.
Вычислить и выдать на печать значение интерполяционного полинома и значение функции f(x) при х = 0,1.
Код программы
// Подключаемые библиотеки
#include <iostream>
#include <conio. h>
#include <stdio. h>
#include <math. h>
#include < windows. h>
// заданная функции
Float f (float x)
{
Return (exp(x) - 3*x + 1);
}
// значение построенного интерполяционного полинома в форме Лагранжа
Float g (float X, float *x, float n)
{
Double p, s=0;
For (int i=0; i<=n; i++)
{
P = 1;
For (int j=0; j<=n; j++)
{
If (i==j) continue;
P *= (X-x[j])/(x[i]-x[j]);
}
S += p*f(x[i]);
}
Return s;
}
// Построение по формуле функции f(x) интерполяционной таблицы размерности n+1(узлы интерполяции совпадают с нулями полинома Чебышева)
// Массив x - узлы интерполяции (нули полинома Чебышева),
// Массив y - значения функции f(x) в узлах сетки.
// Массив z - значения интерполяционного полинома
Void xyz (float n, float *x, float *y, float *z)
{
For (int i=0; i<=n; i++)
{
X[i] = - cos(3.14159*(2*i+1)/(2*(n+1)));
Y[i] = f(x[i]);
}
For (int i=0; i<=n; i++) z[i] = g(x[i],x, n);
Printf (" x y(x) g(x) ");
For (int i=0; i<=n; i++)
{
If (i==18) // при заполнении страницы ждем нажатия клавиши
{
Printf ("Для продолжения нажмите любую клавишу... ");
_getch ();
Printf (" x y(x) g(x) ");
}
Printf (" % .3f%12f%12f ", x[i], y[i], z[i]);
}
}
Void main (void)
{
Setlocale(LC_ALL, "Russian"); //Для ввода русских символов
Float n = 25, *x, *y, *z;
// динамически создаем массивы из n+1 элементов
X = new float[n+1];
Y = new float[n+1];
Z = new float[n+1];
Printf ("Интерполяционная таблица (n=25) ");
Xyz (n, x, y, z);
Printf (" Значение функции при x = 0.1: %f", f(0.1));
Printf (" Значение интерполяционного полинома при x =0.1:%f ",g(0.1, x, n));
// освобождаем память, выделенную под массивы
Delete x; delete y; delete z;
System("pause"); // Для ожидания прекращения работы
}
Результат работы программы
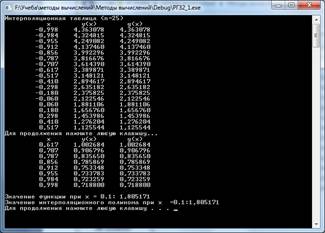
Рис. 1
Задание 2
Интеграл размерность полином чебышев
Построить алгоритм для вычисления приближенного значения интеграла по формуле Симпсона при n = 8 иn = 16, где n - это число интервалов, и оценки погрешности по правилу Рунге. Разработать программу, которая реализует этот алгоритм. На печать выдать два приближенных значения интеграла (при n = 8 и n = 16) и погрешность, найденную по правилу Рунге.
Код программы
//Подключаемые библиотеки
#include <conio. h>
#include <stdio. h>
#include <math. h>
#include <windows. h>
#include <iostream>
// Заданная функция
Float f1 (float x) {return 1/sqrt(2*x*x + 1.3);}
Void main(void)
{
Setlocale(LC_ALL, "Russian"); //Для ввода русских символов
/* a и b - границы отрезка
N - число отрезков
H - шаг
Q1 - значение интеграла при n=8
Q2 - значение интеграла при n=16
*/
Float a, b, h, Q1,Q2,Q; int n, i; // объявили переменные
Printf(" Численное интегрирование функций");
Puts(" *** Формула Симпсона ***");
A = 1; b = 2.8;
N = 8; h = (b-a)/n;
Q1 = f1(a)+f1(b);
Float s1=0, s2=0, x=a;
For (i=1; i<n; i++)
{
X += h;
If (i%2)
// сумма значений функции в точках с нечетными номерами
S1 += f1(x);
Else
// сумма значений функции в точках с четными номерами
S2 += f1(x);
}
Q1 = h/3*(Q1+4*s1+2*s2);
Printf (" n= 8:");
Printf (" Приближенное значение интеграла: %.7f", Q1);
N = 16;
H = (b-a)/n;
Q2 = f1(a)+f1(b);
S1=0; s2=0; x=a;
For ( i=1; i<n; i++)
{
X += h;
If (i%2)
// сумма значений функции в точках с нечетными номерами
S1 += f1(x);
Else
// сумма значений функции в точках с четными номерами
S2 += f1(x);
}
Q2 = h/3*(Q2+4*s1+2*s2);
Printf (" n= 16:");
Printf (" Приближенное значение интеграла: %.7f ", Q2);
Q= fabs(Q1-Q2)/15;
Printf(" Оценка погрешности по правилу Рунге: R=%.2e ",Q);
System("pause"); // Для ожидания прекращения работы
}
Результат работы программы
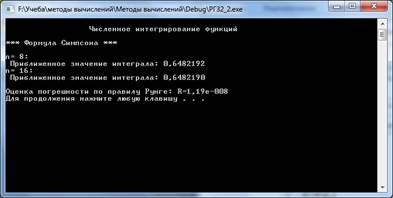
Рис. 2
Задание 3
Построить алгоритм для приближенного решения задачи Коши для обыкновенного дифференциального уравнения с начальным условием, на отрезке [0,1], с шагом h = 0.1 методом Рунге-Кутта четвертого порядка. Разработать программу, которая реализует этот алгоритм и выдает на печать таблицу приближенных и точных значений решения.
Код программы
//Подключаемые библиотеки
#include <conio. h>
#include <math. h>
#include <stdio. h>
#include <windows. h>
#include <iostream>
/* Глобальные переменные и массивы:
N - число узлов сетки
X[n] - массив узлов сетки
Y[n] - массив значений точного решения
U[n] - массив значений приближенного решения
H - шаг сетки
M, k - параметры, входящие в формулу точного решения
K1,K2,K3,K4 - коэффициенты метода Рунге-Кутта
*/
Const int n = 11;
Double x[n], y[n], u[n], h = 0.1,
M = 1.1, k = 2.5, K1, K2, K3, K4;
// возвращает значение функции (правой части ДУ)
Double f (double x, double y) { return - m*y+exp(k*x); }
Void main (void)
{
Setlocale(LC_ALL, "Russian"); //Для ввода русских символов
Printf("Численное решение задачи Коши для обыкновенных дифференциальных уравнений первого порядка");
// Метод Рунге-Кутта четвертого порядка
For(int i=0; i<n; i++)
{
Double a = i*h; x[i] = a;
// формула точного решения
Y[i] = (exp((k+m)*a)/(k+m)+1-1/(k+m))/exp(m*a);
}
U[0] = 1;
For(int i=0; i<n-1; i++)
{
K1=f(x[i], u[i]);
K2=f(x[i]+h/2, u[i]+h/2*K1);
K3=f(x[i]+h/2, u[i]+h/2*K2);
K4=f(x[i]+h, u[i]+h*K3);
// вычисление приближенного решения
U[i+1] = u[i]+h/6*(K1+2*K2+2*K3+K4);
}
// Вывод результатов на экран
Printf ("n Результаты расчета: ");
Printf (" Узлы сетки Точное решение Приближенное решение ");
For (int i=0; i<n; i++)
{
Printf (" %10.2f % -14.4f % -20.4f ", x[i], y[i], u[i]);
}
Printf(" ");
System("paus
Результат работы программы
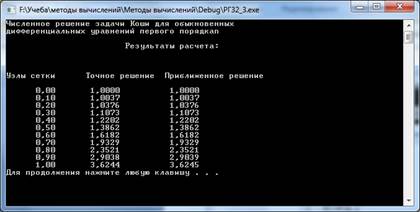
Рис. 3
Список использованных источников
- 1. Бахвалов Н. С. Численные методы / Н. С. Бахвалов, Н. П. Жидков, Г. М. Кобельков. - М.: Наука, 1987. - 600с. 2. Боглаев Ю. П. Вычислительная математика и программирование / Ю. П. Боглаев. - М.: Высшая школа, 1990.-544с. 3. Жидков Е. Н. Вычислительная математика / Е. Н. Жидков. - М.: Академия, 2010.- 208с.
Похожие статьи
-
Выведем в общем виде уравнение движения заданной динамической модели при помощи уравнений Лагранжа II рода. Полная кинетическая энергия: , Полная...
-
Вычисление интегралов, Вычисление сумм и произведений - Работа с символьным процессором
Система MathCAD содержит встроенную функцию для вычисления значений определенных интегралов приближенным численным методом. Ею целесообразно...
-
Интегрирование, Оператор интегрирования - Вычисление интегралов в Mathcad
Интегрирование в MathCAD реализовано в виде вычислительного оператора. Допускается вычислять интегралы от скалярных функций в пределах интегрирования,...
-
Вычислить приближенное значение определенного интеграла с подынтегральной функцией f(x) заданным методом и проверить точность вычислений по формуле...
-
Метод конечных элементов является численным методом для нахождения приближенных решений физических задач. В основе этого метода лежит разделение...
-
Многие организации, рассматривая вопрос о сетевой безопасности, не уделяют должного внимания методам борьбы с сетевыми атаками на втором уровне. В...
-
Разработка интерфейса, Разработка запросов - Высокоуровневые методы информатики и программирования
Программа, будет начинать работу с вывода главной формы, на которой будет располагаться самое главное меню, т. е. другими словами "панель навигации"....
-
Исходя из контекста решаемой задачи, для сравнительного анализа рассмотренных математических моделей обнаружения аномалий можно выбрать следующие...
-
Информационная система крупной организации, как правило, представляет собой исторически сложившуюся совокупность отдельно работающих систем, которые...
-
Среднее число исполнителей Чu, участвующих в разработке рассчитывается по формуле: Чu= , (10) Где Fд - полезный (действительный фонд времени одного...
-
Описание классов и методов - Обзор проблематики и теоретических основ электронного документооборота
В данной работе реализован один публичный класс Form1, в котором и происходит основной функционал программы, посредством выполнения методов по кнопкам....
-
Программная модель данных, получившая название "MapReduce", была создана несколько лет назад в компании Google, и там же была осуществлена первая...
-
Метод определения погрешности - Поверка и калибровка информационно измерительных систем
Метод определения погрешности аналоговых и цифро-аналоговых ИК для случая пренебрежимо малой случайной составляющей погрешности Если проверяемая точка...
-
Полученные результаты, Заключение, Литература - Вычисление максимума функции с некоторыми критериями
Заключение В данной курсовой работе была разработана программа, с помощью которой вычисляется максимум функции F(x) на отрезке [a, b]. В состав функции...
-
Поиск максимума функции F(x) на отрезке [a;b] - Вычисление максимума функции с некоторыми критериями
Постановка задачи: Необходимо численным методом найти максимум функции F(x)=-L(x1)x2+3.1L(x2)x+5 На отрезке [a;b] с точностью е, при том, что L(x1) и...
-
Вычислить максимум функции F(x)=-L(x1)x2+3.1L(x2)x+5 на отрезке [a;b] с точностью е. L(x1), L(x2) - значения интерполяционного многочлена, построенного...
-
Введение - Вычисление максимума функции с некоторыми критериями
Если функция, определенная и непрерывная в заданном промежутке, не является в нем монотонной, то найдутся такие части этого промежутка, в которых...
-
Теоретическая основа линейного программирования, Симплекс метод - Линейное программирование
Симплекс метод Симплекс метод - метод линейного программирования, который реализует рациональный перебор базисных допустимых решений, в виде конечного...
-
Технические требования Техническое задание данной работы требует разработать программу для визуального редактирования HTML-кода. Программа должна быть...
-
ИИС "Шлаковые расплавы" позволяет вести моделирование КЭ в нескольких "режимах", с полным набором получаемых свойств. 1. Моделирование комплекса свойств...
-
Шестой метод - построение суффиксных деревьев. Среди большого количества методов анализа текста метод аннотированного суффиксного дерева выделяется тем,...
-
Липредеры на основе ковариационного метода - Вокодеры с линейным предсказанием
Одними из видов липредеров с низкой скоростью передачи являются липредеры на основе ковариационного метода. Атал и Ханауэр в работах и впервые...
-
В химическом машиностроении нейрокомпьютеры применяются для создания систем управления химическими реакторами, ректификационными колоннами и другими...
-
Геометрический метод, Двойственная задача - Линейное программирование
Применяется для задач с двумя переменными. Метод решения состоит в следующем: На плоскости строятся прямые, которые задают соответствующие ограничения:...
-
Для построения эффективной системы мониторинга необходимо определить объекты наблюдения, отслеживаемые показатели и сроки их представления, программные...
-
Комплектной называют поверку, при которой определяются MX СИ, присущие ему как единому целому. Поэлементной называют поверку, при которой значения MX СИ...
-
Для решения трехмерной задачи упругости с помощью метода конечных элементов были заданы следующие основные параметры: [1]. Количество секций. [2]....
-
Описание разработанных модулей В разработанной программе имеется 5 модулей. Главный модуль "Program. cs" предназначен для запуска главного окна...
-
У рассмотренных ранее программ для трехмерной реконструкции имеются несколько недостатков при вычислении цвета модели. Выражаются они в том, что цвет...
-
Определение методов реинжиниринга информационных систем Основные задачи, которые стоят перед проектировщиком, занимающимся реинжинирингом информационных...
-
Корпоративная интеграционная подсистема на базе IBM WebSphere Business Integration Message Broker [28] отвечает за выстраивание корпоративной...
-
Кратные интегралы, Дифференцирование - Вычисление интегралов в Mathcad
Для того чтобы вычислить кратный интеграл: 1. Введите, как обычно, оператор интегрирования. 2. В соответствующих местозаполнителях введите имя первой...
-
Прогнозируемая оценка проекта после реализации единой шины данных как прослойки между всеми компонентами ИТ-ландшафта компании выполняется по методу...
-
Задание на курсовую работу - Вычисление интегралов в Mathcad
1. Задание 1. 1.1. Постройте и отформатируйте график функции f(x) на заданном отрезке. 1.2 Найти (графически) точки, в которых достигаются наибольшее и...
-
В основе метода EWMA лежит экспоненциальное сглаживание первого порядка [20, 21]: (5.2.1) Где 0<л?1 - константа сглаживания. В роли начального...
-
Вариант №1 1. Выбрать и обосновать наиболее эффективный метод решения задачи. 2. Разработать алгоритм и программу для решения задачи в общем виде. 3....
-
Методы и средства проектирования - Автоматизированные системы обработки экономической информации
Проектирование - процесс создания проекта-прототипа, прообраза предполагаемого или возможного объекта, его состояния. Современная технология создания АИС...
-
Составление частотного уравнения методом последовательного расщепления Рисунок 3.1 - Исходная модель. Расщепим ее на массе 2 Рисунок 3.2 - Расщепление на...
-
Собственными называют периодические колебания консервативной системы, совершающиеся исключительно под воздействием инерционных и упругих сил. Для...
-
Известно, что создание систем "с нуля" приводит к глобальным затратам компании на фонд оплаты труда, на поддержание созданного решения. К тому же, чем...
Методы вычислений