Условие разрешимости транспортной задачи, Особенности ограничений транспортной задачи - Транспортная задача и ее решение методом потенциалов
Теорема. Чтобы транспортная задача была разрешима, необходимо и достаточно, чтобы выполнялось условие:
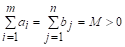
(1.5)
Доказательство:
Необходимость. Пусть транспортная задача разрешима, т. е. система ограничений (1.1) - (1.2) задачи совместна, тогда существуют значения xij (; ), удовлетворяющие этим условиям. Необходимо доказать, что
.
Просуммировав условия (1.2а) по i, а условия (1.2б) - по j, получим:
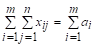
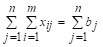
И.
Т. к. левые стороны этих выражений равны, то равны и правые, т. е. , что и требовалось доказать.
Достаточность. Пусть. Необходимо доказать, что существуют значения xij (; ), удовлетворяющие условиям (1.1) - (1.2). Положим
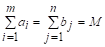
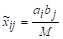
, ;
И покажем, что является планом T. З.
Действительно,
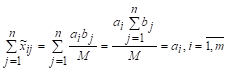
;
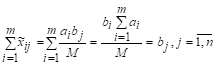
Очевидно также, что
> 0.
Таким образом, условия (1.1) - (1.2) удовлетворяются. Достаточность условий (1.5) доказана.
Особенности ограничений транспортной задачи
T. З. является задачей линейного программирования, и ее можно решить симплексным методом. Однако специфика ограничений T. З. позволяет применять для ее решения методы значительно менее громоздкие, чем симплексный метод. Один из них - метод потенциалов.
Особенности ограничений T. З. следующие:
- А) ограничения заданы в виде уравнений; Б) каждая переменная xij встречается только в двух уравнениях; В) коэффициенты при неизвестных, входящих в уравнение, равны единице (или нулю, если переменные не входят в уравнение).
Рассмотрим систему уравнений (1.2). Она содержит (m + n) уравнений с m - n неизвестными. Сложив почленно уравнения отдельно системы (1.2а) и отдельно - системы (1.2б), мы получим два одинаковых уравнения:
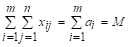
> 0;
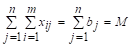
> 0.
Это говорит о том, что система уравнений (1.2) Т. З. линейно зависима и, по крайней мере, одно из уравнений лишнее. Следовательно, максимальное число линейно независимых уравнений системы (1.2), т. е. ранг r системы, не более, чем (m + n - 1).
Можно показать, что ранг r в точности равен (m + n - 1), т. е. система ограничений T. З. содержит ровно (m + n - 1) линейно независимых уравнений. Это означает, что если систему уравнений (1.2) решить методом Жордана-Гаусса, то число базисных переменных будет равно (m + n - 1).
Одним из методов решения T. З., который учитывает специфику ее ограничений, является метод потенциалов. По существу, его можно рассматривать, как результат реализации симплексного метода в условиях транспортной задачи (1.1)-(1.3).
Метод потенциалов состоит из трех шагов.
Первый шаг - отыскание исходного опорного плана перевозок T. З..
Второй шаг - проверка найденного плана на оптимальность. Если условия оптимальности плана перевозок выполнены - задача решена.
Третий шаг - если найденный план не является оптимальным, находим новый опорный план, который ближе к оптимальному, чем предыдущий, и снова переходим к выполнению второго шага.
Таким образом, в методе потенциалов первый шаг выполняется один раз, а второй и третий шаги могут выполняться неоднократно, если исходный план окажется неоптимальным.
Похожие статьи
-
Транспортная задача оптимальность Поставим в соответствие поставщикам потенциалы Ui, , а потребителям - Vj, . В оптимальном плане для всех базисных...
-
Признак оптимальности плана перевозок T. З. устанавливает теорема. Теорема. Для того, чтобы некоторый допустимый план X = (xij)m-nT. З. был оптимальным,...
-
Транспортная задача (Т. З.) является одной из распространенных задач линейного программирования специального вида. Эта задача такого наиболее...
-
Специфика транспортной задачи позволяет находить новое опорное решение задачи и новый базис по правилу более простому, чем в симплекс-методе. Пусть...
-
Вариант №1 1. Выбрать и обосновать наиболее эффективный метод решения задачи. 2. Разработать алгоритм и программу для решения задачи в общем виде. 3....
-
Ранг системы ограничений T. З. равен (m + n - 1), следовательно, невырожденный опорный план Т-задачи содержит (m + n - 1) положительных компонент или...
-
Предложенный подход к решению задач исследования Используя в качестве основы присутствующее в наличии программное обеспечение, которое применимо к...
-
Методика решения задач ЛП графическим методом - Линейное программирование
I. В ограничениях задачи (1.2) заменить знаки неравенств знаками точных равенств и построить соответствующие прямые. II. Найти и заштриховать...
-
Постановка задачи: Для заданных функций необходимо: 1. Построить электронную таблицу (одну для обеих функций) для вычисления значений функций в заданном...
-
Для ускорения процесса конструирования регулятора в пространстве состояний в Matlab была разработана функция, которая, при должной настройке, позволяет...
-
Транспортная задача - Транспортная задача
Сформулировать линейную производственную задачу и составить ее математическую модель, взяв исходные данные из приложения 1, где технологическая матрица А...
-
Анализ предметной области Описание ПО решаемой задачи Предметной областью задачи № 2 также является процесс оплаты денежных средств по кредиту. Решается...
-
Методы Рунге-- Кутты-- важное семейство численных алгоритмов решения обыкновенных дифференциальных уравнений и их систем. Данные итеративные методы...
-
Математический аппарат Для понимания всего дальнейшего полезно знать и представлять себе геометрическую интерпретацию задач линейного программирования,...
-
Дана система линейных уравнений (СЛУ) с n неизвестными: В матричной форме записи система (1) имеет вид: (2) Где : n - порядок системы; - матрица...
-
Теоретические аспекты поставленной задачи В этой части проекта будут объяснены этапы применения МКЭ для плоской фермы. В первой главе было рассмотрено...
-
Геометрический метод, Двойственная задача - Линейное программирование
Применяется для задач с двумя переменными. Метод решения состоит в следующем: На плоскости строятся прямые, которые задают соответствующие ограничения:...
-
"РЕШЕНИЕ ЗАДАЧ ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ С ИСПОЛЬЗОВАНИЕМ MICROSOFT EXCEL" Цель работы Приобретение навыков решения задач линейного программирования...
-
Постановка задачи На стадии оперативного управления возможна замена материалов и комплектующих, указанных в спецификациях, их аналогами. Аналогами...
-
Технические требования Техническое задание данной работы требует разработать программу для визуального редактирования HTML-кода. Программа должна быть...
-
Для того, чтобы разработать оптимальный метод интеграции сторонних систем в существующую ИТ-инфраструктуру систем компании, требуется точно поставить...
-
Пересчет симплекс-таблицы. - Транспортная задача
Формируем следующую часть симплексной таблицы. Вместо переменной x в план 1 войдет переменная x1 . Строка, соответствующая переменной x1 в плане 1,...
-
Выведем в общем виде уравнение движения заданной динамической модели при помощи уравнений Лагранжа II рода. Полная кинетическая энергия: , Полная...
-
Обобщенный алгоритм решения задачи Необходимо рассчитать сумму налога на дарение, воспользовавшись налоговой шкалой. Если сумма подарка менее 80, то она...
-
Постановка задачи Необходимо разработать программу для поиска автобусных маршрутов. В качестве среды разработки должна использоваться Delphi 7. В...
-
Для реализации поставленной задачи методом конечных элементов будут использованы следующие программные обеспечения (ПО): - MATLAB - ПО и одноименный язык...
-
Метод конечных элементов (МКЭ) жесткости возник в аэрокосмической отрасли. Исследователи рассматривали различные подходы к анализу сложных частей...
-
Теоретическая основа линейного программирования, Симплекс метод - Линейное программирование
Симплекс метод Симплекс метод - метод линейного программирования, который реализует рациональный перебор базисных допустимых решений, в виде конечного...
-
Формулировка задачи - Линейное программирование
Даны линейная функция Z=С1 х1 +С2 х2 +...+СN xN (1.1) И система линейных ограничений A11 x1 + a22 x2 +... + a1N ХN = b1 A21 x1 + a22 x2 +... + a2N ХN =...
-
Формирование области многокритериального выбора вариантов Стоит задача о выборе марки автомобиля с их известными особенностями и характеристиками....
-
Библиотека MSHTML MSHTML (так же известен как Trident) - браузерный движок для Microsoft Internet Explorer. Впервые Trident был реализован в четвертой...
-
Заключение. - Приложения технологии системы электронных таблиц Excel к решению задач механики
Целью курсовой работы являлось изучение полного спектра функциональных возможностей технологии системы электронных таблиц Excel. - Задачами данной работы...
-
Групповые имена. - Приложения технологии системы электронных таблиц Excel к решению задач механики
Предположим, что необходимо вычислить сумму целой группы ячеек. Вместо того чтобы перечислять в формуле отдельные ячейки, промаркируйте всю группу и...
-
Табличный процессор Excel фирмы Microsoft предназначен для ввода, хранения, обработки и выдачи больших объемов, данных в виде, удобном для анализа и...
-
Операционная система Windows XP была разработана и выпущена на смену операционной системе DOS фирмой Microsoft XP в 2002 году. Именно поэтому она и...
-
Трудоемкость производство алгоритм excel Трудоемкость годовой производственной программы Трудоемкость по профессии и разряду, ч. 4145,00 Структура...
-
Корпоративная интеграционная подсистема на базе IBM WebSphere Business Integration Message Broker [28] отвечает за выстраивание корпоративной...
-
Обобщенный алгоритм решения задачи Необходимо рассчитать, какую сумму денежных средств внесет лицо, производящее оплату по 1 000 рублей ежеквартально под...
-
Анализ предметной области В задаче № 1 предметной областью является процесс оплаты стоимости чего-либо (продукции или услуги) двумя способами: -...
-
Из основного бизнес-процесса по выполнению заказа на проектирование и конструирование РЭКа можно вынести, что производственную спецификацию проекта отдел...
Условие разрешимости транспортной задачи, Особенности ограничений транспортной задачи - Транспортная задача и ее решение методом потенциалов