Необходимые алгоритмы реализации метода конечных элементов, Теоретические аспекты поставленной задачи - Реализация метода конечных элементов для расчета ферменных конструкций под ОС Android
Теоретические аспекты поставленной задачи
В этой части проекта будут объяснены этапы применения МКЭ для плоской фермы.
В первой главе было рассмотрено понятие фермы - структуры, состоящей из стержневых элементов с двумя узлами, а также определена связь с методом прямой жесткости. Как правило, ферма состоит из 5 или более треугольных единиц, соединенных узлами, определяющими форму конструкции. Внешние силы работают либо на растяжение, либо на сжатие, действуют только в узлах. Деформируемая система в методе конечных элементов представляет собой множество подобластей - конечных элементов, положение определяется конечным числом степеней свободы. Преимущества такого разделения были рассмотрены в первой главе.
Плоская ферма - ферма, где все элементы и узлы лежат в двумерной плоскости, в отличие от пространственной конструкции с тремя измерениями.
Простейшим структурным элементом в МКЭ является двухузловой или линейный элемент. Существуют также элементы, например с шестью или даже 64 узлами, показанными на рисунке 2. Несмотря на это, в методе прямой жесткости все элементы, независимо от сложности, воспринимаются одинаково.
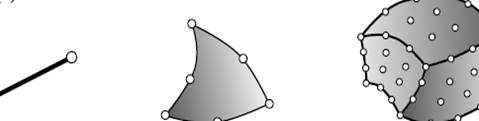
Рис.2. Типы конечных элементов.
Рассмотрение задачи МКЭ для элементов с двумя узлами имеет большие преимущества:
- (А) вычисления могут быть полностью произведены вручную, в отличие от других элементов, представленых выше. Это позволяет понять этапы решения. (Б) относительно простая реализация метода конечных элементов на компьютере на любом языке программирования.
Сначала рассмотрим математическую модель метода для плоской задачи.
Конструкция, представленная на рис.3., имеет три элемента и три узла с координатами X и Y. Также для каждого элемента задаются необходимые параметры: модуль Юнга, характеризующий сопротивление растяжению или сжатию, площадь поперечного сечения, плотность и длина элемента. Задача рассматривается в декартовой системе координат.
Ключевые элементы метода прямой жесткости - усилия f, действующие на узлы и их перемещения u, происходящие под действием этих сил. Силы, действующие на координаты X и Y узла с номером i, обозначаются и соответственно. Аналогично происходит обозначение смещений и. Объединение всех представленных компонентов в вектор представлено ниже, их количество определяет степень свободы системы. В методе прямой жесткости перемещения узлов, определяющих смещение фермы неизвестны.
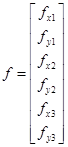
,
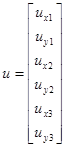
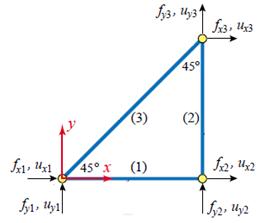
Рис.3. Плоская ферменная конструкция с действующими на нее осевыми усилиями.
Для связи этих векторов необходимо сформировать глобальную матрицу жесткости K для всей ферменной конструкции:
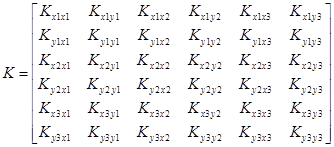
.
Элементы матрицы - коэффициенты жесткости, имеющие определенный смысл. Например, представляет силу по оси Y, действующую на узел 1, при которой возникает смещение второго узла по оси X.
Связывающее уравнение в краткой форме представлено формулой (1):
F = K*U (1).
Рассмотрим этапы решения задач методом прямой жесткости более подробно.
Сначала требуется разбить рассматриваемую конструкцию на элементы. Затем вместе с узлами их нужно пронумеровать. Этот процесс очень важен, поскольку влияет на эффективность вычислений, необходимых для получения решения. Использование МКЭ приводит к системе линейных алгебраических уравнений с большим количеством нулевых коэффициентов. Для плоской задачи все коэффициенты будут лежать между двумя линиями, параллельными главной диагонали матрицы. Расстояние между главной диагональю и этими линиями называется шириной полосы матрицы. Эффективная нумерация приводит к уменьшению размеров требуемой машинной памяти и сокращению времени вычислений. Далее для каждого элемента задается локальной системой координат в виде, где е - номер элемента. (Рис.4-5)
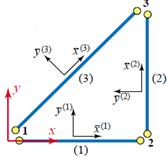
Рис.4.Разделение на элементы и выбор системы координат
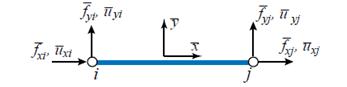
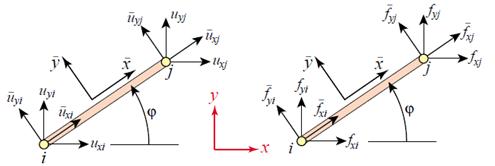
Рис.5.Ферменный элемент с узлами i, j в локальной системе координат.
Из рисунка 5 видно, что элемент плоской ферменной конструкции имеет 4 компонента для узлов и перемещений, то есть 4 степени свободы. Эти компоненты связываются между собой с помощью локальной матрицы жесткости, как показано в полной или краткой формуле (2):
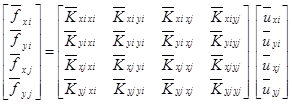
,
. (2)
Вектора и называются узловыми силами и перемещениями для элемента. Разберем построение матрицы.
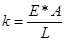
Из механики материалов следует, что жесткость элемента равна,
Где E - модуль Юнга, A - площадь поперечного сечения, L - длина элемента.
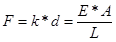
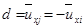
Следовательно, можно записать следующее выражение: , где F - внутреннее осевое усилие, D - Удлинение. В терминах узловых сил и перемещений: , . В итоге получаем матрицу жесткости в локальной системе координат(3):
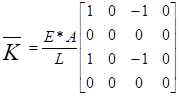
(3)
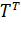
Следующая задача - сформировать из локальных матриц глобальную матрицу жесткости. Так как каждый элемент имеет свою собственную систему координат, то необходимо использовать матрицы поворота T и (транспонированная матрица T) для перемещений и усилий соответственно, чтобы привести все системы к общему виду (рис.4.) .
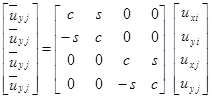
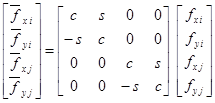
Где с = cos, s = sin.
Рис.4. Поворот элемента на угол в декартовой системе координат.
Пусть е - индекс элемента. Запишем формулу (1) с учетом этого номера:
Также перепишем формулы для вышеуказанных матриц поворота.
,
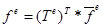
Используя формулу (2), получаем
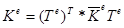
Итак,
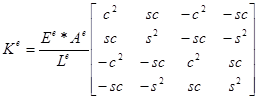
, (4)
Где
Формула(4) определяет глобальную матрицу жесткости для элемента.
Следующий этап - объединение уравнений для каждого элемента в одну глобальную систему. Здесь необходимо учесть два правила:
- 1) объединенные узлы должны двигаться, как единое целое 2) сумма внутренних сил, действующих со стороны всех элементов, которые имеют общий узел, равна внешний силе, действующей на тот же узел.
После этого для каждого элемента к матрице, представленной в формуле(4), добавляются строки и столбцы с нулевыми элементами. Номера добавленных строк и столбцов соответствуют номерам узлов, не принадлежащих этим элементам. Такой способ применяется для ручной работы, на компьютере он является неэффективным из-за большого выделения памяти.
Получив уравнениядля элементов, i определяет номер элемента, записывается общее уравнение для всей ферменной конструкции.
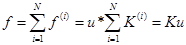
,
Где N - количество элементов.
Поскольку матрица является сингулярной, то для решения уравнений необходимо применить граничные условия. В ручном методе проще всего удалить уравнения, соответствующие нулевым перемещениям. Для компьютерной реализации расширение матрицы не происходит. Она вставляется в свободную таблицу для элементов. Для нулевых перемещений зануляются строки и столбцы, соответствующие нулевым перемещениям и силам и устанавливаются единицы на диагоналях для убирания сингулярности. Если узловое перемещение ненулевое, то исходная система (5) преобразуется в (6). Таким образом, получаем итоговую систему линейных алгебраических уравнений.
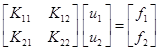
(5)
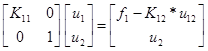
(6)
Завершающий этап вычисления неизвестных перемещений заключается в решении системы. Существует большое множество способом: матричный метод, метод итерации, прогонки и др. Однако метод Гаусса является самым наглядным и простым из всех вариантов. В дальнейшем, именно он будет использоваться для реализации МКЭ.
В пространственной задаче метода прямой жесткости алгоритм действия аналогичен за небольшим исключением: матрица поворота записывается в виде:
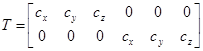
,
Где
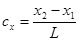
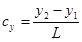
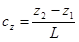
,,,
А глобальная матрица жесткости:
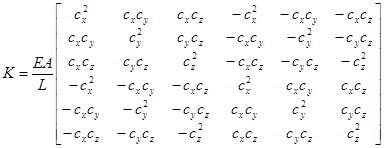
[13][14][15][16][17].
Похожие статьи
-
Наиболее распространенной реализацией МКЭ является метод прямой жесткости, применяемый для компьютерного моделирования сложных структур. Это матричный...
-
Метод конечных элементов является численным методом для нахождения приближенных решений физических задач. В основе этого метода лежит разделение...
-
Метод конечных элементов (МКЭ) жесткости возник в аэрокосмической отрасли. Исследователи рассматривали различные подходы к анализу сложных частей...
-
Ферменная конструкция представляет собой стержневую систему. При замене жестких узлов шарнирами, она остается геометрически неизменяемой и удовлетворяет...
-
Для решения трехмерной задачи упругости с помощью метода конечных элементов были заданы следующие основные параметры: [1]. Количество секций. [2]....
-
С помощью диалоговых окон были отображены задания, их выбор, поля для ввода входных данных, заполняемые по умолчанию, полученный результат и визуализация...
-
Для реализации поставленной задачи методом конечных элементов будут использованы следующие программные обеспечения (ПО): - MATLAB - ПО и одноименный язык...
-
Рассмотрим особенности программирования под Android. Класс Activity - самый важный класс, из которого строится приложение Android. Этот класс...
-
На основе двухмерной задачи упругости методом прямой жесткости была произведена реализация трехмерного случая в программном обеспечении MATLAB и Android...
-
Конечно-элементный анализ широко применяется при решении задач механики деформируемого твердого тела, теплообмена, гидро - и газодинамики, электро - и...
-
Исходным объектом для применения МЮ является материальное тело (в общем случае - область, занимаемая сплошной средой или полем), которое разбивается на...
-
Составление частотного уравнения методом последовательного расщепления Рисунок 3.1 - Исходная модель. Расщепим ее на массе 2 Рисунок 3.2 - Расщепление на...
-
Для того, чтобы разработать оптимальный метод интеграции сторонних систем в существующую ИТ-инфраструктуру систем компании, требуется точно поставить...
-
Управление дорожным движением осуществляется адаптивной компьютерной системой, которая, измеряя реальные потоки транспорта на дороге, оптимизирует...
-
Принцип реализации СЛАУ на кластере - Администрирование параллельных процессов
Метод Гаусса - широко известный прямой алгоритм решения систем линейных уравнений, для которых матрицы коэффициентов являются плотными. Если система...
-
Входная информация разделяется на условно-постоянную и оперативно-учетную информацию. - Условно-постоянная информация включает в себя справочные данные о...
-
Библиотека MSHTML MSHTML (так же известен как Trident) - браузерный движок для Microsoft Internet Explorer. Впервые Trident был реализован в четвертой...
-
В работе возникает необходимость выбора предметной области, в которой будет тестироваться каскадный классификатор. Главными вопросами на данном этапе...
-
Понятие KPI "Ключевые показатели эффективности (англ. Key Performance Indicators, KPI) -- показатели деятельности подразделения (предприятия), которые...
-
Российская система здравоохранения: текущее состояние, основные проблемы и барьеры для дальнейшего развития Российское здравоохранение на сегодняшний...
-
Обоснование выбранного метода При дизайне системы согласно требованиям или при оптимизации существующей необходимо ввести модель, позволяющую не только...
-
Как наука информатика имеет одну главную цель - применение ВМ для поиска нового знания. Собственной целью информатики является знание о знании, структуре...
-
Для решения задачи №3 необходимо ввести исходные данные в электронную таблицу, т. е. таблицы 1,2 (рисунок 16). Рисунок 16 - Ввод исходных данных в...
-
Транспортная задача оптимальность Поставим в соответствие поставщикам потенциалы Ui, , а потребителям - Vj, . В оптимальном плане для всех базисных...
-
, Алгоритм обратного хода: Шаг 1. Вычислим Шаг 2. Вычислим: , Рис. 1. Основной алгоритм решения СЛУ методом исключения Гаусса. Для контроля правильности...
-
Теорема. Чтобы транспортная задача была разрешима, необходимо и достаточно, чтобы выполнялось условие: (1.5) Доказательство: Необходимость. Пусть...
-
Коэффициенты квадратной матрицы А и вектора b Таблица 1 - Коэффициенты квадратной матрицы А и вектора b № Вар Коэффициенты квадратной матрицы А и вектора...
-
Подход NoSQL - Технологии больших данных: анализ и выбор решения для реализации проекта
Понятие NoSQL означает "Не только SQL" или "Не SQL". Термин получил известность, начиная с 2009 год, когда развитие интернет-технологий и социальных...
-
Решим следующую систему методом Гаусса. - Составление программы для решения системы уравнений
A 11 = 2 0. (1) Для решения систем уравнения с помощью Гаусса будем выделить коэффициенты системы следующим образом: A 11 =2, A 12 = 7, a 13 =13 b 1 = 0...
-
Программная модель данных, получившая название "MapReduce", была создана несколько лет назад в компании Google, и там же была осуществлена первая...
-
Методы и средства проектирования - Автоматизированные системы обработки экономической информации
Проектирование - процесс создания проекта-прототипа, прообраза предполагаемого или возможного объекта, его состояния. Современная технология создания АИС...
-
Собственными называют периодические колебания консервативной системы, совершающиеся исключительно под воздействием инерционных и упругих сил. Для...
-
Обобщенный алгоритм решения задачи Необходимо рассчитать, какую сумму денежных средств внесет лицо, производящее оплату по 1 000 рублей ежеквартально под...
-
Моделирования случайных процессов - Теоретические основы информационных технологий
Моделирование случайных процессов - мощнейшее направление в современном математическом моделировании. Событие называется случайным, если оно достоверно...
-
Понятие о компьютерном математическом моделировании Модель - материальный объект, система математических зависимостей или программа, имитирующая...
-
Структура кластера и его параметры Вычислительный кластер -- это совокупность компьютеров, объединенных в рамках некоторой сети для решения одной задачи,...
-
Постановка задачи нечеткого управления Была рассмотрена задача по прогнозированию износа (в микрометрах) тормозных дисков автомобилей. Входные данные:...
-
В задаче деформирования после определения глобального вектора степеней свободы {U} находят элементные векторы узловых перемещений {U}E. Через них путем...
-
Система Windows NT не является дальнейшим развитием ранее существовавших продуктов. Ее архитектура создавалась с нуля с учетом предъявляемых к...
-
Для определения выплат по займу используется финансовая функция ПЛТ (Ставка, КПер, Пс, Бс, Тип). Определим значения параметров функции ПЛТ: Ставка =9%...
Необходимые алгоритмы реализации метода конечных элементов, Теоретические аспекты поставленной задачи - Реализация метода конечных элементов для расчета ферменных конструкций под ОС Android