Условия Фукса - Условия Фукса и теорема Пенлеве
Интегралы уравнения вида
(1)
Не имеют критических подвижных точек.
Если в раскрытом виде уравнение (1)
(2)
И если содержит w, то интегралы уравнения (2) имеют подвижные критические точки.
Уравнения с неподвижными критическими точками рассматриваемого типа имеют вид
,
Причем все суть многочлены относительно w степени не выше 2k.
Переходим теперь к изучению разложения. Пусть разложение имеет вид
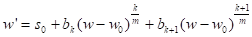
+..., (3)
Где, причем здесь. Сделаем замену, откуда. Подставляя в уравнение (3), получим для W уравнение
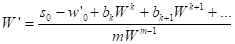
. (4)
Рассмотрим сначала случай, когда не равно тождественно нулю. В этом случае для интеграла уравнения (4), обращающегося в нуль при, имеем следующее разложение:
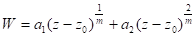
+..., (5)
Причем, если.
Подставляя разложение (5) в (4) и затем в уравнение (3), получим
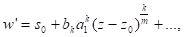
Причем степень дальнейших членов разложения выше. Отсюда, интегрируя, получим, что если k не делится без остатка на m, то w имеет в критическую алгебраическую точку.
Итак, для отсутствия критических подвижных точек необходимо, чтобы было целое число; подобным же образом докажем, что и все следующие члены правой части уравнения (3) содержат в степенях с целыми показателями.
В случае разложений вида (3) с дробными показателями у при, не равном тождественно нулю, интегралы уравнения (1) имеют подвижные критические точки.
Следовательно, для того, чтобы уравнение (1) было уравнением с неподвижными критическими точками, необходимо, чтобы
. (6)
Но есть результат исключения w' из уравнений
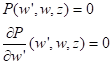
То есть функция, определяемая из дискриминантного уравнения D(w, z)=0.
Уравнение (6) показывает, что в рассматриваемом случае удовлетворяет уравнению (1).
Интегралы уравнения, которые получаются из дискриминантного уравнения, как известно, называются особыми интегралами. Отсюда получаем следующий важный результат.
Если уравнение вида (1) есть уравнение с неподвижными критическими точками, то все решения дискриминантного уравнения суть особые интегралы.
Если, то уравнение (4) принимает вид
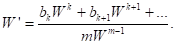
(7)
Если, то уравнение (7), а также и уравнение (3) имеют голоморфный интеграл, определяемый начальным значением при.
Рассмотрим случай, когда. В этом случае уравнение (7) можно написать в виде
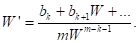
(8)
Фукса пенлеве теорема
Интеграл уравнения (13), обращающийся в нуль при, имеет вид
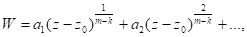
(9)
Причем.
Отсюда получим для правой части уравнения (3) разложение вида
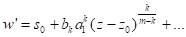
, (10)
Причем коэффициенты зависят от и при произвольном отличны от нуля.
Интегрируя уравнение (10), получим, что w имеет в критическую алгебраическую точку. Итак, для отсутствия критических подвижных точек необходимо, чтобы.
Сопоставляя вместе все найденные выше результаты, получим следующую теорему, доказанную впервые Фуксом.
Для того, чтобы уравнение вида
,
Где (w, z) - многочлены относительно w, не имело критических подвижных точек, должны выполняться следующие условия:
- 1) (w, z) не должно содержать w и является, следовательно, функцией только от z; таким образом, деля обе части уравнения на, можно его всегда привести к такому виду, что ; 2) степень относительно w не должна превосходить 2k; 3) решения дискриминантного уравнения D(w, z)=0 должны являться интегралами данного уравнения; 4) если разложение w' в области решения дискриминантного уравнения имеет вид
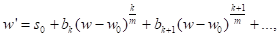
То должно выполняться неравенство.
Заметим, что теорема Фукса дает условия, необходимые и достаточные для отсутствия в интегралах критических алгебраических особых точек.
Похожие статьи
-
Теорема Пенлеве - Условия Фукса и теорема Пенлеве
Все приведенные выше исследования велись в предположении, что мы изучаем поведение интеграла в области изменения z, при котором w(z) принимает вполне...
-
Математик-циклоп - Великая теорема Ферма
Создание математики -- занятие мучительное и таинственное. Объект доказательства часто бывает ясен, но путь к доказательству теряется в тумане, и...
-
Дуэль с бесконечностью - Великая теорема Ферма
Чтобы доказать Великую теорему Ферма, Уайлсу было необходимо сначала доказать гипотезу Таниямы-Шимуры о том, что каждой эллиптической кривой можно...
-
Следствия теоремы, Послесловие к доказательству - Об одной теореме теории чисел
Не существует ЦЕЛЫХ чисел, для которых выполняется равенство (1). При четных значениях показателя степени уравнение вида (1) идентично как для...
-
Исходная задача: При ограничениях: Двойственной является следующая задача: При ограничениях: Число неизвестных в двойственной задаче равно 2....
-
Принцип сходимости, Предел функции. Теорема Гейне - Свойства функций
Рассмотрим вопрос о существовании пределов последовательностей концевых точек бесконечной системы промежутков, вложенных друг в друга. Лемма Кантора ....
-
Доказательство теоремы Ферма Уважаемый Григорий Яковлевич! Обращается к Вам Черепанов Николай Михайлович, математик из Барнаула. В 2004 году, я...
-
Вводим дополнительные ограничения в модель: А) продукция типа 1 выпускается только в том случае, если разрешен выпуск хотя бы одного типа продукции: 2 и...
-
Запечатанные конверты - Великая теорема Ферма
После прогресса, достигнутого благодаря работам Софи Жермен, Французская Академия Наук установила серию премий, включая золотую медаль и 3000 франков,...
-
Теоремы Ферма, Ролля, Лагранжа и Коши
Введение В данном реферате рассматриваются теоремы Ферма, Ролля, Лагранжа и Коши. "Теорема - высказывание, нравственность которого установлена при помощи...
-
Моделирование в условиях противодействия, игровые модели - Основы теории систем и системного анализа
Как уже неоднократно отмечалось, системный анализ невозможен без учета взаимодействий данной системы с внешней средой. Ранее упоминалась необходимость...
-
Сущность и основные условия применения корреляционного анализа В соответствии с сущностью корреляционной связи ее изучение имеет две цели: 1) измерение...
-
В большинстве реальных больших систем не обойтись без учета "состояний природы" -- воздействий Стохастического типа, случайных величин или случайных...
-
Ангидритным способом в лабораторных условиях Разложение фосфата серной кислотой проводим согласно уравнению реакции: Ca3(PO4)2 + 3H2SO4 > 3CaSO4(тв)...
-
Актуальность темы. В современных условиях глобальной конкуренции на все более интегрирующихся мировых рынках, развитие химической промышленности...
-
В реальных производственных условиях, во-первых, не может быть мгновенных поставок партий исходного продукта переработки, а во-вторых, технологический...
-
Эндрю Уайлс во время обучения в колледже. Тайные вычисления - Великая теорема Ферма
"Однажды вечером, в конце лета 1986 года, я попивал чай в гостях у своего приятеля. В беседе он между прочим упомянул о том, что Кену Рибету удалось...
-
Моделирование системы в условиях неопределенности - Основы теории систем и системного анализа
Как уже отмечалось в первой части нашего курса, в большинстве реальных больших систем не обойтись без учета "состояний природы" -- воздействий...
-
Месье Леблан - Великая теорема Ферма
К началу XIX века за Великой теоремой Ферма установилась устойчивая репутация самой трудной проблемы в теории чисел. После прорыва, осуществленного...
-
Анализ условий образования эффективных объединений предприятий молочного подкомплекса АПК
Анализ условий образования эффективных объединений предприятий молочного подкомплекса АПК Несбалансированный процесс взаимоотношений между...
-
Введение, История теоремы - Великая теорема Ферма
Она заинтересовала меня тем, что на вид очень простая и казалось бы, решить ее может каждый школьник, но найти ее решение на протяжении 358 лет пытались...
-
Доказательство теоремы - Об одной теореме теории чисел
Доказательство теоремы проводится отдельно для случая, когда (т. е. показатель степени в равенстве (2) - НЕЧЕТНОЕ число) и когда (т. е. показатель...
-
Наличие особых ситуаций на террайне зависит от характеристик его сложности. Ниже приведена возможная классификационная схема характеристик сложности...
-
Синтаксис и семантика. Теорема Райса - Рекурсивные функции
Попробуем теперь проанализировать круг проблем, неразрешимость которых доказана в предыдущем пункте. Общим для них является то, что по кодам, т. е....
-
Заключение - Планирование деятельности предприятия в условиях рынка
Планирование будет действенным только в том случае, если оно будет отвечать следующим требованиям: Во-первых, планирование должно отвечать на вопросы:...
-
В теории чисел большую роль играет числовая функция, называемая функцией Эйлера. Определение 3.1. Функцией Эйлера называется функция, определенная на...
-
Теорема 1. Предел постоянной равен самой постоянной. . Доказательство. f(x)=с, докажем, что . Возьмем произвольное e>0. В качестве d можно взять любое...
-
Условия существования гамильтонова цикла - Гамильтоновы циклы
В отличие от эйлеровых графов, где имеется критерий для графа быть эйлеровым, для гамильтоновых графов такого критерия нет. Более того, задача проверки...
-
Знаменитая теория полимолекулярной адсорбции Брунауэра, Эммета и Теллера, получившая название теории БЭТ (по первым буквам фамилий ученых), основана на...
-
Выводы, Литература - Методика теоретико-игрового обоснования условий проведения конкурса
1. Разработанная методика теоретико-игрового обоснования условий проведения конкурса позволяет при оценке возможных действий неопределенных факторов...
-
- одношаговость процедуры (для Субъектов); - Субъекты - участники конкурса не образуют коалиции и не обмениваются информацией о поданных предложениях, но...
-
Реакции ионного обмена - это реакции между ионами, образовавшимися в результате диссоциации электролитов. Правила составления ионных уравнений реакций 1....
-
Рождение проблемы - Великая теорема Ферма
Жизненно важным, поворотным пунктом в развитии западной математики стал 1453 год, когда турки разграбили Константинополь. За прежние годы рукописи,...
-
Создатель Великой проблемы - Великая теорема Ферма
Пьер де Ферма родился 20 августа 1601 года в городе Бомон-де-Ломань на юго-западе Франции. Его отец, Доминик Ферма, был состоятельным торговцем кожей,...
-
Химическое строение, физико-химические и физические свойства лекарственных средств Свойства лекарственных средств в значительной степени обусловлены их...
-
В 1930 году Дж. Биркгофом и Дж. фон Нейманом была сформулирована и доказана одна из основных эргодических теорем - теорема о предельных вероятностях:...
-
В данной работе доказывается методами элементарной математики "большая" или "последняя" теорема Ферма. Некоторая, излишняя в обычных случаях, подробность...
-
Условие задачи - Расчет электрической цепи
Два электродвигателя переменного тока подключены параллельно к цепи с напряжением U2 И работают с низким коэффициентом мощности cos1. Измерительные...
-
Теорема об универсальной функции - Рекурсивные функции
Для любого n, nN, универсальная функция u(n) вычислима. Доказательство. При доказательстве мы можем ограничиться случаем N=1. Действительно, программу,...
-
Теорема о параметризации - Рекурсивные функции
Одно и то же выражение может порождать несколько разных функций, от разного числа аргументов. Так, обычное арифметическое выражение xK можно считать...
Условия Фукса - Условия Фукса и теорема Пенлеве