Условия существования гамильтонова цикла - Гамильтоновы циклы
В отличие от эйлеровых графов, где имеется критерий для графа быть эйлеровым, для гамильтоновых графов такого критерия нет. Более того, задача проверки существования гамильтонова цикла оказывается NP-полной. Большинство известных фактов имеет вид: "если граф G имеет достаточное количество ребер, то граф является гамильтоновым". Приведем несколько таких теорем.
Теорема Дирака. Если в графе G (V, E) c n вершинами (n ? 3) выполняется условие d(v) ? n/2 для любого vV, то граф G является гамильтоновым.
Доказательство.
От противного. Пусть G - не гамильтонов. Добавим к G минимальное количество новых вершин u1, ..., uN, соединяя их со всеми вершинами G так, чтобы G':= G + u1 + ... + uN был гамильтоновым.
Пусть v, u1, w, ..., v - гамильтонов цикл в графе G', причем vG, u1G', u1G. Такая пара вершин v и u1 в гамильтоновом цикле обязательно найдется, иначе граф G был бы гамильтоновым. Тогда wG, w {u1,..., uN}, иначе вершина u1 была бы не нужна. Более того, вершина v несмежна с вершиной w, иначе вершина u1 была бы не нужна.
Далее, если в цикле v, u1, w, ..., u', w', ..., v есть вершина w', смежная с вершиной w, то вершина v' несмежна с вершиной v, так как иначе можно было бы построить гамильтонов цикл v, v', ..., w, w', ..., v без вершины u1, взяв последовательность вершин w, ..., v' в обратном порядке. Отсюда следует, что число вершин графа G', не смежных с v, не менее числа вершин, смежных с w. Но для любой вершины w графа G d(w) ? p/2+n по построению, в том числе d(v) ? p/2+n. Общее число вершин (смежных и не смежных с v) составляет n+p-1. Таким образом, имеем:
N+p-1 = d(v)+d(V) ? d(w)+d(v) ? p/2+n+p/2+n = 2n+p.
Следовательно, 0 ? n+1, что противоречит тому, что n > 0.
Теорема Оре. Если число вершин графа G (V, E) n ? 3 и для любых двух несмежных вершин u и v выполняется неравенство:
D(u)+d(v) ? n и (u, v)E, то граф G - гамильтонов.
Граф G имеет гамильтонов цикл если выполняется одно из следующих условий:
Условие Поша: D(vK) ? k+1 для k < n/2.
Условие Бонди: из d(vi) ? i и d(vk) ? k => d(vi)+d(vk)?n (k?i)
Условие Хватала: из d(vK) ? k ? n/2 => d(vN-k) ? n-k.
Далее, известно, что почти все графы гамильтоновы, то есть
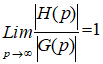
Где H(p) - множество гамильтоновых графов с p вершинами, а G(p) - множество всех графов с p вершинами. Таким образом, задача отыскания гамильтонова цикла или эквивалентная задача коммивояжера являются практически востребованными, но для нее неизвестен (и, скорее всего не существует) эффективный алгоритм решения.
Пример графа, когда не выполняется условие теоремы Дирака, но граф является гамильтоновым.
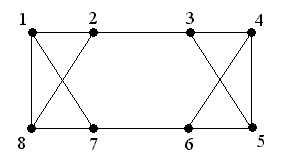
N = 8; d(vI) = 3; 3 ? 8/2 = 4 не гамильтонов граф, но существует гамильтонов цикл: M = (1, 2, 3, 4, 5, 6, 7, 8, 1)
Похожие статьи
-
Гамильтоновы циклы, Основные понятия и определения - Гамильтоновы циклы
Название "гамильтонов цикл" произошло от задачи "Кругосветное путешествие" предложенной ирландским математиком Вильямом Гамильтоном в 1859 году. Нужно...
-
Пока неизвестно никакого простого критерия или алгебраического метода, позволяющего ответить на вопрос, существует или нет в произвольном графе G...
-
Задачи, связанные с поиском гамильтоновых циклов - Гамильтоновы циклы
В ряде отраслей промышленности возникает следующая задача планирования. Нужно произвести n продуктов, используя единственный тип аппаратуры. Аппарат...
-
Наличие особых ситуаций на террайне зависит от характеристик его сложности. Ниже приведена возможная классификационная схема характеристик сложности...
-
Теорема: Для того, чтобы ограниченная на сегменте функция была интегрируемой на этом сегменте, необходимо и достаточно, чтобы для любого нашлось такое...
-
Для монополии ситуация на рынке обстоит иначе, чем на совершенном конкурентном рынке. Так как монополист является единственным производителем товара,...
-
Ангидритным способом в лабораторных условиях Разложение фосфата серной кислотой проводим согласно уравнению реакции: Ca3(PO4)2 + 3H2SO4 > 3CaSO4(тв)...
-
Неопределенность - это фундаментальное свойство природы, а еще более (и точнее) - свойство, характеризующее неточность, незамкнутость, неокончательность,...
-
Сущность и основные условия применения корреляционного анализа В соответствии с сущностью корреляционной связи ее изучение имеет две цели: 1) измерение...
-
Условия Фукса - Условия Фукса и теорема Пенлеве
Интегралы уравнения вида (1) Не имеют критических подвижных точек. Если в раскрытом виде уравнение (1) (2) И если содержит w, то интегралы уравнения (2)...
-
Принцип сходимости, Предел функции. Теорема Гейне - Свойства функций
Рассмотрим вопрос о существовании пределов последовательностей концевых точек бесконечной системы промежутков, вложенных друг в друга. Лемма Кантора ....
-
Моделирование в условиях противодействия, игровые модели - Основы теории систем и системного анализа
Как уже неоднократно отмечалось, системный анализ невозможен без учета взаимодействий данной системы с внешней средой. Ранее упоминалась необходимость...
-
Пусть ограничения (4) не противоречивы, т. е. не пусто множество допустимых решений, а оптимальное решение достигается я в точке для каждой K -ой...
-
Вводим дополнительные ограничения в модель: А) продукция типа 1 выпускается только в том случае, если разрешен выпуск хотя бы одного типа продукции: 2 и...
-
1. Предпосылки метода наименьших квадратов. 2. Проблема мультиколлинеарности. 3. Гомоскедатичность и гетероскедатичность. Линейные регрессионные модели с...
-
Теорема Пенлеве - Условия Фукса и теорема Пенлеве
Все приведенные выше исследования велись в предположении, что мы изучаем поведение интеграла в области изменения z, при котором w(z) принимает вполне...
-
- одношаговость процедуры (для Субъектов); - Субъекты - участники конкурса не образуют коалиции и не обмениваются информацией о поданных предложениях, но...
-
Число непосредственных участников конкурса - число субъектов , Где - множество Субъектов, - обозначение мощности множества. В качестве рассматривается...
-
Введение, Основные положения - Эволюционные процедуры решения комбинаторных задач на графах
Среди набора комбинаторно-логических задач на графах важное место занимает проблема определения паросочетаний, раскраски графа, выделения в графе...
-
О квази-клике. - Использование квази-клик для анализа графа рынка России
Квази-клика - представляет собой релаксацию строгого условия полноты клики, то есть допускается отсутствие некоторых ребер в искомом подграфе. На данный...
-
Анализ условий образования эффективных объединений предприятий молочного подкомплекса АПК
Анализ условий образования эффективных объединений предприятий молочного подкомплекса АПК Несбалансированный процесс взаимоотношений между...
-
О клике. Определим формально задачу поиска максимальной клики, согласно статьи On the maximum quasi-clique problem [17]. Пусть G=(V, E) - простой...
-
Адсорбционные методы исследования свойств поверхности позволяют количественно охарактеризовать происходящие при адсорбции межмолекулярные взаимодействия,...
-
В большинстве реальных больших систем не обойтись без учета "состояний природы" -- воздействий Стохастического типа, случайных величин или случайных...
-
В данной работе доказывается методами элементарной математики "большая" или "последняя" теорема Ферма. Некоторая, излишняя в обычных случаях, подробность...
-
Моделирование системы в условиях неопределенности - Основы теории систем и системного анализа
Как уже отмечалось в первой части нашего курса, в большинстве реальных больших систем не обойтись без учета "состояний природы" -- воздействий...
-
Выводы, Литература - Методика теоретико-игрового обоснования условий проведения конкурса
1. Разработанная методика теоретико-игрового обоснования условий проведения конкурса позволяет при оценке возможных действий неопределенных факторов...
-
РЕШЕНИЕ ЗАДАЧИ О КОММИВОЯЖЕРЕ МЕТОДОМ ВЕТВЕЙ И ГРАНИЦ: ОСНОВНАЯ СХЕМА - Задача коммивояжера
Пусть - конечное множество и - вещественно-значная функция на нем; требуется найти минимум этой функции и элемент множества, на котором этот минимум...
-
Хлебопродуктовый кооперация производственный технологический Согласно классической модели Харриса, рассматривается непрерывное расходование запасов и...
-
Опыт проводили в условиях, имитирующих периодическую экстракцию: в стакан одновременно загружали все реагенты и перемешивают их в течение заданного...
-
Актуальность темы. В современных условиях глобальной конкуренции на все более интегрирующихся мировых рынках, развитие химической промышленности...
-
Необходимое условие идентификации Уравнение 1: H=3 D+1=H Уравнение идентифицируемое D=2 Уравнение 2: H=3 D+1=H Уравнение идентифицируемое D=2 Уравнение...
-
Сходящиеся последовательности, Основные свойства сходящихся последовательностей: - Свойства функций
Говорят, что Последовательность сходится, если существует число такое, что для любого существует такое , что для любого , выполняется неравенство: ....
-
ОПРЕДЕЛЕНИЕ МЕТОДА ФАКТОРНОГО АНАЛИЗА И ЧИСЛА ФАКТОРОВ - Многомерный статистический анализ
Определение метода факторного анализа. Различные методы факторного анализа различаются в зависимости от подходов, которые используются для выделения...
-
Основные процессы СЭС представлены комплексом направлений деятельности, которые можно представить как EP(t)={EP1(t), EP2(t) ... EPN(t)},, где i=1..n, n -...
-
Функционирование СЭС предусматривает соблюдение четких требований к направлениям ее деятельности. Требуется разработать математический аппарат оценки...
-
Введение - Методика теоретико-игрового обоснования условий проведения конкурса
Важным аспектом любой деятельности государственных и муниципальных субъектов является организация и проведение конкурсов на поставки товаров, выполнение...
-
Реакции ионного обмена - это реакции между ионами, образовавшимися в результате диссоциации электролитов. Правила составления ионных уравнений реакций 1....
-
Технические условия на ХММ. Характеристика исходного сырья, химикатов Таблица 1 ХММ типа "ОПКО" Технические условия Наименование показателя Ед. изм. ХММ...
-
Задача кластеризации может быть сведена к задаче раскраски вершин графа. Для этого строится граф несовместимости. Вершинам графа соответствуют...
Условия существования гамильтонова цикла - Гамильтоновы циклы