Интегральная теорема Муавра-Лапласа
Предположим, что в условиях схемы Бернулли проводится испытаний, в результате каждого из которых с вероятностью () происходит событие. Интегральная теорема Муавра-Лапласа содержит приближенную формулу для вероятности того, что событие появится не менее раз и не более раз. С ростом количества испытаний числа и растут, а вероятность постоянна.
Теорема. Если Вероятность События В Каждом Испытании Постоянна И Отлична Как От Нуля, Так И От Единицы, То Вероятность Того, Что Событие Появится В Испытаниях От До Раз, Приближенно Равна Определенному Интегралу:
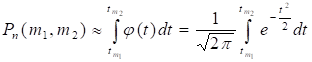
,
Доказательство. На основании теоремы сложения вероятности для несовместных событий:
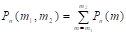
.
Отсюда, используя локальную теорему Лапласа:
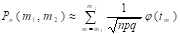
,
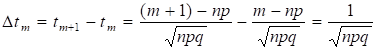
Поскольку,
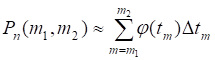
Следовательно.
Причем, эта сумма является интегральной для функции на отрезке, так как при, т. е. при, ее предел равен соответствующему определенному интегралу:
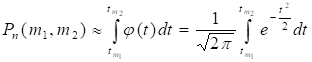
,
Что и требовалось доказать.
Введем стандартный интеграл Лапласа (функцию Лапласа):
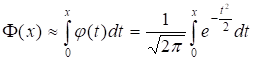
,
Который, очевидно, является первообразной Функции Гаусса:
Тогда на основании формулы Ньютона - Лейбница можно записать
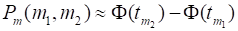
.
Значения функций и обычно находятся из таблиц, причем таблицы обычно даны лишь для неотрицательных значений, поскольку - четная функция, а - нечетная. Из таблиц видно, что при значения практически не отличаются от 0.5, поэтому далее табуляция, как правило, не ведется.
Пример 1.
Небольшой город ежедневно посещают 100 туристов, которые днем идут обедать. Каждый из них выбирает для обеда один из двух городских ресторанов с равными вероятностями и независимо друг от друга. Владелец одного из ресторанов желает, чтобы с вероятностью приблизительно 0,99 все пришедшие в его ресторан туристы могли там одновременно пообедать. Сколько мест должно для этого быть в его ресторане?
Решение. Будем считать, что событие произошло, если турист пообедал у заинтересованного владельца. По условию задачи, . Нас интересует такое наименьшее число посетителей, что вероятность одновременного прихода не менее чем туристов из числа с вероятностью успеха приблизительно равна вероятности переполнения ресторана, т. е.
Таким образом, нас интересует такое наименьшее число. Применим интегральную теорему Муавра-Лапласа.
В нашем случае: - неизвестно, . Тогда:
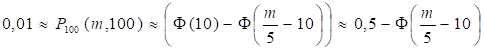
Используя таблицы для функции, находим, и, значит, . Следовательно, в ресторане должно быть 62 места.
Точность формул Муавра-Лапласа сильно зависит от соотношения величин и : она существенно увеличивается с ростом произведения. Обычно этими формулами пользуются, когда. Однако, в случае близости одной из величин или к нулю (другая в это время мало отличается от единицы) возникает необходимость в значительном увеличении числа испытаний.
Пример 2.
Вероятность того, что деталь не прошла проверку ОТК, равна р=0,2. Найти вероятность того, что среди 400 случайно отобранных деталей окажется непроверенных от 70 до 100 деталей.
Решение. По условию, р=0,2; ; ; ; . Воспользуемся интегральной теоремой Лапласа:
Вычислим нижний и верхний пределы интегрирования:
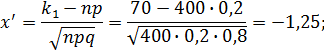
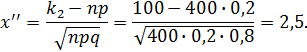
Теорема вероятность муавр лаплас
Таким образом, имеем:
По таблице приложения 2 находим:
Искомая вероятность
Пример 3.
Симметричная монета подбрасывается 1000 раз. Найти вероятность того, что число выпавших орлов будет лежать в пределах от 487 до 507.
Решение Применим теорию Лапласа:
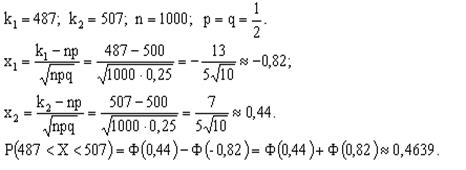
Пример 4.
Найти вероятность того, что из 1000 новорожденных будет от 456 до 545 мальчиков, если вероятность рождения мальчика равна 0,515.
Решение. x2 =1.898, x1 =-3.797.
P=0.5(Ф(1,898)+Ф(3,797))=0,9711.
Пример 5.
Вероятность того, что деталь не прошла проверку отклонений равна 0,2. Найти вероятность, что среди 400 отобранных деталей непригодных окажется от 70 до 100.
Решение.
Воспользуемся интегральной теоремой Лапласа.
P400(70,100)?Ц(100?400-0.2v400-0.2-0.8)?Ц(70?400-0.2v400-0.2-0.8)=Ц(2.5)+Ц(1.25)
Ц(2.5)=0.4958;Ц(1.25)=0.3944 (табличные данные)
P400(70,100)=0.4958+0.3944=0.8882
Похожие статьи
-
Пусть - один и тот же опыт повторяется n-раз, не зависимо от результатов; в любом опыте может наступить событие А с вероятностью p, либо событие A с...
-
Свойство 1. Вероятность достоверного события равна единице. Действительно, если событие достоверно, то каждый элементарный исход испытания...
-
Теоремы Ферма, Ролля, Лагранжа и Коши
Введение В данном реферате рассматриваются теоремы Ферма, Ролля, Лагранжа и Коши. "Теорема - высказывание, нравственность которого установлена при помощи...
-
Интегральная и дифференциальная функции распределения - Основы научных исследований
Наиболее общей формой задания распределения случайных величин является Интегральная функция распределения . Она определяет вероятность того, что...
-
В теории чисел большую роль играет числовая функция, называемая функцией Эйлера. Определение 3.1. Функцией Эйлера называется функция, определенная на...
-
ОПРЕДЕЛЕННЫЕ ИНТЕГРАЛЫ, Интегральные суммы - Определенные интегралы
Интегральные суммы Пусть функция задана на сегменте, . Обозначим символом разбиение сегмента при помощи некоторых несовпадающих друг с другом точек на...
-
Принцип сходимости, Предел функции. Теорема Гейне - Свойства функций
Рассмотрим вопрос о существовании пределов последовательностей концевых точек бесконечной системы промежутков, вложенных друг в друга. Лемма Кантора ....
-
Теорема 1. Предел постоянной равен самой постоянной. . Доказательство. f(x)=с, докажем, что . Возьмем произвольное e>0. В качестве d можно взять любое...
-
В 1930 году Дж. Биркгофом и Дж. фон Нейманом была сформулирована и доказана одна из основных эргодических теорем - теорема о предельных вероятностях:...
-
В данной работе доказывается методами элементарной математики "большая" или "последняя" теорема Ферма. Некоторая, излишняя в обычных случаях, подробность...
-
Ответ: y=f(kx) получается из Графика функции f(x) сжатием его вдоль оси ох в k раз, если k>1 и растяжением в 1 деленную на k раз, если k>0 но меньше 1....
-
Математик-циклоп - Великая теорема Ферма
Создание математики -- занятие мучительное и таинственное. Объект доказательства часто бывает ясен, но путь к доказательству теряется в тумане, и...
-
Рождение проблемы - Великая теорема Ферма
Жизненно важным, поворотным пунктом в развитии западной математики стал 1453 год, когда турки разграбили Константинополь. За прежние годы рукописи,...
-
Введение, История теоремы - Великая теорема Ферма
Она заинтересовала меня тем, что на вид очень простая и казалось бы, решить ее может каждый школьник, но найти ее решение на протяжении 358 лет пытались...
-
Симплекс - метод - Интегральное и дифференциальное исчисление
Другой способ решения задач линейного программирования - симплекс-метод. Он, в отличие от геометрического, является полностью аналитическим, что...
-
Пусть на некотором отрезке [a, b] задана кусочно-монотонная функция f(x). Покажем, что данную функцию в точках ее непрерывности можно представить в виде...
-
Доказательство теоремы Ферма Уважаемый Григорий Яковлевич! Обращается к Вам Черепанов Николай Михайлович, математик из Барнаула. В 2004 году, я...
-
Исходная задача: При ограничениях: Двойственной является следующая задача: При ограничениях: Число неизвестных в двойственной задаче равно 2....
-
Эра загадок и головоломок - Великая теорема Ферма
С античных времен и поныне математики пытались придать занимательность своим учебникам, излагая теоремы и доказательства в форме решений числовых...
-
Запечатанные конверты - Великая теорема Ферма
После прогресса, достигнутого благодаря работам Софи Жермен, Французская Академия Наук установила серию премий, включая золотую медаль и 3000 франков,...
-
Месье Леблан - Великая теорема Ферма
К началу XIX века за Великой теоремой Ферма установилась устойчивая репутация самой трудной проблемы в теории чисел. После прорыва, осуществленного...
-
Синтаксис и семантика. Теорема Райса - Рекурсивные функции
Попробуем теперь проанализировать круг проблем, неразрешимость которых доказана в предыдущем пункте. Общим для них является то, что по кодам, т. е....
-
Теорема Клини о нормальной форме - Рекурсивные функции
Существуютпримитивнорекурсивныефункция u и примитивно разрешимый предикат T такие, что e, x ( E(x)=p ( k [T(e, x,k)])). В частности, e, x ( E(x) k T(e,...
-
У цьому параграфі узагальнюються і уточнюються так звані "зворотні теореми" теорії наближення. Мова йде про оцінці диференціальних властивостей функції f...
-
Уход в абстракцию - Великая теорема Ферма
После работ Эрнста Куммера надежды найти доказательство ослабли, как никогда прежде. Кроме того, в математике начали развиваться различные новые области....
-
Создатель Великой проблемы - Великая теорема Ферма
Пьер де Ферма родился 20 августа 1601 года в городе Бомон-де-Ломань на юго-западе Франции. Его отец, Доминик Ферма, был состоятельным торговцем кожей,...
-
Геометрический метод - Интегральное и дифференциальное исчисление
Теоретическое введение: Применяется, как правило, для задач линейного программирования, содержащих не более 2 переменных. Суть геометрического метода...
-
Алгоритмы метода Монте-Карло для решения интегральных уравнений второго рода Пусть необходимо вычислить линейный функционал , Где, причем для...
-
Следствия теоремы, Послесловие к доказательству - Об одной теореме теории чисел
Не существует ЦЕЛЫХ чисел, для которых выполняется равенство (1). При четных значениях показателя степени уравнение вида (1) идентично как для...
-
Теория: Применяется, как правило, для задач линейного программирования, содержащих не более 2 переменных. Суть геометрического метода сводится к...
-
Введение - Приложение интегрального и дифференциального исчисления к решению прикладных задач
Целью данной курсовой работы является самостоятельное изучение следующих разделов высшей математики: задачи линейного программирования (симплексный и...
-
Доказательство теоремы - Об одной теореме теории чисел
Доказательство теоремы проводится отдельно для случая, когда (т. е. показатель степени в равенстве (2) - НЕЧЕТНОЕ число) и когда (т. е. показатель...
-
В потемках - Великая теорема Ферма
Уайлс, о котором мир тогда еще ничего не знал, с облегчением вздохнул. Великая теорема Ферма по-прежнему оставалась непобежденной, и он мог продолжать...
-
Награда Эндрю - Великая теорема Ферма
Предложенное Уайлсом доказательство Великой теоремы Ферма опирается на доказательство гипотезы, родившейся в 50-е годы XX века. Его рассуждения...
-
Снова великая теорема Ферма! - Великая теорема Ферма
Сегодня в доказательстве великой теоремы Ферма произошел поистине поразительный сдвиг. Наум Элькис (профессор Гарвардского университета) заявил, что...
-
"Доказана ли Великая теорема Ферма?" - Великая теорема Ферма
Был сделан лишь первый шаг на пути к доказательству гипотезы Таниямы-Шимуры, но избранная Уайлсом стратегия была блестящим математическим прорывом,...
-
Эндрю Уайлс во время обучения в колледже. Тайные вычисления - Великая теорема Ферма
"Однажды вечером, в конце лета 1986 года, я попивал чай в гостях у своего приятеля. В беседе он между прочим упомянул о том, что Кену Рибету удалось...
-
Теорема о параметризации., Универсальные функции - Рекурсивные функции
Любую часть x1,x2,...,xn входных значений можно породить программно, более того - существует алгоритм, который генерирует по x1,x2,...,xn текст...
-
Специфика интегрированной производственной системы (ИПС) АПК, как объекта исследования риска, выражается в том, что она может включать несколько...
-
Симплекс-метод - Приложение интегрального и дифференциального исчисления к решению прикладных задач
Теория: Другой способ решения задач линейного программирования - симплекс-метод. Он, в отличие от геометрического, является полностью аналитическим, что...
Интегральная теорема Муавра-Лапласа