Симплекс - метод - Интегральное и дифференциальное исчисление

Другой способ решения задач линейного программирования - симплекс-метод. Он, в отличие от геометрического, является полностью аналитическим, что позволяет использовать его в задачах с практически любым конечным числом переменных. Для его использования все ограничения задачи должны представлять собой равенства. Чтобы добиться этого обычно вводят дополнительные переменные. Симплекс-метод основан на том, что оптимальным решением ЗЛП является какая-либо вершина многогранника допустимых решений ЗЛП. Вначале выбирается произвольно любая вершина многогранника (иногда это может быть сопряжено с определенными трудностями). Затем осуществляется переход к другим вершинам до тех пор, пока не обнаруживается оптимальная. Необходимо отметить, что главной отличительной чертой симплекс-метода по сравнению с простым перебором является то, что переход к следующей вершине осуществляется в направлении роста (или падения) целевой функции. Это позволяет значительно ускорить процесс поиска оптимального решения.

В основе симплексного метода решения ЗЛП лежит метод последовательных исключений.

Добавляем к левой части неравенств некоторую неотрицательную величину Ui>=0.

X1>=0, X2>=0, Ui>=0 (i=1,2,3)

Целевая функция: 4X1+3X2+0U1+0U2+0U3max

Причем каждому решению системы неравенств (1.0) соответствует единственное решение системы уравнений и неравенств (1.1).

2. Записываем Гауссову таблицу.

X1	X2	U1	U2	U3	B
2	3	1	0	0	60
6	1	0	1	0	60
2	1	0	0	1	24

3. Записываем симплекс-таблицу.

4	3	0	0	0
X1	X2	U1	U2	U3	B
0	U1	2	3	1	0	0	60
0	U2	6	1	0	1	0	60
0	U3	2	1	0	0	1	24
-4	-3	0	0	0	0

В первой строке записываются коэффициенты целевой функции при соответствующих переменных второй строки.

В втором столбце записываются переменные, находящиеся в базисе.

В первом столбце записываются коэффициенты целевой функции переменных, находящихся в базисе.

Последняя строка - индексная. Ее элементы вычисляются по формуле

БS= s-й столбец*1 столбец - число, стоящее в 1 строке и s-м столбце.

Одновременно с этим последний элемент индексной строки является значением целевой функции.

У нас в базисе U1, U2, U3.

Опорное решение: (0;0;60;60;24). Fmax=0

Симплексное преобразование выполняется по следующему правилу:

1) Выбираем разрешающий столбец, соответствующий наибольшему по модулю отрицательному элементу в индексной строке. 2) Выбирается разрешающая строка, которая соответствует наименьшему положительному из отношений элементов правой части уравнений на соответствующие элементы разрешающего столбца. На пересечении разрешающей строки и разрешающего столбца стоит разрешающее число. 3) Элементы разрешающей строки делятся на разрешающее число. 4) Вычисляются элементы всех остальных строк по формуле:

Новые эл-ты = старые эл-ты -

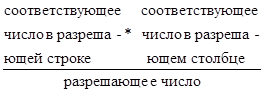
С каждым последующим симплексным преобразованием значение целевой функции будет увеличиваться. При этом:

1) Если в индексной строке найдется хотя бы один отрицательный элемент и - в разрешающем столбце найдется хотя бы один положительный элемент, то можно улучшить решение; - разрешающий столбец не содержит положительных элементов, то целевая функция неограниченно возрастает. 2) Если все элементы индексной строки неотрицательны, то достигнуто оптимальное решение.

Это и есть достаточные условия существования оптимального плана решения.

4. В нашем случае: наибольшее по модулю отрицательное число в индексной строке стоит в 1 столбце, следовательно разрешающий столбец 1. Разрешающая строка 2.

Вводим в базис X1 вместо U2.

4	3	0	0	0
X1	X2	U1	U2	U3	B
0	U1	0	1	-	0	40
4	X1	1	0	0	10
0	U3	0	0	-	1	4
0	-	0	0	40

В базисе U1, X1, U3.

Новое опорное решение: (10; 0; 40; 0; 4) Fmax=40

Решение не является оптимальным, т. к. в индексной строке есть отрицательные элементы.

5. Наибольшее по модулю отрицательное число в индексной строке стоит во 2 столбце, следовательно разрешающий столбец 2. Разрешающая строка 3.

Вводим в базис X2 вместо U3.

4	3	0	0	0
X1	X2	U1	U2	U3	B
0	U1	0	0	1	1	-4	24
4	X1	1	0	0	-	9
0	X2	0	1	0	-	6
0	0	0	-	54

В базисе X1, X2, U1.

Опорное решение: (9; 6; 24; 0; 0), Fmax=54.

Решение не является оптимальным, т. к. в индексной строке есть отрицательные элементы.

6. Наибольшее по модулю отрицательное число в индексной строке стоит в 4 столбце, следовательно разрешающий столбец 4. Разрешающая строка 1.

Вводим в базис U2 вместо U1.

4	3	0	0	0
X1	X2	U1	U2	U3	B
0	U2	0	0	1	1	-4	24
4	X1	1	0	-	0	3
0	X2	0	1	0	-	18
0	0	0	66

В базисе U1, X1, X2.

Опорное решение: (3; 18; 0; 24; 0), Fmax=66.

Данное решение является оптимальным, т. к. в индексной строке отсутствуют отрицательные элементы.

Ответ: оптимальный план 3 свадебных торта и 18 праздничных тортов. Fmax=66.

Задание №3

Разложить в ряд Фурье по синусам функцию

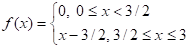
Теоретическое введение:

Определение. Функциональный ряд вида

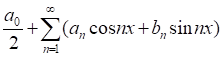
Называется тригонометрическим рядом или рядом Фурье. Постоянные числа a0, an, и bn (n=1,2,...) называются коэффициентами тригонометрического ряда или коэффициентами Фурье.

Если дана периодическая функция f(x) с периодом 2р, то целью применения ряда Фурье является отыскание тригонометрического ряда, сходящегося к данной функции. Таким образом, мы отыскиваем функцию, являющуюся суммой ряда в интервале (-р, р):

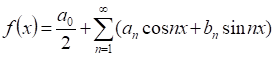
При этом коэффициенты Фурье находят по формулам:

, ,

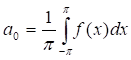
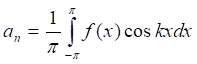
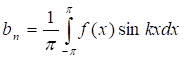
О разложении в ряд Фурье непериодической функции. Пусть на некотором отрезке [a, b] задана кусочно-монотонная функция f (x). Покажем, что данную функцию в точках ее непрерывности можно представить в виде суммы ряда Фурье. Для этого рассмотрим произвольную периодическую кусочно-монотонную функцию f1 (x) с периодом 2м ? b - a, совпадающую с функцией f (x) на отрезке [a, b].

Разложим функцию f1 (x) в ряд Фурье. Сумма этого ряда во всех точках отрезка [a, b] (кроме точек разрыва) совпадает с заданной функцией f (x), т. е. мы разложили функцию

F (x) в ряд Фурье на отрезке [a, b].

Решение:

Разложим исходную функцию f (x) в ряд Фурье по синусам на отрезке [0, 3].

;

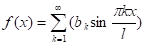
Ответ:

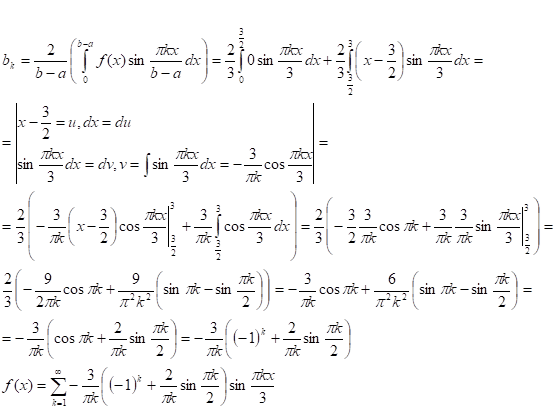
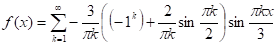
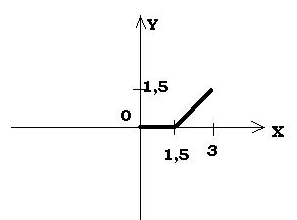
А) Нарисовать график функции ѓ(x) на отрезке [0;3]

Теоретическое введение :

Определение. Функция f(x) назыВАется Кусочно-монотонной на отрезке, если этот отрезок можно разбить конечным числом точек на интервалы так, что на каждом из интервалов функция монотонна, т. е. либо невозрастающая, либо неубывающая.

Решение:

Из этого определения следует, что данная функция является кусочно монотонной, т. к. на интервалах (0;1,5) и (1,5;3) она монотонна.

Б) Написать, к чему сходится этот ряд в точках отрезка [0,3].

Теоретическое введение:

Определение. Функция f (x) называется удовлетворяющей условиям Дирихле на сегменте [a, b], если: функция непрерывна на сегменте [a, b] или же имеет на нем конечное число точек разрыва 1 рода; функция кусочно-монотонна на сегменте [a, b].

Теорема Дирихле: Пусть периодическая функция f (x) с периодом 2р удовлетворяет на любом сегменте условиям Дирихле. В таком случае ряд Фурье, соответствующий этой функции, сходится во всех точках числовой оси. При этом в каждой точке непрерывности функции f (x) сумма ряда S (x) равна значению функции в этой точке. В каждой точке x0 разрыва функции сумма ряда равна среднему арифметическому предельных значений функции при x>x0 слева и справа, т. е.:

S(x) = 0,5[f(x0 + 0)+f(x0 - 0)]

Решение:

Внутри интервала (0;3) ряд сходится к значениям самой функции f(x).

S(0)=

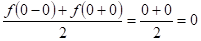
S(3)=

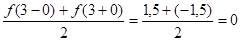
В) Нарисовать график суммы ряда на отрезке [-3,9].

Практическая часть:

В каждой точке x0 разрыва функции сумма ряда равна среднему арифметическому предельных значений функции при x>x0 слева и справа.

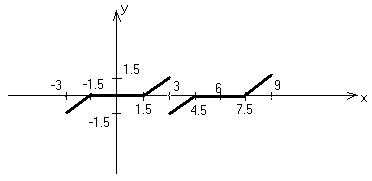
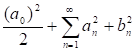
Г) Пользуясь равенством Парсеваля найти сумму: .

Теоретическое введение:

Для функции f(x), такой, что f2(x)L(-;), справедливо равенство Парсеваля:

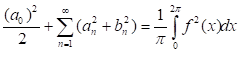
Решение:

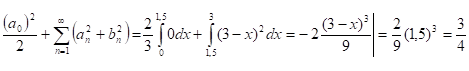
Ответ : 0,75.

Задание №4

Найти линейную комбинацию функций 1, x, x2+3x+3 дающую наилучшее приближение по норме функции f(x) = x3+3x2+2x+3 на отрезке [-1,1].

Указание: ортогонализировать данную систему функций и воспользоваться экстремальным свойством коэффициентов Фурье.

Теоретическая часть:

Определение. Скалярным произведением двух кусочно-непрерывных на функций будем называть интеграл.

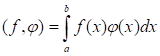
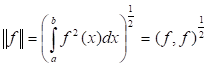
Определение. Величина называется Нормой функции F.

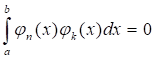
Определение. Система кусочно-непрерывных на отрезке [a, b] функций (конечная или бесконечная) называется Ортогональной, если при любых n ? k выполняется равенство(т. е. функции попарно ортогональны) и функции имеют положительную норму.

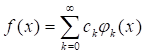
Пусть функция F(x), определенная на отрезке [a, b], такова, что: .При этом:

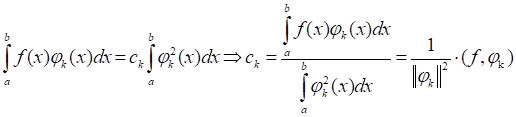
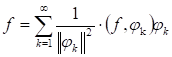
Коэффициенты, вычисленные по данной формуле называют коэффициентами Фурье функция F(x) По системе ортогональных функций. А ряд называют рядом Фурье функция F(x) по ортогональной системе функций.

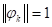
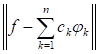
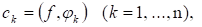
Теорема. Если система функций Ц1(x), ц2(x), ..., цN(x) ортонормирована(), то для любой функции F норма среди всевозможных систем чисел достигает своего минимума для единственной системы чисел, определяемых равенствами т. е. для коэффициентов Фурье функции F.

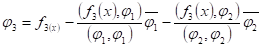
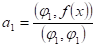
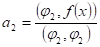
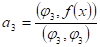
Решение:

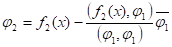
L1(x)=1

L2(x)=x

L3(x)= x2+3x+3

Ортогонализируем данную систему фукций:

1. f1(x)=L1=1 2. f2(x)=бf1+L2, причем б подбираем таким образом, чтобы (f1;f2)=0

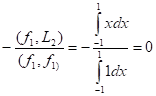
Б =

F2(x)=x

3. f3(x)=вf2 + гf1 + L3, причем в и г подбираем так, чтобы (f3;f1)=0 и (f3;f2)=0

Г =

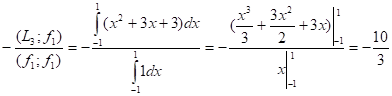
В =

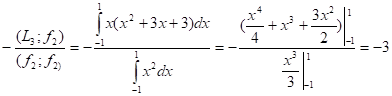
F3 = -3x - + x2 + 3x + 3 = x2 - 1/3

4. f1(x)= 1

f2(x)= x

f3(x)= x2 - 1/3

5. Воспользуемся экстремальным свойством коэффициентов Фурье:

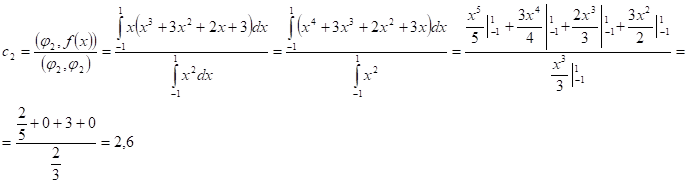
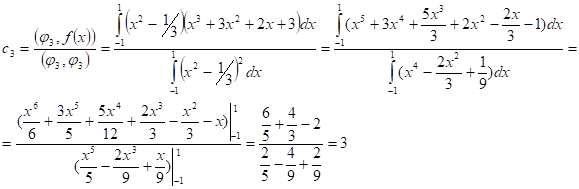
Отсюда,

F(x) = c1F1 + c2F2 + c3F3 = 4 + 2,6x + 3(x2 - 1/3) = 3x2 + 2,6x +3.

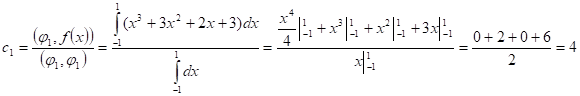
Ответ: F(x)= 3x2 + 2,6x +3

Задание №5

Найти объем тела, ограниченного поверхностями:

9(x2 + y2) >= 16z2

X2 + y2 + z2 <= 25

Z<=0

Теоретическое введение:

Пусть в пространстве задана некоторая область V, ограниченная замкнутой поверхностью S. Пусть в области V и на ее границе определена некоторая непрерывная функция F(x, y, z), где X, y, z - прямоугольные координаты точки области. Для ясности в случае, если F(x, y, z)0, мы можем считать эту функцию плотностью распределения некоторого вещества в области V.

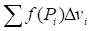
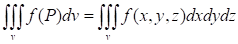
Разобьем область V произвольным образом на области, обозначая символом не только самую область, но и ее объем. В пределах каждой частичной области выберем произвольную точку и обозначим через значение функции F в этой точке. Составим интегральную сумму вида (1) и будем неограниченно увеличивать число малых областей так, чтобы наибольший диаметр стремился к нулю. Если функция F(x, y, z) непрерывна, то при этом будет существовать предел интегральных сумм вида (1). Этот предел, не зависящий ни от способа разбиения области V, ни от выбора точек, обозначается символом (2) и называется тройным интегралом.

Если подынтегральная функция F(x, y, z)=1, то тройной интеграл по области V выражает объем области V:

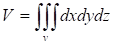
Декартовы прямоугольные координаты:

Вычисление тройного интеграла в декартовых прямоугольных

Координатах сводится к последовательному вычислению одного однократного и одного

Двойного интегралов. Если область интегрирования ограничена снизу и сверху соответственно поверхностями:

А с боков - прямым цилиндром, сечением которого плоскостью, параллельной плоскости X0Y является область D, то:

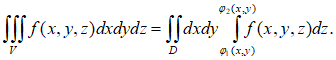
Вычисление начинаем с внутреннего интеграла

По переменной z, считая переменные x и y константами, а затем вычисляем двойной интеграл по проекции области V на плоскость X0Y.

Симплекс - метод - Интегральное и дифференциальное исчисление

Похожие статьи