Информационная оценка технологического совершенства сложных иерархических схем - Методы информационного анализа материальных процессов
При общей характеристике энтропийно-информационного анализа любых объектов широко используется статистическая формула Шеннона для выражения неопределенности любой системы:
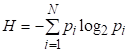
, (2.23)
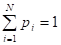
Где РI - вероятность обнаружения какого-либо однородного элемента системы в их множестве ; , [30].
Мы рассмотрим применение данной формулы для количественной оценки неопределенности качества продукта или технологического передела через неопределенность главного элемента системы. В качестве вероятности обнаружения главного элемента технологической системы можно принять его содержание в продукте, выраженное в долях единицы. То же самое относится и к процессу извлечения элемента в тот или иной продукт, так как в этом случае показатель извлечения тождествен вероятности перехода данного элемента из одного состояния системы в другое состояние. Для оценки качества продукта или технологических переделов могут быть в равной степени использованы оба этих показателя - содержание и извлечение.
До опубликования созданной К. Шенноном теории Р. Хартли предложил определять количество информации по формуле:
, (2.24)
Где - количество информации; - число элементов системы [11].
Собственной информацией назовем вещественную функцию операций обнаружения или извлечения элементов, зависящую только от вероятностей операций и удовлетворяющую следующим условиям:
- 1 , 2 ,
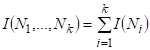
3 .
Выразим количество информации или неопределенности через известные функции. Поскольку информация должна зависеть только от вероятности процессов, нам надо найти на отрезке функцию с вещественными значениями, которая будет удовлетворять условиям 1-3. Легко видеть, что если монотонно убывает на отрезке и, то условия 1,2 выполнены. Остается найти условие на, обеспечивающее выполнение условия 3.
Пусть имеется два независимых технологических процесса и. Тогда из условия аддитивности 3 следует:
,
И поскольку по теореме умножения вероятностей независимых событий выполняется равенство:
,
Условие 3 равносильно выполнению соотношения:
.
Таким образом, функция должна удовлетворять функциональному уравнению:
.
То, что монотонные решения полученного уравнения исчерпываются кратными натурального логарифма - это классический результат. Поэтому мы должны взять, где. Эта функция обращается в нуль при для любого значения константы. Итак, если мы определим соотношением:
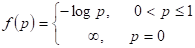
,
То функция, заданная равенством, обладает всеми свойствами неопределенности.
Ранее руководителем были сформулированы и доказаны следующие теоремы (2.1-2.9). Мною они использованы для проведения дальнейших научных исследований в этом аспекте.
Теорема 2.1 Пусть собственная информация элементов технологической системы, состоящей из элементов, равна:
. (2.25)
Тогда информационная энтропия данного дискретного множества определяется равенством:
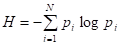
, (2.26)
Из определения случайной величины можно заключить о целесообразности принять собственную информацию элементов системы за дискретную случайную величину, а ее среднее значение, или математическое ожидание, за информационную энтропию.
Для множества элементов, принимающих конечное число значений:
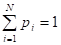
, (2.27)
Собственная информация определяется равенством:
[31]. (2.28)
Теорема 2.2 Если множество дискретных вероятностных распределений имеет элементов, то информационная энтропия конечного дискретного вероятностного распределения удовлетворяет условию:
.
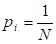
Более того, тогда и только тогда, когда дискретное множество содержит элемент вероятности единица, и тогда и только тогда, когда дискретное множество имеет равномерное распределение, то есть, [31,32].
Следствие 1 Информационная энтропия альтернативного выбора из двух равновероятных возможностей равна:
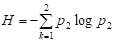
. (2.29)
Информационная энтропия обладает свойствами:
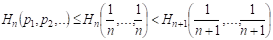
Следствие 2 Энтропия непрерывного множества элементов вычисляется по формуле:
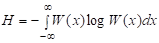
, (2.30)
Где - плотность распределения величины, представляющей непрерывное множество одномерного пространства событий.
Для энтропийно-информационного анализа технологического передела необходимо выбрать единую меру статистических и детерминистических начал в любом целом. Наиболее полно эта мера выражается в информации, которая может быть выражена в различных отношениях: свободная и связанная, субъективная и объективная, реальная и потенциальная и т. д. Столь же правомерно использование энтропии как меры неупорядоченности, которая также охватывает весь спектр состояний системы, включая полную упорядоченность.
Информация, как мера определенности, отражает функцию структурного начала в технологической системе, а энтропия, как мера неопределенности, ее бесструктурного дополнения [31].
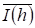
Теорема 2.3 Если, - Относительные значения информации, энтропии и на основании закона сохранения суммы энтропии и информации выполнено условие:
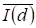
, (2.31)
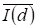
То есть решение уравнения:
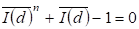
, (2.32)
В работах показано, что на основании закона сохранения максимума энтропии выполняется равенство:
(2.33)
По условию теоремы имеем:
, (2.34)
Где, - относительное значение информации и энтропии [33].
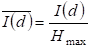
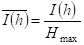
Задача нахождения корней уравнения (2.31) решается в два этапа. Прежде чем переходить к решению уравнения (2.31), запишем его в виде:
, (2.35)
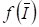
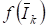
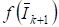
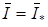
И отметим два простых приема отделения действительных корней уравнения (2.35). Предположим, что функция определена и непрерывна на отрезке. Первый прием состоит в том, что вычисляется таблица значений функции в заданных точках. Если обнаружится, что при некотором числа, имеют разные знаки, то это будет означать, что на интервале уравнение (2.35) имеет по крайней мере один действительный корень. Затем можно разбить интервал на более мелкие интервалы и с помощью аналогичной процедуры уточнить расположение корня. Более регулярным способом отделения действительных корней является метод бисекции или деления пополам]. Можно использовать прием выделения корней, а именно, если корень кратности найден, то рассматривается функция:
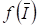
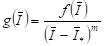
И для нее повторяется процесс нахождения корня.
Для нахождения решений уравнения (2.35) рассмотрим метод простой итерации. Для этого заменим уравнение (2.35) уравнением:
. (2.36)
Итерации в данном случае образуются с заданным начальным приближением по правилу:
, (2.37)
Где
Для сходимости большое значение имеет выбор функции. Ее можно задавать различными способами. Пусть функция имеет вид:
, (2.38)
Причем функция не меняет знака на отрезке, где отыскивается корень.
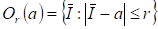
Теорема 2.4 Для того, чтобы уравнение (2.36) имело единственное решение на отрезке, необходимо выполнение условий:
1 Липшиц-непрерывности функции с постоянной в области :
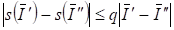
, (2.39)
Где, - отрезок, длины с серединой в точке.
1 Удовлетворение неравенству:
. (2.40)
Причем, решение разностной задачи стремится к решению исходной задачи со скоростью:
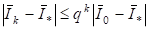
.
Мы установили, что рассмотренный итерационный метод удовлетворяет всем требованиям, предъявляемым к численным методам для нахождения корней алгебраических многочленов [34].
Математическое описание процесса развития любой системы, а значит и технологической, задается формулой:
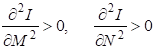
, (2.41)
Где - масса технологической системы; - число элементов системы.
Положительная вторая производная свидетельствует об ускоренном развитии системы, суть которого состоит в том, что при переходе на более высокий структурный уровень технологического процесса вступает в действие закон или принцип прогрессивного увеличения разнообразия. В математическом понимании принцип увеличения разнообразия состоит в том, что с переходом на более высокие структурные уровни число элементов, образующих данный структурный уровень, имеющий различные признаки, увеличивается по закону:
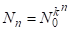
, (2.42)
Где N - порядковый номер, рассматриваемого уровня, ; - число элементов N - го уровня технологической системы; - длина кода элементов на каждом уровне иерархической системы; - число элементов уровня технологической системы, принятого за начало отсчета n=0.
Более строго этот принцип выразится следующим образом:
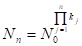
. (2.43)
Пусть - число элементов N - го уровня иерархической системы, . - есть емкость информации нулевого уровня. Тогда емкость информации N - го уровня в расчете на один элемент выражается формулой:
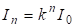
, (2.44)
Где K - длина кода элементов на каждом уровне иерархической системы.
Используя свойства логарифмической функции, получим:
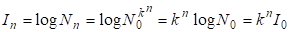
. (2.45)
Непосредственная математическая взаимосвязь между этими двумя подходами к выявлению оптимальных соотношений стохастической и детерминированной составляющих отсутствует. Если в первом из них устанавливается динамика системы неравенствами (2.41), то во втором на основе уравнения (2.35) - статика системы. В связи с этим поставим задачу получения статических решений из динамических условий (2.41). В этом случае для механического роста накопления информации должны выполняться условия теоремы 2.5.
Теорема 2.5 Для получения статических решений из динамических условий необходимо выполнение следующих условий:
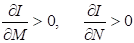
, (2.46)
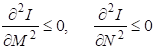
. (2.47)
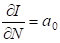
Рассмотрим развитие технологической системы поэтапно, начиная с нулевого уровня. Введем обозначение - скорость накопления информации на нулевом уровне, тогда на основании теоремы 2.5:
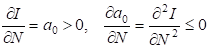
. (2.48)
При переходе на первый уровень технологической схемы должен произойти скачок по условию (2.41). Накопление информации в пределах этого уровня должно подчиняться условию механического роста, иначе не будет объективной необходимости перехода на следующий уровень технологического передела. Следовательно, рост информации на первом уровне выражается формулой:
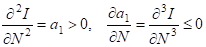
, (2.49)
Где - скорость накопления информации на первом уровне.
Используя метод математической индукции, можно определить условия роста информации на любом уровне технологического передела [31,34].
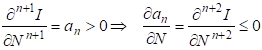
, (2.50)
Где - скорость накопления информации на N - ом уровне.
В рассматриваемой нами иерархической системе смежные уровни технологического передела отличаются по темпу накопления информации на один порядок производной. Справедлива теорема 2.6
Теорема 2.6 Пусть накопление информации на каждом уровне технологического передела происходит без замедления (ускорения), то есть выражается равенством:
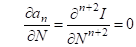
. (2.51)
Тогда общий темп накопления информации на каждом уровне:
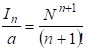
, (2.52)
А общее количество информации есть сумма информаций, присущих каждому уровню технологического передела:
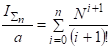
, (2.53)
Где - скорость накопления информации, постоянная на всех уровнях.
Возьмем интеграл от обеих частей равенства (2.51) и, учитывая, что скорость накопления информации на каждом уровне технологического процесса положительна, получим:
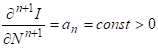
. (2.54)
Таким образом, на каждом уровне есть величина постоянная и не зависит от, что позволяет рассмотреть уравнение (2.51) как обыкновенное дифференциальное уравнение.
Отмеченные особенности выражений (2.52) и (2.53) относятся к общим свойствам иерархических систем при условии равной скорости накопления информации на каждом уровне технологического передела [31,32].
Похожие статьи
-
Детерминация по Седову, Сороко, Малышеву - Методы информационного анализа материальных процессов
Одной из важнейших работ, в которой дан анализ энтропийно-информационных характеристик различного вида систем, является монография Е. А. Седова "Эволюция...
-
Количество информации по Шеннону и Хартли. Связь между ними Определение количества информации по Шеннону требует с самого начала привлечения...
-
Энтропия по Клаузиусу. Формулы Больцмана и Планка Во второй половине XX века произошли два события, которые в значительной мере определяют дальнейшие...
-
Анализировать общие механизмы энтропийно-информационных закономерностей материальных процессов, являющихся фундаментальной основой всех самопроизвольно...
-
Введение - Методы информационного анализа материальных процессов
Обоснование необходимости проведения данной дипломной работы. Использование меры определенности и неопределенности информации позволяет анализировать...
-
Рассмотрим основные идеи, лежащие в основе колмогоровского определения количества информации. Введение колмогоровской меры имеет основной целью уточнение...
-
В качестве примера модели, в основе которой лежит уравнение матфизики, рассмотрим модель распространения тепла в однородном стрежне. Задача...
-
Элементы матричного анализа - Методы решения системы линейных уравнений
Вектором, как на плоскости, так и в пространстве, называется направленный Отрезок , то есть такой Отрезок , один из концов которого выделен и называется...
-
РЕШЕНИЕ ЗАДАЧИ О КОММИВОЯЖЕРЕ МЕТОДОМ ВЕТВЕЙ И ГРАНИЦ: ОСНОВНАЯ СХЕМА - Задача коммивояжера
Пусть - конечное множество и - вещественно-значная функция на нем; требуется найти минимум этой функции и элемент множества, на котором этот минимум...
-
Общая схема метода Монте-Карло Сущность метода Монте-Карло состоит в следующем: требуется найти значение а некоторой изучаемой величины. Для этого...
-
В промышленности синтез глиоксаля окислением этиленгликоля протекает в адиабатических условиях, оптимальный температурный режим процесса зависит от...
-
Монте карло погрешность распределение интеграл В качестве оценки интеграла принимают , Где n - число испытаний; F(x) - плотность распределения...
-
Метод дихотомии требует менее всего итераций цикла для получения корней уравнения с заданной точностью. Если расчет ведется без помощи ЭВМ, то это...
-
Метод Гомори последовательных отсечений - Математическое моделирование экономических процессов
При решении многих задач (планирование мелкосерийного производства, распределение кораблей по путям сообщения, выработка суждений типа "да-нет" и т. п.)...
-
Элементы технологических схем производства формальдегида на оксидном катализаторе (рисунок 1.3 и 2.2) не совпадают, поскольку программная система Hysys...
-
Нysys Эта программа предназначена для технологических расчетов. С помощью программы Hysys можно разрабатывать адекватные стационарные и динамические...
-
Использование современных информационно-коммуникационных технологий в образовательном учреждении позволяет решить ряд фундаментальных задач: Внедрить...
-
Термодинамика процесса В процессах парофазного каталитического окисления моноатомных спиртов и этиленгликоля возможна реализация следующих превращений...
-
Один из способов повысить селективность - это правильно подобрать катализатор. Рассмотрим этот метод, на примере получения анизола и крезола. Анизол и...
-
Качественные методы анализа - Разработка технологической схемы получения анизола и крезола
Рециркуляционных реакционно-ректификационных процессов. При анализе сложных ХТС, характеризующихся большим числом параметров и переменных необходимо...
-
Исходная задача: При ограничениях: Двойственной является следующая задача: При ограничениях: Число неизвестных в двойственной задаче равно 2....
-
Некоторые особенности решения задач нелинейного программирования - Экономико-математические методы
Для решения ЗНП существенно знать: 1) выпукло или не выпукло множество допустимых решений задачи; 2) является ли целевая функция выпуклой или вогнутой...
-
Постановка задачи применительно для КУП "СПЕЦКОММУНТРАНС": двум погрузчикам разной мощности, это автомобили ТО 28 и ТО 49, за 23 часа нужно погрузить на...
-
Рисунок 1 Устройство новой технологической платформы Устройство новой технологической платформы в образовании представлено на Рисунке 1. Ее ключевыми...
-
Решение., Оценка параметров уравнения регрессии - Корреляционно-регрессионный анализ
В нашем примере N=5 . Заполняем таблицу для удобства вычисления сумм, которые входят в формулы искомых коэффициентов. I=1 I=2 I=3 I=4 I=5 Xi 0 1 2 4 5 12...
-
Метод наименьших квадратов - Корреляционно-регрессионный анализ
Для определения коэффициентов уравнения регрессии b применяют разные методы (графический, метод средних), однако наибольшее распространение получил метод...
-
Процесс экономико-математического моделирования - Экономико-математические методы
Этот процесс состоит из нескольких взаимосвязанных этапов. Разбиение на этапы и выделение на каждом этапе присущих ему процессов условно: на одном из...
-
Метод Монте-Карло используют для вычисления интегралов, в особенности многомерных, для решения систем алгебраических уравнений высокого порядка, для...
-
Для моделирования случайных событий и процессов используется метод статистического моделирования. Сущность метода статистического моделирования. Таким...
-
Оценка адекватности моделей методом факторно-плоскостного пространственного проецирования
Оценка адекватности моделей методом факторно-плоскостного пространственного проецирования Современная автомобильная промышленность ставит перед...
-
Регрессия -- зависимость среднего значения какой-либо величины от некоторой другой величины или от нескольких величин. Задача регрессионного анализа...
-
Построение модели парной регрессии заключается в нахождении уравнения связи двух показателей x и y, то есть определяет, как изменение одного показателя...
-
Технологическое оформление процесса получения винилхлорида сбалансированным по хлору методом Первой стадией этого комбинированного процесса является...
-
Методы Кластерного Анализа, Иерархические методы - Кластерный анализ
Иерархические методы С понятием кластеризации мы познакомились в первом разделе курса. В этом мы опишем понятие "кластер" с математической точки зрения,...
-
Математическое ожидание, дисперсия Дискретной называют случайную величину, которая принимает отдельные, изолированные возможные значения с определенными...
-
Hysys - это интегрированная система, позволяющая рассчитывать как стационарные, так и динамические режимы работы, причем для моделирования стационарного...
-
Термодинамика процесса В процессах парофазного каталитического окисления моноатомных спиртов и этиленгликоля возможна реализация следующих превращений...
-
Данные для расчета: Основная реакция: (1) Побочные реакции: Рабочий объем катализатора - 24 м3. Расход оксида углерода и метанола на побочные продукты с...
-
Данную дипломную работу можно рассматривать как научно - исследовательскую работу (НИР). Работа является разработкой технологической схемы парофазного...
-
Выводы - Анализ способов получения глиоксаля и технологических схем окисления одноатомных спиртов
В ходе изучения процессов окисления спиртов были смоделированы в программной системе Hysys две технологические схемы производства формальдегида: - на...
Информационная оценка технологического совершенства сложных иерархических схем - Методы информационного анализа материальных процессов