Моделирование процесса теплопроводности - Компьютерное моделирование физических процессов и явлений, как метод научного познания
В качестве примера модели, в основе которой лежит уравнение матфизики, рассмотрим модель распространения тепла в однородном стрежне. Задача теплопроводности.
Процесс теплопроводности возникает, если тело неоднородно нагрето. Простейшая для изучения теплопроводности система - линейный однородный стержень. В простой модели боковая поверхность стержня считается теплоизолированной, т. е. через нее нет обмена теплом с окружающей средой.
Обозначим температуру стержня в точке с координатой х в момент времени t через u(x, t). Уравнение теплопроводности имеет вид
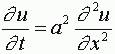
Где а - коэффициент температуропроводности, зависящий в первую очередь от вещества, из которого сделан стержень.
Уравнение теплопроводности сопровождается начальными и краевыми условиями, делающими постановку задачи физически однозначной Напомню, что если для дифуравнения заданы начальные условия (условия в начальный момент времени), то такая задача называется задачей Коши, если же заданы краевые условия (на границах исследуемой области), то такая задача называется краевой задачей, если заданы и начальные и граничные условия, то мы имеем смешанную краевую задачу. Начальное условие задает распределение температуры в стержне в начальный момент времени (считаем его равным нулю):
U(x,0) = ц(x)
Краевые условия (их должно быть в данном случае два) указывают, в простейшем варианте, какая температура поддерживается на концах стержня:
U(0,t)=ш0(t), u(l, t)=шl(t) (24)
Заметим, что начальные и граничные условия должны быть согласованы, т. е.
U(0,0) = ц(0)=ш0(0) (25)
U(l,0) = ц(l)=шl(0) (26)
Моделирование процесса теплопроводности связано с дискретизацией как временного изменения температуры, так и пространственного.
Введем равномерную прямоугольную сетку с помощью координатных линий
Xi=ih, i=0,1,....n (27)
Tj=jф, j=0,1,....m (28)
Где h - это шаг по пространству, по координате х, а ф - шаг по времени.
Значения функции в узлах сетки обозначим uij=u(xi, tj).
Получилась явная разностная схема, удобная в применении, но устойчивая лишь при выполнении условия
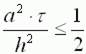
Это следует учитывать, выбирая шаги по времени и пространству.
Совокупность узлов в фиксированный момент времени называется слоем.
Построенная схема позволяет нам находить значение функции температур на j+1 слое через значения на j слое. Для начало счета при j=0 необходимо знать значения функции температур на нулевом слое. Они нам известны из начальных условий.
Если использовать другие конечно разностные соотношения для аппроксимации производных,
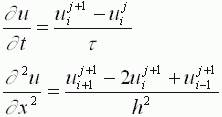
То получим существенно более устойчивую неявную схему
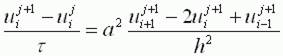
Или
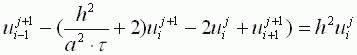
В отличие от явной схемы каждое разностное уравнение второй схемы содержит на каждом новом слое три неизвестные значения, которые невозможно определить сразу же, как мы поступали в явной схеме. При этом вторая разностная схема состоит из линейных трех точечных уравнений, т. е. каждое уравнение содержит неизвестную функцию в трех точках нового слоя. Такие системы линейных уравнений, системы с трехдиагональной матрицей, могут быть легко решены методом прогонки. Таким образом, в случае неявной схемы, чтобы посчитать значения функции температур в каждый следующий момент времени, т. е., чтобы перейти на следующий слой по времени, необходимо каждый раз решать методом прогонки линейную систему.
Похожие статьи
-
Тело бросают с высоты h под углом б к горизонту. Модель движения тела, брошенного под углом к горизонту строиться аналогично предыдущей модели, только...
-
Решение смешанной задачи для уравнения теплопроводности методом конечных разностей
Решение смешанной задачи для уравнения теплопроводности методом конечных разностей 1. Цель работы Ознакомление с методами решения смешанных задач для...
-
Использование современных информационно-коммуникационных технологий в образовательном учреждении позволяет решить ряд фундаментальных задач: Внедрить...
-
Существует два способа разработки компьютерных моделей с помощью специализированных программных средств и программирования. Специализированные...
-
Компьютерный моделирование информационный экспериментальный При физическом моделировании предполагается физическая однородность объекта и модели, их...
-
- наглядность построения; - обозримость основных свойств и отношений; - доступность ее для исследования или воспроизведения; - простота исследования,...
-
Для более сложных физических явлений, таких как процессы колебания, волновые процессы, процессы теплопроводности не всегда удается построить такие...
-
Различают типы уравнений в зависимости от соотношения между коэффициентами. 1) При a=b=c=f=0, d не 0, e не 0 получаем уравнение первого порядка вида...
-
Моделирование начинается с объекта изучения. На 1 этапе формируются законы, управляющие исследованием, происходит отделение информации от реального...
-
Примем, что тело массой m падает с высоты h с начальной скоростью V0. На тело действует сила тяжести F=mg, направленная вниз и сила сопротивления среды...
-
Физика - это наука, в которой математическое моделирование является весьма важным методом исследования. Исторически так сложилось, что моделирование...
-
Первый этап - определение целей моделирования. Основные из них таковы: 1. модель нужна для того, чтобы понять как устроен конкретный объект, какова его...
-
Вычислительный эксперимент - Компьютерное моделирование химико-технологических процессов
Увеличив в сотни миллионов раз скорость выполнения арифметических и логических операций и повысив тем самым производительность интеллектуального труда...
-
В зависимости от средств построения различают следующие классы моделей: Ь словесные или описательные модели их также называют вербальными или текстовыми...
-
Компьютерное моделирование, возникшее как одно из направлений математического моделирования с развитием информационных компьютерных технологий стало...
-
Начнем с того, что рассмотрим основные принципы моделирования, в сжатой форме отражающие тот достаточно богатый опыт, который накоплен к настоящему...
-
Компьютерное моделирование является одним из эффективных методов изучения физических систем. Часто компьютерные модели проще и удобнее исследовать, они...
-
Применение информационно-компьютерных технологий позволяет наиболее эффективно реализовать следующие функции урока: Вооружение учащихся глубокими и...
-
Окружающий человека мир действительно сложен и разнообразен. В процессе его познания человек вынужден выделять в исследуемых объектах наиболее важные...
-
В технологии компьютерного моделирования можно выделить следующие основные понятия. Модель - искусственно созданный объект, который воспроизводит в...
-
Введение - Компьютерное моделирование физических процессов и явлений, как метод научного познания
Важнейшей задачей преподавания физики, является формирование личности, способной ориентироваться в потоке информации в условиях непрерывного образования....
-
Метод Гомори последовательных отсечений - Математическое моделирование экономических процессов
При решении многих задач (планирование мелкосерийного производства, распределение кораблей по путям сообщения, выработка суждений типа "да-нет" и т. п.)...
-
Развитие методов многокритериальной оптимизации сложных систем обусловлено необходимостью повышения эффективности их функционирования на основе обобщения...
-
Понятие модель, моделирование. Разные взгляды и классификация Слова модель и моделирование в последние годы стали часто использоваться в учебной...
-
Моделирование как метод научного познания. - Моделирование перспективного развития экономики
Моделирование в научных исследованиях стало применяться еще в глубокой древности и постепенно захватывало все новые области научных знаний: техническое...
-
Компьютерный модель математический вычислительный 1. Сбор информации об объекте, выдвижение гипотез, предмодельный анализ; 2. Проектирование структуры и...
-
Процесс экономико-математического моделирования - Экономико-математические методы
Этот процесс состоит из нескольких взаимосвязанных этапов. Разбиение на этапы и выделение на каждом этапе присущих ему процессов условно: на одном из...
-
Частным случаем недетерминированной связи является связь случайная - стохастическая (вероятностная). Реализация вероятностного подхода к описанию...
-
Календарный производственный программирование однооперационный Все существующие методы решения задач календарного планирования3 по степени достижения...
-
В инженерной практике в настоящее время широко используются современные программные комплексы позволяющие моделировать сложные физические процессы. Для...
-
В экономической сфере деятельности в современных условиях большое значение имеет принятие решений. Для принятия экономических решений в нынешних условиях...
-
В 1974г. группа аргентинских ученых во главе с профессором А. Эррерой получила предварительные результаты работы над латиноамериканской моделью...
-
Пусть { , , ..., } - множество возможных состояний некоторой физической системы. В любой момент времени система может находиться только в одном...
-
Динамическое программирование - Математическое моделирование экономических процессов
В задачах линейного и нелинейного программирования экономический процесс считался статическим, т. е. не зависящим от времени, поэтому оптимальное решение...
-
Элементы матричного анализа - Методы решения системы линейных уравнений
Вектором, как на плоскости, так и в пространстве, называется направленный Отрезок , то есть такой Отрезок , один из концов которого выделен и называется...
-
Это раздел математического программирования, изучающий методы решения таких экстремальных задач, в которых результаты (эффективность) возрастают или...
-
Физическое моделирование - Основы научных исследований
Физическими моделированием называется изучение свойств явлений или процессов на физических моделях, заменяющих собою объект, который в таком случае...
-
- выполнять роль вспомогательного средства для решения задач, решаемых обычными вычислительными средствами, алгоритмами, технологиями; - выполнять роль...
-
К числу приближенных методов оптимизации задач календарного планирования относятся: частичный и направленный перебор, метод Монте-Карло,...
-
Равноускоренное (равнозамедленное) развитие. Этому типу динамики свойственно постоянное во времени увеличение (замедление) развития. Уровни таких рядов...
Моделирование процесса теплопроводности - Компьютерное моделирование физических процессов и явлений, как метод научного познания