Общетеоретические и методические концепции синергетического анализа сложных иерархических систем, Количество информации по Шеннону и Хартли. Связь между ними - Методы информационного анализа материальных процессов
Количество информации по Шеннону и Хартли. Связь между ними
Определение количества информации по Шеннону требует с самого начала привлечения теоретико-вероятностного подхода, в отличии от построения меры Хартли, где возможно ограничиться лишь понятиями комбинаторики. Это связано с тем, что исторически шенноновская теория информации выросла из потребностей теории связи, в которой приходится иметь дело со статистическими параметрами как передаваемых сообщений, так и каналов, по которым они передаются [22].
Таким образом, исходная постановка задачи определения количества информации теперь будет выглядеть следующим образом.
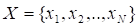
Пусть существует некоторое конечное множество событий, которые могут наступать с вероятностями соответственно, причем множество вероятностей удовлетворяет естественному условию нормировки
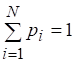
(2.1)
Исходное множество событий можно характеризовать присущей ему степенью неопределенности, или энтропией. В этом случае мощность исходного множества уже не будет единственным фактором, определяющим энтропию. Таким образом, степень неопределенности множества событий должна зависеть не только от их числа, но и от вероятностей, с которыми они наступают [23,24].
Прежде чем перейти к строгому обоснованию определения шенноновской энтропии, построим ее, воспользовавшись следующим приемом.
Пусть события исходного множества равновероятны: . Ясно, что для
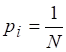
(2.2)
Энтропию исходного множества по Хартли можно переписать в виде суммы слагаемых
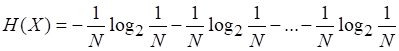
С учетом (2.2)
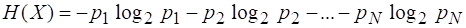
(2.3)
Предположим, что в случае множества, состоящего из неравновероятных событий, формула энтропии не изменится по сравнению с (2.3), тогда ее окончательно можно записать в виде
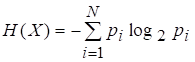
(2.4)
Пусть какое-либо событие множества реализуется, то есть становится достоверным и приобретает, следовательно, вероятность. Согласно (2.4) энтропия множества, состоящего из единственного достоверного события, есть
Если аналогично тому, как это делалось при построении хартлиевой меры информации, измерять количество информации, сообщаемое при наступлении определенного события из множества, изменением степени неопределенности, которая уменьшается до нуля, то шенноновское количество информации также численно совпадает с энтропией исходного множества:
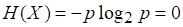
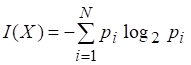
(2.5)
Как и в случае меры Хартли, в основу строгого вывода (2.4) необходимо положить определенную систему условий, которым должна удовлетворять мера Шеннона. Остановимся на системе условий, предложенной Шенноном, так как эта система наиболее наглядна и естественна в восприятии [1,25].
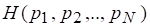
Для энтропии множества, содержащего событий, будем пользоваться обозначением.
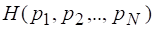
1. Функция должна быть непрерывной относительно всех своих аргументов. Этим обеспечивается отсутствие резких, скачкообразных изменений энтропии при малых изменениях вероятностей.
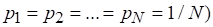
2. Если все событий множества равновероятны, то функция, где, должна монотонно возрастать с ростом. Это условие совпадает с одним из требований, предъявляемых к мере Хартли. Таким образом, степень неопределенности множества, состоящего лишь из равновероятных событий, может зависеть только от мощности множества, с ростом которой степень неопределенности, как и в случае меры Хартли должна монотонно возрастать.
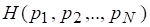
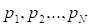
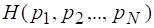
3. Значение функции не должно зависеть от порядка расстановки аргументов. Энтропия множества не изменяется при перестановке аргументов функции, так как энтропия должна определяться лишь мощностью множества и значениями вероятностей, с которыми наступают составляющие его события.
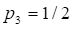
Прежде чем сформулировать последнее четвертое условие, приведем некоторые предварительные соображения. Воспользуемся примером, который в свое время рассмотрел Шеннон. Пусть имеется множество из трех событий, которые наступают с вероятностью соответственно, ,. Возможные пути реализации событий множества удобно представить в виде "дерева выборов 1", показанного на рисунке 1. Энтропия множества определяется значением функции
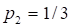
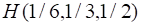
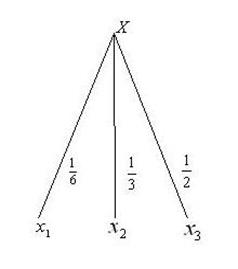
Рисунок 2 Дерево выборов 1
Разобьем множество на два подмножества. Первое подмножество пусть состоит из событий ; обозначим его. Второе подмножество составит единственное событие. Такому разбиению исходного множества соответствует "дерево выборов", изображенное на рисунке 3. Вероятность наступления нового события есть
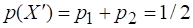
(2.6)
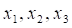
Числа, которыми помечены ветви дерева, ведущие из узла в узлы и, суть условные вероятности и. Нетрудно заметить, что в случае второго "дерева выборов" окончательные результаты для вероятностей наступления событий не изменились. Они определяются значениями:
Для события :
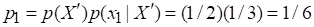
Для события :
Для события :
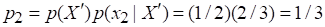
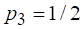
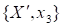
Предположим, что в этих условиях энтропии исходного множества и множества "с разбиением" одинаковы. Определим энтропию последнего из них. Степень неопределенности множества задается значением
.
Однако в случае реализации события неопределенность полностью не снимается - в соответствии с "деревом выборов 2" может наступить событие либо событие.
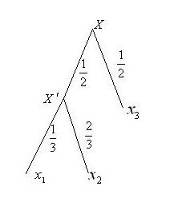
Рисунок 3 Дерево выборов 2
Степень неопределенности множества определяется как
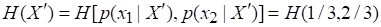
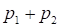
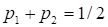
Но так как реализуется с вероятностью, то есть лишь в половине всех случаев, для нахождения энтропии множества "с разбиением" необходимо к степени неопределенности множества добавить степень неопределенности множества, умноженную на весовой коэффициент. Таким образом, с учетом замечания о равенстве энтропий исходного множества и множества "с разбиением" можно записать
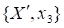
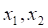
Преобразуем это равенство так, чтобы в него входили только значения вероятностей, определенные для элементов исходного множества. Условные вероятности события можно представить соответственно как
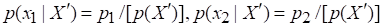
Или с учетом (2.6)
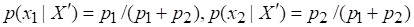
Тогда условие равенства энтропий окончательно запишется в виде
.
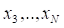
В данном примере исходное множество содержало три события. Видно, что аналогичные рассуждения можно провести применительно к множеству из элементов, если разбить его на подмножества и. Результат этих рассуждений сформулируем в виде условия 4.
4. Если в результате разбиения исходного множества на подмножества реализация событий производится в два последовательных этапа, то первоначальная энтропия должна быть взвешенной суммой индивидуальных энтропий этапов:
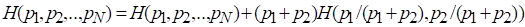
(2.7)
Теперь перейдем к доказательству того, что существует единственная функция, удовлетворяющая четырем перечисленным условиям, причем эта функция имеет вид (2.4).
Доказательство, следуя Шеннону, начнем с обобщения равенства (2.7), содержащегося в условии (4). Покажем, что
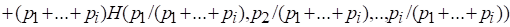
(2.8)
Для этого воспользуемся принципом математической индукции. При (2.8) сводится к (2.7), то есть выполняется. Допустим, что для некоторого (2.8) справедливо. Докажем, что это равенство выполняется для.
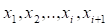
Разобьем множество событий на подмножества таким образом, что в первое подмножество войдут события. Тогда из условия 4 имеем
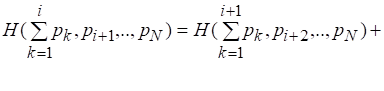
(2.9)
Кроме того, используя предположение о справедливости (2.8) для, запишем:
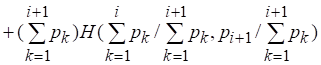
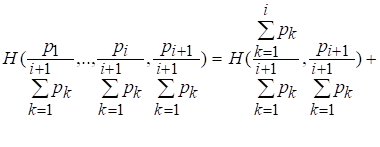
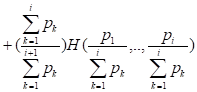
После умножения левой и правой частей последнего равенства на получим
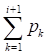
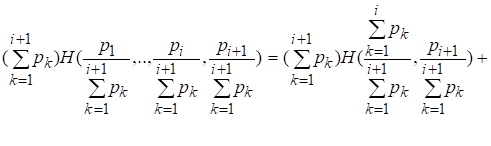
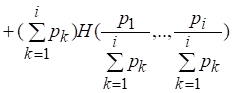
[26]. (2.10)
Перепишем формулу для, заменив первое слагаемое первой части (2.8) правой частью (2.9):
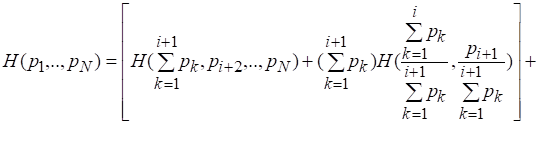
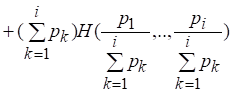
С учетом (2.10) получаем
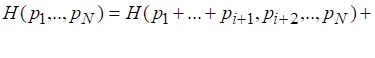
,
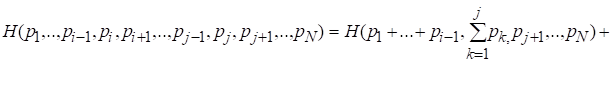
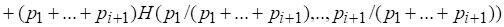
Что доказывает справедливость (2.8) для значения, а, следовательно, для любого.
Согласно условию 3 значение функции не должно зависеть от порядка расстановки ее аргументов, что позволяет следующим образом преобразовать (2.8):
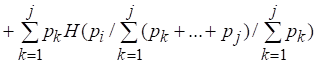
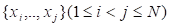
Здесь при реализации событий в два этапа из исходного множества выделяется подмножество элементов.
Последнее равенство можно обобщить на тот случай, когда исходное множество разбивается на подмножества событий
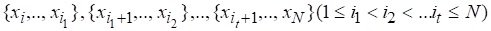
Равенство примет вид
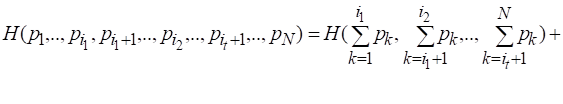
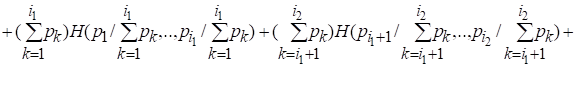
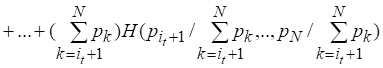
(2.11)
Равенство (2.11) представляет собой общую форму условия 4.
Обозначим. Это означает, что энтропию множества, содержащего лишь равновероятные события, можно рассматривать как функцию одного переменного. Допустим также, что, где и - целые числа, и что подмножества событий, вероятности наступления которых входят в равенство (2.11) имеют одинаковую мощность. Таких подмножеств будет, причем для их вероятностей будут выполняться равенства
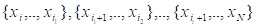
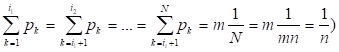
[27,28]. (2.12)
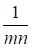
Каждый из аргументов функций, входящих в правую часть (2.11), начиная со второго слагаемого, с учетом (2.12) и того, что каждая вероятность равна, можно записать в виде
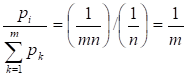
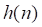
Таким образом, левую часть (2.11) можно представить как, первое слагаемое правой части - как, каждое слагаемое правой части, начиная со второго - как, причем этих слагаемых, как и подмножеств событий, имеется. Следовательно, при рассматриваемом разбиении исходного множества на равномощные группы событий равенство (2.11) приводится к виду
(2.13)
Покажем, что для функции справедливо равенство
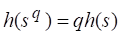
, (2.14)
Где и - целые числа.
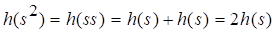
Для этого снова воспользуемся методом математической индукции. При (2.14) выполняется: , что непосредственно следует из (2.13). Допустим выполнение (2.14) для некоторого значения.
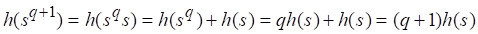
С (2.13) , то есть (2.14) выполняется для значения, а значит и для любого.
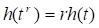
Перепишем (2.14) для новых аргументов: . Будем считать, что здесь и также целые числа, причем в (2.14) выберем таким, чтобы оно удовлетворяло условию
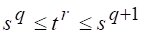
(2.15)
Прологарифмируем последнее неравенство: и разделим, на, что дает
(2.16)
Согласно условию 2, требующему монотонности функции, и с учетом (2.15) получим, или в силу (14) . После деления на получаем
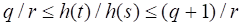
(2.17)
Из (2.16) и (2.17) видно, что величины и одинаково ограничены сверху и снизу. При достаточно большом эти отношения будут близки по значению, а так как ничто не мешает взять произвольно большим, можно сделать вывод о том, что
(2.18)
Зафиксируем, например, значение и обозначим. Тогда формула (2.18) примет вид
(2.19)
Так как логарифм возрастающая функция, а функция, согласно условию 2, должна быть возрастающей, можно прийти к выводу о положительности коэффициента.
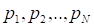
Теперь откажемся от сделанного ранее допущения о равновероятности событий множества, а именно предположим, что вероятности - это дроби вида
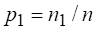
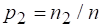
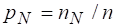
, ,..,, (2.20)
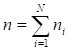
Где - целые числа. Если принять, то окажется что: ,
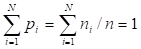
- рациональные числа. И для вероятностей выполняется необходимое условие нормировки (1), так как.
Рассмотрим новое множество, состоящее из равновероятных событий. Вероятность наступления любого события этого множества есть, а его энтропия
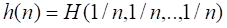
[29]. (2.21)
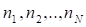
Произведем разбиение множества из элементов на подмножеств, содержащих соответственно элементов. Тогда согласно равенству (2.11)
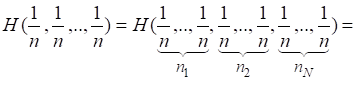
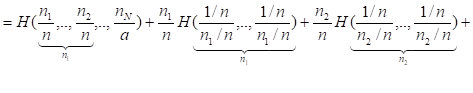
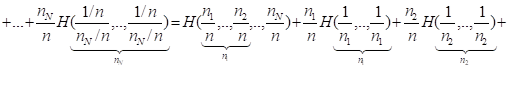
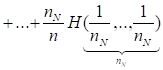
Отсюда, с учетом (2.20) и (2.21) получаем
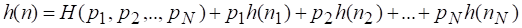
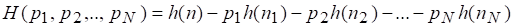
Используя условие нормировки (1), заменим множитель 2.1 перед первым слагаемым правой части последнего равенства на сумму вероятностей:
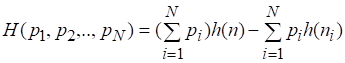
.
Перегруппировка слагаемых правой части дает
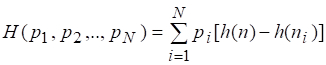
Согласно (2.18) и (2.20)
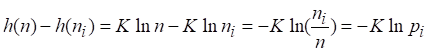
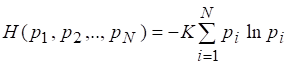
(2.22)
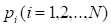
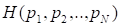
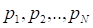
Ранее было принято допущение о том, что рациональные дроби. Однако условие 1, требующее непрерывности функции относительно своих аргументов, позволяет обобщить (2.22) и на случай иррациональных значений вероятностей. Это означает, что (2.22) справедливо для произвольных дробей. На этом вывод формулы (2.4) завершен, хотя она и отличается от (2.22) отсутствием коэффициента и основанием логарифмов. Также, как и в случае меры Хартли, выбор коэффициента определяет единицу энтропии. Если принять, то (2.22) полностью сведется к (2.4), а единицей энтропии и количества информации будет по-прежнему служить бит. Действительно, если множество состоит из двух равновероятных событий, то из (2.4) имеем
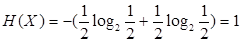
бит
В случае множества, содержащего равновероятных событий, (2.4) тривиально сводится к формуле энтропии, определяемой по Хартли, что видно из выкладок, предшествующих (2.4) и полностью согласуется с "физическим" смыслом второго условия, которому удовлетворяет мера Шеннона [11].
Похожие статьи
-
Рассмотрим основные идеи, лежащие в основе колмогоровского определения количества информации. Введение колмогоровской меры имеет основной целью уточнение...
-
Энтропия по Клаузиусу. Формулы Больцмана и Планка Во второй половине XX века произошли два события, которые в значительной мере определяют дальнейшие...
-
Анализировать общие механизмы энтропийно-информационных закономерностей материальных процессов, являющихся фундаментальной основой всех самопроизвольно...
-
Построим теперь на базе полиинтервальной оценки такую теоретико-вероятностную модель представления экспертных знаний, которая сочетала бы в себе описание...
-
Детерминация по Седову, Сороко, Малышеву - Методы информационного анализа материальных процессов
Одной из важнейших работ, в которой дан анализ энтропийно-информационных характеристик различного вида систем, является монография Е. А. Седова "Эволюция...
-
Пусть Dl, r() соответственно левые (правые) границы интервалов I, отвечающих на криволинейной трапеции ОИО значениям 0< < 1. Тогда интересующая нас...
-
Введение - Методы информационного анализа материальных процессов
Обоснование необходимости проведения данной дипломной работы. Использование меры определенности и неопределенности информации позволяет анализировать...
-
Элементы матричного анализа - Методы решения системы линейных уравнений
Вектором, как на плоскости, так и в пространстве, называется направленный Отрезок , то есть такой Отрезок , один из концов которого выделен и называется...
-
Введение - Метод представления знаний в интеллектуальных системах поддержки экспертных решений
Во многих областях человеческой деятельности - науке, технике, бизнесе - широко распространены проблемные ситуации, которые могут быть описаны исходными...
-
Энтропия. Движущее начало химических процессов - Химическая термодинамика. Термохимия. Решение задач
Убедившись в полезности знания тепловых эффектов химических превращений, мы, тем не менее, не смогли ответить на вопрос: "Почему одни химические реакции...
-
Методы определения корреляционной связи - Корреляционно-регрессионный анализ
Корреляцию и регрессию принято рассматривать как совокупный процесс статистического исследования, поэтому их использование в статистике часто именуют...
-
Предварительная обработка исходного числового ряда направлена на решение следующих задач (всех или части из них): снизить влияние случайной составляющей...
-
Методы непараметрической статистики - Основы теории систем и системного анализа
Использование классических распределений случайных величин обычно называют "параметрической статистикой" - мы делаем предположение о том, что...
-
Наиболее ранним способом формализации экономико-математических и ТС является представление физических явлений с помощью систем дифференциальных...
-
Счетные и несчетные множества - Методы решения системы линейных уравнений
Пусть, например, А и В Ї некоторые множества. Тогда их возможные взаимоотношения можно рассмотреть в виде таблицы: Диаграмма Венна Диаграмма Венна...
-
Пусть необходимо подобрать оптимальные настройки для объекта с передаточной функцией (9). Степень затухания, к примеру, ш= 0.75. Ниже даются рекомендации...
-
О квази-клике. - Использование квази-клик для анализа графа рынка России
Квази-клика - представляет собой релаксацию строгого условия полноты клики, то есть допускается отсутствие некоторых ребер в искомом подграфе. На данный...
-
Табличное представление цен действий и состояний задачи имеет естественные ограничения по масштабируемости задачи на большую размерность. В дискретных...
-
Кластерный анализ - Кластерный анализ
Кластерный анализ -- способ группировки многомерных объектов, основанных на представлении результатов отдельных наблюдений точками подходящего...
-
Алгоритм Метрополиса - Метод Монте Карло в химическом моделировании
В случае сложных жидкостей практически невозможно точно рассчитать значение конфигурационной статистической суммы системы. Однако его можно оценить с...
-
Вариации коэффициентов целевой функции ЗЛП приводят к изменению направления вектора градиента. Так как при этом не затрагивается допустимое множество, то...
-
Как уже отмечалось социально-экономическое прогнозирование, как и любое прогнозирование вообще, может быть успешным лишь при некоторой стабильности...
-
Элементы 4 и 8 в исходной схеме соединены последовательно. Заменяем их квазиэлементом С. В исходной схеме элементы 12 и 13 образуют параллельное...
-
Введение, Методы экстраполяции - Формализованные методы прогнозирования
К формализованным методам относятся методы экстраполяции и методы моделирования. Они базируются на математической теории. Среди методов экстраполяции...
-
В качестве меры априорной неопределенности системы (или прерывной случайной величины Х) в теории информации применяется специальная характеристика,...
-
Следствия теоремы, Послесловие к доказательству - Об одной теореме теории чисел
Не существует ЦЕЛЫХ чисел, для которых выполняется равенство (1). При четных значениях показателя степени уравнение вида (1) идентично как для...
-
В общем случае все этапы кластерного анализа взаимосвязаны, и решения, принятые на одном из них, определяют действия на последующих этапах. Аналитику...
-
Методы Кластерного Анализа, Иерархические методы - Кластерный анализ
Иерархические методы С понятием кластеризации мы познакомились в первом разделе курса. В этом мы опишем понятие "кластер" с математической точки зрения,...
-
Первый этап - определение целей моделирования. Основные из них таковы: 1. модель нужна для того, чтобы понять как устроен конкретный объект, какова его...
-
Компьютерное моделирование по сравнению с натурным экспериментом дает возможность: § получать наглядные динамические иллюстрации физических экспериментов...
-
Метод Гомори последовательных отсечений - Математическое моделирование экономических процессов
При решении многих задач (планирование мелкосерийного производства, распределение кораблей по путям сообщения, выработка суждений типа "да-нет" и т. п.)...
-
Взаимосвязи случайных событий - Основы теории систем и системного анализа
Вернемся теперь к вопросу о случайных событиях. Здесь методически удобнее рассматривать вначале простые события (может произойти или не произойти)....
-
Для моделирования случайных событий и процессов используется метод статистического моделирования. Сущность метода статистического моделирования. Таким...
-
Собственно-корреляционные параметрические методы изучения связи - Основы эконометрики
Измерение тесноты и направления связи является важной задачей изучения и количественного измерения взаимосвязи социально-экономических явлений. Оценка...
-
Численный сравнительный анализ - Ранговый метод оценивания параметров регрессионной модели
Итак, в рамках данной работы рассматриваются такие распределения случайных величин, как распределения Гаусса и Лапласа, треугольное распределение...
-
Метод наименьших квадратов - Корреляционно-регрессионный анализ
Для определения коэффициентов уравнения регрессии b применяют разные методы (графический, метод средних), однако наибольшее распространение получил метод...
-
Определение количества кластеров - Кластерный анализ
Существует проблема определения числа кластеров. Иногда можно априорно определить это число. Однако в большинстве случаев число кластеров определяется в...
-
Принципы декомпозиционного анализа экономической системы
Принципы декомпозиции Декомпозиция исходной системы или глобальной задачи производится путем применения принципов декомпозиции и координации. Первые...
-
Метод наименьших квадратов - Анализ методов прогнозирования
Расчет параметров af b для конкретной функциональной зависимости осуществляется с помощью метода наименьших квадратов (МНК) и его модификаций. Суть МНК...
-
В качестве примера модели, в основе которой лежит уравнение матфизики, рассмотрим модель распространения тепла в однородном стрежне. Задача...
Общетеоретические и методические концепции синергетического анализа сложных иерархических систем, Количество информации по Шеннону и Хартли. Связь между ними - Методы информационного анализа материальных процессов