Обзор существующих методов исчисления количества информации и энтропии, Энтропия по Клаузиусу. Формулы Больцмана и Планка - Методы информационного анализа материальных процессов
Энтропия по Клаузиусу. Формулы Больцмана и Планка
Во второй половине XX века произошли два события, которые в значительной мере определяют дальнейшие пути развития науки, научного постижения мира, теоретического и практического совершенства любых объектов. Речь идет о создании теории информации, установлении свойств информационных мер и о начале анализа механизмов энтропийно-информационных закономерностей, для изучения которых синергетика привлекает все новейшие достижения неравновесной термодинамики, теории информации и общей теории систем. Стремление к детерминированному описанию реальных процессов неизбежно приводит к субъективному или объективному идеализму и тем самым вносит в процесс и результат познания - стохастичность, связанную с различием точек зрения, трактовок и версий разных авторов. Возникновение теории информации тесно связано с именем К. Шеннона, предложившего решение основной проблемы о нахождении скорости передачи информации, которую можно достичь при оптимальном методе кодирования и декодирования так, чтобы вероятность ошибки при передаче информации была как угодно мала. Теорию кодирования отличает то, что наряду со статистическими методами она использует для построения конкретных кодов глубокие алгебраические и комбинаторные идеи. Активно разрабатываются теория семантической информации, которая решает проблемы количественной оценки информации с учетом ее смысла, теория прагматической информации с учетом ее ценности [4].
Слово "энтропия" было впервые использовано в 1864г. Рудольфом Клаузиусом для названия величины, характеризующей процессы перехода тепловой энергии в механическую, и в термодинамике оно сохранило именно это значение. В своем главном научном труде, трехтомной монографии "Механическая теория тепла", Рудольф Клаузиус подробно объясняет целесообразность введения этого совершенно особого нового понятия ссылкой на выполнение при так называемых обратимых круговых процессах следующего уравнения:
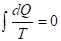
, (1.1)
Где - элементарное количество теплоты; - абсолютная температура.

Под энергией понимается общая мера различных процессов и видов взаимодействия. Для выяснения физического содержания этого понятия рассматривают отношение теплоты, полученной телом в изотермическом процессе, к температуре теплоотдающего тела, называемое приведенным количеством теплоты. Приведенное количество теплоты, сообщаемое телу на бесконечно малом участке процесса, равно. На основании теоретического анализа установлено, что приведенное количество теплоты, сообщаемое телу в любом обратимом круговом процессе, равно нулю. Из равенства нулю интеграла (1.1), следует, что подынтегральное выражение есть полный дифференциал некоторой функции, которая определяется только состоянием системы и не зависит от пути интегрирования. Таким образом:

. (1.2)
Проинтегрируем обе части равенства (1.2):

, (1.3)
Где - элементарное количество теплоты; - абсолютная температура; - энтропия.
Уравнение (1.3) дает еще одно выражение второго начала механической теории теплоты, очень удобное во многих исследованиях [5,6].
Предложенная Клаузиусом формула энтропии (1.3) не раскрывала внутренних механизмов процессов, приводящих к возрастанию энтропии. Данная проблема была решена Л. Больцманом (1872г.), предложившим формулу, связывающую энтропию с логарифмом вероятности состояний системы:
, (1.4)
Где - постоянная Больцмана; - математическая энтропия.
Согласно Больцману, величина определяется:

(1.5)
Где - общее число молекул газа; - число молекул, движущихся со скоростями, соответствующими I-ой ячейке, .
Данное условие означает, что все молекул распределены по соответствующим ячейкам пространства скоростей, в количествах, учитываемых уравнением (1.5). Согласно (1.5), применяя свойства логарифмической функции, заключаем, что перестановка молекул, находящихся внутри каждой из ячеек, не влияет на величину . Отсюда следует, что рассчитанная по формуле (1.5) математическая энтропия соответствует числу возможных микросостояний системы, при котором макросостояние системы остается неизменным [7]. М. Планк преобразовал формулу Больцмана (1.5), применяя для этого асимптотическое представление Стирлинга:
. (1.6)
В результате подстановки (1.6) в (1.5) получается соотношение:

.

С учетом условия выражение для математической энтропии приводится к виду:

. (1.7)
Далее Планк ввел в рассмотрение вероятности различных состояний молекул, определив их по формуле:

, (1.8)
Где и - соответственно доля и число частиц с энергией ; - общее число частиц; - число учитываемых энергетических уровней.
Используя формулу (1.8), второе слагаемое в правой части (1.7) можно представить в виде суммы:

. (1.9)

С учетом известного из теории вероятностей условия нормировки подстановка (1.9) в (1.7) приводит выражение для математической энтропии Больцмана к виду:


. (1.10)
Выражение (1.10) соответствует полной энтропии системы [8]. Поделив подсчитанную по формуле (1.10) величину на, можно определить усредненную величину энтропии, относящуюся к одному элементу рассматриваемой системы:

. (1.11)
Для перехода к физической энтропии математическая энтропия умножается на постоянную Больцмана и на число частиц :

. (1.12)
Постоянная Больцмана относится к одной частице размерностью. Отсюда следует, что математическая - энтропия Больцмана, не зависит от общего числа частиц, поскольку оно не фигурирует ни под знаком суммы, ни в пределах суммирования. Тогда перемножение величин и является некорректным, так как если подставить в (1.11) значение, получим:

.
Откуда из свойств логарифмической функции следует при.
Похожие статьи
-
Введение - Методы информационного анализа материальных процессов
Обоснование необходимости проведения данной дипломной работы. Использование меры определенности и неопределенности информации позволяет анализировать...
-
Второе начало термодинамики. Энтропия Из предыдущих глав мы знаем много обратимых процессов, но есть и необратимые, например: - переход тепла от горячего...
-
Первый этап - определение целей моделирования. Основные из них таковы: 1. модель нужна для того, чтобы понять как устроен конкретный объект, какова его...
-
Второе начало термодинамики. Энтропия Объединенное уравнение первого и второго начал термодинамики Рис. 12 Из выражения первого начала термодинамики U =...
-
Общая схема метода Монте-Карло Сущность метода Монте-Карло состоит в следующем: требуется найти значение а некоторой изучаемой величины. Для этого...
-
Энтропия. Самопроизвольный процесс - Химическая термодинамика и ее процессы
Самопроизвольный процесс - процесс, который может протекать без затраты работы извне, причем в результате может быть получена работа в количестве,...
-
Энтропия. Движущее начало химических процессов - Химическая термодинамика. Термохимия. Решение задач
Убедившись в полезности знания тепловых эффектов химических превращений, мы, тем не менее, не смогли ответить на вопрос: "Почему одни химические реакции...
-
Определение количества кластеров - Кластерный анализ
Существует проблема определения числа кластеров. Иногда можно априорно определить это число. Однако в большинстве случаев число кластеров определяется в...
-
Адсорбционные методы исследования свойств поверхности позволяют количественно охарактеризовать происходящие при адсорбции межмолекулярные взаимодействия,...
-
Рисунок 1 Устройство новой технологической платформы Устройство новой технологической платформы в образовании представлено на Рисунке 1. Ее ключевыми...
-
Элементы матричного анализа - Методы решения системы линейных уравнений
Вектором, как на плоскости, так и в пространстве, называется направленный Отрезок , то есть такой Отрезок , один из концов которого выделен и называется...
-
В технологии компьютерного моделирования можно выделить следующие основные понятия. Модель - искусственно созданный объект, который воспроизводит в...
-
В термодинамике понятие "энтропия" было введено Р. Клаузиусом (1865), который показал, что процесс превращения теплоты в работу следует общей физической...
-
Успешная визуализация и имитирование реальной среды взаимодействия человека и техники посредством компьютера разработана Национальным аэрокосмическим...
-
ЕДИНИЦЫ КОЛИЧЕСТВА ИНФОРМАЦИИ: ВЕРОЯТНОСТНЫЙ И ОБЪЕМНЫЙ ПОДХОДЫ - Информация, ее виды и свойства
Определить понятие "количество информации" довольно сложно. В решении этой проблемы существуют два основных подхода. Исторически они возникли почти...
-
Уровень науки и техники Надежность средств, с помощью которых человек достигает космоса высокая, но не идеальна. РН -- сложная конструкция, и даже в...
-
Для моделирования случайных событий и процессов используется метод статистического моделирования. Сущность метода статистического моделирования. Таким...
-
Итеративные методы, Алгоритм k-средних (k-means) - Кластерный анализ
При большом количестве наблюдений иерархические методы кластерного анализа не пригодны. В таких случаях используют неиерархические методы, основанные на...
-
Начнем с того, что рассмотрим основные принципы моделирования, в сжатой форме отражающие тот достаточно богатый опыт, который накоплен к настоящему...
-
Поляризация электрода - Электрохимические методы анализа
Если к системе электродов, погруженных в раствор, приложить напряжение, то по цепи будет проходить электрический ток. При этом на электродах будут...
-
Операционно-техническое разделение труда в процессе управления - Управление операциями с информацией
Операционно-техническое разделение труда в процессе управления обусловлено его динамикой. Процесс управления в динамике можно представить с помощью...
-
ЗАКЛЮЧЕНИЕ - Практические аспекты эконометрического анализа
Эконометрика - это наука, которая изучает статистические закономерности в экономике. Объектом изучения эконометрики, как самостоятельного раздела...
-
МЕТОДЫ ОСАЖДЕНИЯ, ИОННОГО ОБМЕНА, МЕМБРАННЫЕ МЕТОДЫ - Химические свойства и строение воды
Современные технологии позволяют изготавливать объемные или плоские фильтрующие материалы с однородными каналами практически любого размера. Мембранный...
-
Способы получения коллоидных систем - Общая характеристика дисперсных систем и методы их получения
Коллоидные системы по степени дисперсности занимают промежуточное положение между истинными растворами и грубодисперсными системами. Поэтому коллоидные...
-
В настоящее время нельзя назвать область человеческой деятельности, в которой в той или иной степени не использовались бы методы моделирования. Особенно...
-
При Расчете системы разделения данной технологической схемы, мы сталкиваемся с некоторыми сложностями. Дело в том, что предлагаемые термодинамические...
-
Модель в общем смысле (обобщенная модель) есть создаваемый с целью получения и (или) хранения информации специфический объект (в форме мысленного образа,...
-
Информация для моделирования - Математическое моделирование в лесной промышленности
Информация для моделирования носит разнообразный характер - детерминированная и случайная, нормативная и расчетная, достоверная и недостоверная,...
-
В основе моделирования лежит теория подобия, которая утверждает, что абсолютное подобие может иметь место лишь при замене одного объекта другим точно...
-
Наглядное - на базе представлений человека о реальных объектах создаются различные наглядные модели, отображающие явления и процессы, протекающие в...
-
С развитием системных исследований, с расширением экспериментальных методов изучения реальных явлений все большее значение приобретают абстрактные...
-
Для достижения поставленной цели предприятию требуются материалы, оборудование, энергия, рабочая сила и другие ресурсы. Каждое предприятие такими...
-
Общие теоретические положения метода Монте Карло Метод Монте Карло, применяемый в статистической физике, является частным случаем общего метода...
-
Теоретическое обоснование математического моделирования - Математические методы и модели в экономике
Коммерческая деятельность в том или ином виде сводится к решению таких задач: как распорядиться имеющимися ресурсами для достижения наибольшей выгоды или...
-
В общем случае все этапы кластерного анализа взаимосвязаны, и решения, принятые на одном из них, определяют действия на последующих этапах. Аналитику...
-
Химизм процесса гидроочистки - Сравнительный анализ методов обессеривания
Превращение серосодержащих соединений В неуглеводороных соединениях связи C-S и S-S менее прочны, чем связи С-С и С-Н, усредненные энергии связи которых...
-
Реагенты Продукты, Все химические реакции обратимы, Вопросы - Химическое равновесие
Все химические реакции обратимы Это означает, что в реакционной смеси протекает как взаимодействие реагентов, так и взаимодействие продуктов. В этом...
-
Классический подход - изучение взаимосвязей между отдельными частями, и разработка модели системы рассматривается как суммирование отдельных компонент в...
-
Обзор методов получения хлорпарафинов - Теоретические основы получения хлорпарафинов
Известен способ получения жидких хлорпарафинов в промышленном масштабе хлорированием парафина в расплаве. Процесс состоит из следующих стадий: 1....
-
Заключение - Анализ методов прогнозирования
На основании проведенного исследования можно сделать следующие выводы и предложения: 1. Под прогнозом понимается система научно обоснованных...
Обзор существующих методов исчисления количества информации и энтропии, Энтропия по Клаузиусу. Формулы Больцмана и Планка - Методы информационного анализа материальных процессов