Примеры экономических задач, приводящихся к задачам ЛП - Решение оптимизационных экономических задач методами линейного программирования
Несмотря на требование линейности функций критериев и ограничений, в рамки линейного программирования попадают многочисленные задачи распределения ресурсов, управления запасами, сетевого и календарного планирования, транспортные задачи и прочие.
Рассмотрим некоторые из них.
Определение оптимального ассортимента. Имеются m видов ресурсов в количествах b1, b2,., bI, bM и n видов изделий. Задана матрица A=||aIj||, i=1,.,m, j=1,.,n, где aIj характеризует нормы расхода i-го ресурса на единицу j-го вида изделий. Эффективность производства j-го вида изделий характеризуется показателем CJ, удовлетворяющим условию линейности. Нужно определить такой план выпуска изделий (оптимальный ассортимент), при котором суммарный показатель эффективности будет наибольший.
Обозначим количество единиц k-го вида изделий, выпускаемых предприятием, через xK, . Тогда математическая модель этой задачи будет иметь такой вид:

(3.1)
При ограничениях
(3.2)
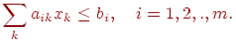
Кроме ограничений на ресурсы (3.2) в эту модель можно ввести дополнительные ограничения на планируемый уровень выпуска продукции, xI: xJ: xK = bI: bJ: bK для всех i, j, k и т. д.
Оптимальное распределение взаимозаменяемых ресурсов. Имеются m видов взаимозаменяемых ресурсов а1, а2,., аM, используемых при выполнении n различных работ (задач). Объемы работ, которые должны быть выполнены, составляют b1, b2,., bI, bN единиц. Заданы числа, указывающие, сколько единиц j-й работы можно получить из единицы і-го ресурса, а также CIj - затраты на производство j-й работы из единицы i-го ресурса.
Требуется распределить ресурсы по работам таким образом, чтобы суммарная эффективность выполненных работ была максимальной (или суммарные затраты - минимальными).
Данная задача называется общей распределительной задачей. Количество единиц i-го ресурса, которое выделено на выполнение работ j-го вида, обозначим через xIj.
Математическая модель рассматриваемой задачи такова:
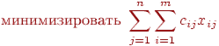
(3.3)
При ограничениях
(3.4)
(3.5)

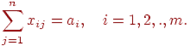
Ограничение (3.4) означает, что план всех работ должен быть выполнен полностью, а (3.5) означает, что ресурсы должны быть израсходованы целиком.
Примером этой задачи может быть задача о распределении самолетов по авиалиниям.
Задача о смесях. Имеется р компонентов, при сочетании которых в разных пропорциях получают разные смеси. Каждый компонент, а следовательно и смесь, содержит q веществ. Количество k-го вещества k = 1, 2,., q, входящее в состав единицы і-го компонента и в состав единицы смеси, обозначим через аIk и аK соответственно.
Предположим, что аK зависит от аIk линейно, то есть если смесь состоит из x1 единиц первого компонента, x2 - единицу второго компонента и т. д., то
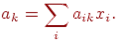
Задано р величин CI, характеризующих стоимость, массу или калорийность единицы i-го компонента, и q величин bK, указывающих минимально необходимое процентное содержание k-го вещества в смеси. Обозначим через x1, x2,.,xР значение компонента р-го вида, входящего в состав смеси.
Математическая модель этой задачи имеет такой вид:
(3.6)

При ограничении
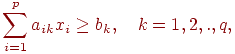
(3.7)
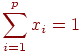
Ограничение (3.7) означает, что процентное содержание k-го вещества в единице смеси должно быть не меньше bK.
К этой же модели принадлежит также задача определения оптимального рациона кормления скота.
Похожие статьи
-
Экономико-математические методы и моделирование в землеустройстве позволяют решать большой круг задач, связанных с оптимизацией территориальной...
-
Линейное программирование в экономике - Экономико-математические методы
Задача о наилучшем использовании ресурсов. Пусть некоторая производственная единица (цех, завод, фирма и т. д.), исходя из конъюнктуры рынка, технических...
-
Линейное программирование, Общая задача линейного программирования - Экономико-математические методы
Термин "линейное программирование" впервые появился в 1951 г. в работах американских ученых (Дж. Данциг, Т. Купманс), а первые исследования по линейному...
-
Модели линейного программирования. Основные определения Еще одним классом задач экономико-математического моделирования являются задачи линейного...
-
Исходная задача: При ограничениях: Двойственной является следующая задача: При ограничениях: Число неизвестных в двойственной задаче равно 2....
-
В разделе 1 курсовой работы требуется: Определить количество закупаемого заданным филиалом фирмы сырья у каждого АО, (xj), максимизируя прибыль филиала....
-
Введение - Решение оптимизационных экономических задач методами линейного программирования
Линейное программирование является составной частью раздела математики, который изучает методы нахождения условного экстремума функции многих переменных...
-
Для достижения поставленной цели предприятию требуются материалы, оборудование, энергия, рабочая сила и другие ресурсы. Каждое предприятие такими...
-
При решении экономических задач часто анализировать ситуации, в которых сталкиваются интересы двух или более конкурирующих сторон, преследующих различные...
-
Динамическое программирование Динамическое программирование -- один из разделов оптимального программирования, в котором процесс принятия решения и...
-
Необходимость введения нового ограничения может возникнуть, например, когда первоначально для сокращения затрат машинного времени некоторые интуитивно...
-
Ограничение чувствительность задача программирование Вариации правых частей ограничений приводят к изменению области допустимых решений ЗЛП, в действии...
-
ОБЩАЯ ПОСТАНОВКА ЗАДАЧИ ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ (ЗЛП) - Линейное программирование в экономике
Линейное программирование - направление математики, изучающее методы решения экстремальных задач, которые характеризуются линейной зависимостью между...
-
Как известно решение задач симплексным методом применяется очень часто. Это связано с тем, что симплексный метод подходит для решения широкого круга...
-
Решим прямую задачу линейного программирования симплексным методом, с использованием симплексной таблицы. Определим максимальное значение целевой...
-
Математическая модель транспортной задачи: F = ??cIjXIj, (1) При условиях: ?xIj = aI, i = 1,2,..., m, (2) ?xIj = bJ, j = 1,2,..., n, (3)...
-
Необходимо найти минимальное значение целевой функции F = 4x1+18x2 > min, при системе ограничений: X1+4x2?14(1) X1+6x2?15(2) X1+x2?5(3)...
-
Задачей линейного программирования (ЛП) называется задача минимизации или максимизации линейного функционала при линейных ограничениях. В литературе...
-
Это раздел математического программирования, изучающий методы решения таких экстремальных задач, в которых результаты (эффективность) возрастают или...
-
Задача о загрузке рюкзака (задача о ранце) - Метод динамического программирования для решения задач
Постановка задачи. Пусть имеются N видов грузов с номерами. Единица груза j-го вида имеет все aJ. Если груз j-го вида берется в количестве xJ, то его...
-
Вариации коэффициентов целевой функции ЗЛП приводят к изменению направления вектора градиента. Так как при этом не затрагивается допустимое множество, то...
-
Так как целевая функция не является линейной, то эта задача является задачей нелинейного программирования. Найдем ее решение, используя геометрическую...
-
Большое число экономических и планово-производственных задач связано с распределением каких-либо, как правило, ограниченных ресурсов (сырья, рабочей...
-
Известно оптимальное решение X*=(0;0;1;1) задачи линейного программирования: Составьте двойственную задачу и найдите ее оптимальное решение по теореме...
-
Основные понятия теории экономико-математического моделирования Кибернетический подход к исследованию экономико-математических систем Обычно...
-
Изучение теоретических вопросов анализа чувствительности оптимального решения ЗЛП к вариациям некоторых параметров задачи и введению нового ограничения....
-
Тема, с которой мы сегодня ознакомимся это "Применение матриц при решении экономических задач." Рассмотрим как с помощью матриц можно решать...
-
Критерии оптимальности в задачах с ограничениями - Линейное программирование в экономике
Ряд инженерных задач связан с оптимизацией при наличии некоторого количества ограничений на управляемые переменные. Такие ограничения существенно...
-
Во многих экономических моделях исследования операций зависимости между постоянными и переменными факторами лишь в первом приближении можно считать...
-
Второй раздел курсовой работы посвящен особенностям постановки и решения общей задачи линейного программирования, а именно, транспортной задаче (ТЗЛП)....
-
Литература - Решение оптимизационных экономических задач методами линейного программирования
1. Карпелович Ф. И., Садовский Л. Е. Элементы линейной алгебры и линейного программирования. - М.: Физматгиз, 1963. 2. Коротков М., Гаврилов М. "Основы...
-
Иногда необходимо управлять сложными комплексами взаимосвязанных работ, направленных на достижение определенных целей. Примерами таких комплексов в...
-
В начале пятилетнего периода работы предприятию выделена сумма в C руб. для приобретения нового оборудования. Стоимость одного комплекта оборудования...
-
Математическая модель задачи нелинейного программирования (ЗНП) (*) Для ЗНП в отличие от Задачи Линейного Программирования (ЗЛП) нет единого метода...
-
Системы массового обслуживания -- это такие системы, в которые в случайные моменты времени поступают заявки на обслуживание, при этом поступившие заявки...
-
Пусть имеется оптимизационная задача вида: (1) (2) (3) - задан(4) Здесь предполагается, что FJ(xJ,yJ)>0 для всех допустимых значений xJ,yJ. В этом случае...
-
Пример транспортной задачи линейного программирования - Оптимальное программирование
Транспортная задача -- математическая задача линейного программирования специального вида о поиске оптимального распределения однородных объектов из...
-
Наша группа работала над учебным межпредметным проектом "Математические модели в рыночной экономике". Мы покажем применение в экономике систем уравнений....
-
Параметрическое линейное программирование - Методы линейного программирования
Представляет собой один из разделов математического программирования, изучающий задачи, в которых целевая функция или ограничения зависят от одного или...
-
Календарный производственный программирование однооперационный Все существующие методы решения задач календарного планирования3 по степени достижения...
Примеры экономических задач, приводящихся к задачам ЛП - Решение оптимизационных экономических задач методами линейного программирования