Параметрическое линейное программирование - Методы линейного программирования
Представляет собой один из разделов математического программирования, изучающий задачи, в которых целевая функция или ограничения зависят от одного или нескольких параметров.
С математической точки зрения параметрическое программирование выступает как одно из средств анализа чувствительности решения к вариации исходных данных, оценки устойчивости решения.
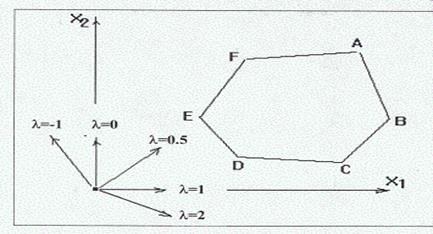
Если обратиться к геометрической интерпретации задачи, то можно заметить, что вектор-градиент линейной формы определяется ее параметром. Например, для целевой функции L(X, л) = лX1 + (1-л)X2 при различных значениях параметра л градиент определяет различные направления роста функции.
Нетрудно видеть, что, если при некотором значении параметра максимум достигается в вершине A, то небольшая вариация этого значения несколько изменит направление градиента, но не изменит положение точки максимума. Отсюда, что некоторый оптимальный при л = л0 оптимален и в окрестности л0, т. е. при б ? л ? в где л0 [б, в].
Считая значение параметра равным некоторому числу, находим оптимальный план Х* или устанавливаем неразрешимость полученной задачи линейного программирования.
Определяют множество значений параметра, для которых найденный оптимальный план является оптимальным или задача неразрешима. Эти значения параметра исключаются из рассмотрения.
Полагают значение параметра равным некоторому числу, принадлежавшему оставшейся части промежутка, и находят решение полученной задачи линейного программирования.
Определяют множество значений параметра, для которых новый оптимальный план остается оптимальным или задача неразрешима. Вычисления повторяются до тех пор, пока не будут исследованы все значения параметра.
Предприятие должно выпустить два вида продукции А и В, для изготовления которых используется три вида сырья, нормы расходов заданы в таблице. Известно, что цена на А единицу продукции может изменяться от 2 до 12 у. е., для В от 13 до 3 у. е. Найти оптимальные планы выпуска для заданных интервалов цен.
|
А |
В |
ЗАПАСЫ | |
|
1 |
4 |
1 |
16 |
|
2 |
2 |
2 |
22 |
|
3 |
6 |
3 |
36 |
Обозначим через Х1 количество единиц продукции А, через X2 -- количество единиц продукции В. Математическая модель задачи имеет вид
При ограничениях:
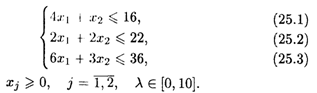
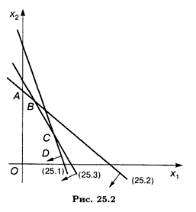
Область допустимых решений -- многоугольник OABCD (рис. 25.2). Полагая л = 0, L() = 2X1 + 13Х2 строим (2, 13). Перемещая линию уровня по направлению, находим, что в точке А(0, 11) задача имеет оптимальное решение. Таким образом, при л = 0 1опт(0, 11), L(1)Max = 143.
Если уравнение прямой имеет вид
При ограничениях
Область допустимых решений -- многоугольник OABCD (рис. 25.2). Полагая л = 0, L(Х) = 2X1 + 13Х2 строим (2, 13). Перемещая линию уровня по направлению С, находим, что в точке А(0, 11) задача имеет оптимальное решение. Таким образом, при л = 0 х 1опт(0, 11), L(1)Max = 143.
Если уравнение прямой имеет вид
То угловой коэффициент равен K = - А/В.
Угловой коэффициент линии уровня, перпендикулярной С, При произвольном значении л равен K = (2 + л) / (13 - л).
Найдем область оптимальности Х 1опт: Х 1опт будет оставаться оптимальным для всех л, при которых соответствующая линия уровня находится внутри угла, образованного прямыми X1 = 0 и (25.2). Угловой коэффициент прямой (25.2) K = - 2/2 = -1. По условию л1 = 0, л2 = (2 + л) / (13 - л) = -1, откуда л2 = 11/2. Решение Х 1опт остается оптимальным при л Э [0, 11/2].
При л = 11/2 линия уровня совпадает с прямой (25.2) и оптимальными будут все точки, лежащие на прямой (25.2), в том числе и точка В(1, 10), лежащая на пересечении прямых (25.2) и (25.3).
Оптимальное решение будет сохраняться до тех пор, пока при изменении л линия уровня не совпадет с прямой (25.3), что будет соответствовать новому оптимальному решению 2опт. Найдем новый диапазон изменения л: л1 = 11/2, л2 = (- 2 + л) / (13 - л) = -2, так как K3 = -2. Откуда л2 = 8.
Получили при л Э [11/2, 8] Х 2опт = (1, 10), L( х 2)Max = 132 - 9л.
Аналогично определяем, что при л Э [8,10], Х 3опт = (2, 8), L( Х 3)mах = 108 - 6л.
Таким образом, при л = [0, 11/2] необходимо производить только 11 изделий В, при этом стоимость продукции будет максимальной и равной (143 - 11л) усл. ед.; при л Э [11/2, 8] необходимо производить одно изделие А и 10 изделий В, при этом стоимость продукции является максимальной и равной (132 - 9л) усл. ед.; при л Э [8, 10] необходимо производить 2 изделия А и 8 изделий В, при этом стоимость продукции будет максимальной и равной (108 - 6л) усл. ед.
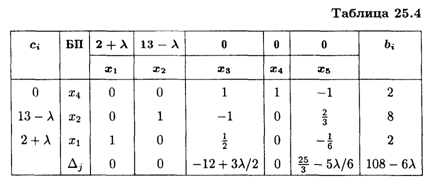
Найдем решение этой же задачи симплексным методом (табл. 25.2-25.4), для чего приведем задачу к каноническому виду:
При ограничениях:
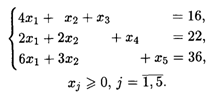
Получим л1 = -, так как все Д"J ? 0;
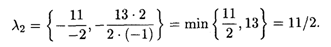
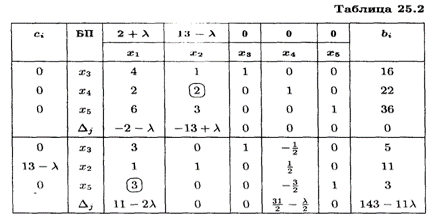
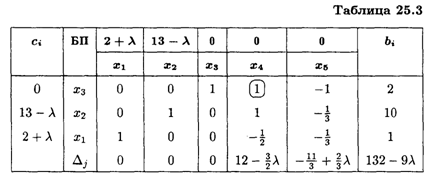
Таким образом, л э [0, 11/2], Х 1опт = (0, 11, 5, 0, 3), L( Х 1)max = 143 - 11л.
Получим:
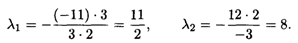
Таким образом, л Э [8, 10],Х 3опт = (2, 8, 0, 2, 0), L(Х 3)mах = 108 - 6л.
Получили следующие оптимальные решения в зависимости от диапазона изменения л:
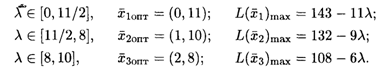
Список литературы
- 1. Волков С. И. Землеустройство. Экономико - математические методы и модели. 2002 год. 2. Кундиус. Математические методы в экономике и моделирование социально-экономических процессов в АПК. 2001 год. 3. Полунин. Математическое програмирование в землеустройстве. 1972 год.
Похожие статьи
-
Исходная задача: При ограничениях: Двойственной является следующая задача: При ограничениях: Число неизвестных в двойственной задаче равно 2....
-
В разделе 1 курсовой работы требуется: Определить количество закупаемого заданным филиалом фирмы сырья у каждого АО, (xj), максимизируя прибыль филиала....
-
Математическая модель задачи нелинейного программирования (ЗНП) (*) Для ЗНП в отличие от Задачи Линейного Программирования (ЗЛП) нет единого метода...
-
Это раздел математического программирования, изучающий методы решения таких экстремальных задач, в которых результаты (эффективность) возрастают или...
-
Ограничение чувствительность задача программирование Вариации правых частей ограничений приводят к изменению области допустимых решений ЗЛП, в действии...
-
Задача о загрузке рюкзака (задача о ранце) - Метод динамического программирования для решения задач
Постановка задачи. Пусть имеются N видов грузов с номерами. Единица груза j-го вида имеет все aJ. Если груз j-го вида берется в количестве xJ, то его...
-
Основные понятия линейного программирования - Оптимальное программирование
Математические исследования отдельных экономических проблем, математическая формализация числового материала проводилась еще в XIX веке. При...
-
Так как целевая функция не является линейной, то эта задача является задачей нелинейного программирования. Найдем ее решение, используя геометрическую...
-
Счетные и несчетные множества - Методы решения системы линейных уравнений
Пусть, например, А и В Ї некоторые множества. Тогда их возможные взаимоотношения можно рассмотреть в виде таблицы: Диаграмма Венна Диаграмма Венна...
-
Необходимо найти минимальное значение целевой функции F = 4x1+18x2 > min, при системе ограничений: X1+4x2?14(1) X1+6x2?15(2) X1+x2?5(3)...
-
Как известно решение задач симплексным методом применяется очень часто. Это связано с тем, что симплексный метод подходит для решения широкого круга...
-
Динамическое программирование Динамическое программирование -- один из разделов оптимального программирования, в котором процесс принятия решения и...
-
В начале пятилетнего периода работы предприятию выделена сумма в C руб. для приобретения нового оборудования. Стоимость одного комплекта оборудования...
-
Изучение теоретических вопросов анализа чувствительности оптимального решения ЗЛП к вариациям некоторых параметров задачи и введению нового ограничения....
-
Второй раздел курсовой работы посвящен особенностям постановки и решения общей задачи линейного программирования, а именно, транспортной задаче (ТЗЛП)....
-
Элементы матричного анализа - Методы решения системы линейных уравнений
Вектором, как на плоскости, так и в пространстве, называется направленный Отрезок , то есть такой Отрезок , один из концов которого выделен и называется...
-
Уравнение линии на плоскости - Методы решения системы линейных уравнений
Как известно, любая точка на плоскости определяется двумя координатами в какой - либо системе координат. Системы координат могут быть различными в...
-
Определение . Алгебраическим дополнением минора матрицы называется его Дополнительный минор , умноженный на (-1) в степени, равной сумме номеров строк и...
-
Системы линейных уравнений - Методы решения системы линейных уравнений
Системой m линейных уравнений с n неизвестными называется система вида Где aIj и bI (i=1,...,m; b=1,...,n) - некоторые известные числа, а x1,...,xN -...
-
Некоторые особенности решения задач нелинейного программирования - Экономико-математические методы
Для решения ЗНП существенно знать: 1) выпукло или не выпукло множество допустимых решений задачи; 2) является ли целевая функция выпуклой или вогнутой...
-
Вариации коэффициентов целевой функции ЗЛП приводят к изменению направления вектора градиента. Так как при этом не затрагивается допустимое множество, то...
-
Модели линейного программирования. Основные определения Еще одним классом задач экономико-математического моделирования являются задачи линейного...
-
Несмотря на требование линейности функций критериев и ограничений, в рамки линейного программирования попадают многочисленные задачи распределения...
-
При решении экономических задач часто анализировать ситуации, в которых сталкиваются интересы двух или более конкурирующих сторон, преследующих различные...
-
Линейное программирование в экономике - Экономико-математические методы
Задача о наилучшем использовании ресурсов. Пусть некоторая производственная единица (цех, завод, фирма и т. д.), исходя из конъюнктуры рынка, технических...
-
Линейное программирование, Общая задача линейного программирования - Экономико-математические методы
Термин "линейное программирование" впервые появился в 1951 г. в работах американских ученых (Дж. Данциг, Т. Купманс), а первые исследования по линейному...
-
Необходимость введения нового ограничения может возникнуть, например, когда первоначально для сокращения затрат машинного времени некоторые интуитивно...
-
Пусть имеется оптимизационная задача вида: (1) (2) (3) - задан(4) Здесь предполагается, что FJ(xJ,yJ)>0 для всех допустимых значений xJ,yJ. В этом случае...
-
Задачи с ограничениями в виде равенств - Линейное программирование в экономике
Рассмотрим общую задачу оптимизации, содержащую несколько ограничений в виде равенств: Минимизировать При ограничениях, k=1,...,n Эта задача в принципе...
-
Критерии оптимальности в задачах с ограничениями - Линейное программирование в экономике
Ряд инженерных задач связан с оптимизацией при наличии некоторого количества ограничений на управляемые переменные. Такие ограничения существенно...
-
ОБЩАЯ ПОСТАНОВКА ЗАДАЧИ ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ (ЗЛП) - Линейное программирование в экономике
Линейное программирование - направление математики, изучающее методы решения экстремальных задач, которые характеризуются линейной зависимостью между...
-
Проверить ряд на наличие выбросов методом Ирвина, сгладить методом простой скользящее средней с интервалом сглаживания 3, методом экспоненциального...
-
Пусть u = f(x, y) - функция, определенная в области w. Рассмотрим точку М(х, у) О w и некоторое направление l, определяемое направляющими косинусами Cosa...
-
Основные формулы интегрирования (табличные интегралы) - Методы решения системы линейных уравнений
1. ?dx = x+C 2. ?xNDx = (xN+1/(n+1))+C (n?-1) 3. ?(dx/x) = ln(x)+C 4. ?aXDx = aXLn(a)+C 5. ?eXDx = eX +C 6. ?sin(x)dx = -...
-
Решим прямую задачу линейного программирования симплексным методом, с использованием симплексной таблицы. Определим максимальное значение целевой...
-
Известно оптимальное решение X*=(0;0;1;1) задачи линейного программирования: Составьте двойственную задачу и найдите ее оптимальное решение по теореме...
-
Производной. - Методы решения системы линейных уравнений
Наиболее просто основные теоремы дифференциального исчисления формулируются для гладких функций. [ Править ] Производные и гладкие функции Пусть функция...
-
Экономико-математические методы и моделирование в землеустройстве позволяют решать большой круг задач, связанных с оптимизацией территориальной...
-
Области применения линейного программирования - Оптимальное программирование
Особенно широкое применение методы и модели линейного программирования получили при решении задач экономии ресурсов (выбор ресурсосберегающих технологий,...
-
Собственно-корреляционные параметрические методы изучения связи - Основы эконометрики
Измерение тесноты и направления связи является важной задачей изучения и количественного измерения взаимосвязи социально-экономических явлений. Оценка...
Параметрическое линейное программирование - Методы линейного программирования