Методы построения гамильтоновых циклов в графе, Алгебраический метод построения гамильтоновых циклов - Гамильтоновы циклы
Пока неизвестно никакого простого критерия или алгебраического метода, позволяющего ответить на вопрос, существует или нет в произвольном графе G гамильтонов цикл. Критерии существования, данные выше, представляют теоретический интерес, но являются слишком общими и не пригодны для произвольных графов, встречающихся на практике. Алгебраические методы определения гаильтоновых циклов не могут быть применены с более чем несколькими десятками вершин, так как они требуют слишком большого времени работы и большой памяти компьютера. Более приемлемым является способ Робертса и Флореса, который не предъявляет чрезмерных требований к памяти компьютера, но время в котором зависит экспоненциально от числа вершин в графе. Однако другой неявный метод перебора имеет для большинства типов графов очень небольшой показатель роста времени вычислений в зависимости от числа вершин. Он может быть использован для нахождения гамильтоновых циклов в очень больших графах.
Гамильтоновый графа цикл алгебраический
Алгебраический метод построения гамильтоновых циклов
Этот метод включает в себя построение всех простых цепей с помощью последовательного перемножения матриц. "Внутреннее произведение вершин" цепи x1, x2, ..., xK-1, xK определяется как выражение вида x2*x3* ... xK-1, не содержащее две концевые вершины x1 и xK. "Модифицированная матрица смежности" B=[? (i, j)] - это (n?n) - матрица, в которой ? (i, j) - xJ, если существует дуга из xI в xJ и нуль в противном случае. Предположим теперь, что у нас есть матрица PL = [pL(i, j)], где pL(i, j) - сумма внутренних произведений всех простых цепей длины L (L?1) между вершинами xI и xJ для xI?xJ. Положим pL(i, i)=0 для всех i. Обычное алгебраическое произведение матриц определяется как
B*PL=P'L+1=[p'L+1(s, t)]
Т. е. p'L+1(s, t) является суммой внутренних произведений всех цепей из xS в xT длины l+1. Так как все цепи из xK в xT, представленные внутренними произведениями из pL(k, t), являются простыми, то среди цепей, получающихся из указанного выражения, не являются простыми лишь те, внутренние произведения которых в pL(k, t) содержат вершину xS. Таким образом, если из p'L+1(s, t) исключить все слагаемые, содержащие xS (а это можно сделать простой проверкой), то получим pL+1(s, t). Матрица PL+1=[pL+1(s, t)], все диагональные элементы которой равны 0, является тогда матрицей всех простых цепей длины L+1.
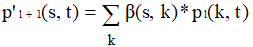
Вычисляя затем B*PL+1, находим PL+2 И т. д., пока не будет построена матрица PN-1, дающая все гамильтоновы цепи (имеющие длину n-1) между всеми парами вершин. Гамильтоновы циклы получаются тогда сразу из цепей в PN-1 И тех дуг из G, которые соединяют начальную и конечную вершины каждой цепи. С другой стороны, гамильтоновы циклы даются членами внутреннего произведения вершин, стоящими в любой диагональной ячейке матрицы B*PN-1 (все диагональные элементы этой матрицы одинаковые).
Очевидно, что в качестве начального значения матрицы P (т. е. P1) следует взять матрицу смежности A графа, положив все ее диагональные элементы равными нулю.
Недостатки этого метода совершенно очевидны. В процессе умножения матриц (т. е. когда L увеличивается) каждый элемент матрицы PL будет состоять из все большего числа членов вплоть до некоторого критического значения L, после которого число членов снова начнет уменьшаться. Это происходит вследствие того, что для малых значений L и для графов, обычно встречающихся на практике, число цепей длины L+1, как правило, больше, чем число цепей длины L, а для больших значений L имеет место обратная картина. Кроме того, так как длина каждого члена внутреннего произведения вершин увеличивается на единицу, когда L увеличивается на единицу, то объем памяти, необходимый для хранения матрицы PL, растет очень быстро вплоть до максимума при некотором критическом значении L, после которого этот объем снова начинает уменьшаться.
Похожие статьи
-
Условия существования гамильтонова цикла - Гамильтоновы циклы
В отличие от эйлеровых графов, где имеется критерий для графа быть эйлеровым, для гамильтоновых графов такого критерия нет. Более того, задача проверки...
-
Задачи, связанные с поиском гамильтоновых циклов - Гамильтоновы циклы
В ряде отраслей промышленности возникает следующая задача планирования. Нужно произвести n продуктов, используя единственный тип аппаратуры. Аппарат...
-
РЕШЕНИЕ ЗАДАЧИ О КОММИВОЯЖЕРЕ МЕТОДОМ ВЕТВЕЙ И ГРАНИЦ: ОСНОВНАЯ СХЕМА - Задача коммивояжера
Пусть - конечное множество и - вещественно-значная функция на нем; требуется найти минимум этой функции и элемент множества, на котором этот минимум...
-
Гамильтоновы циклы, Основные понятия и определения - Гамильтоновы циклы
Название "гамильтонов цикл" произошло от задачи "Кругосветное путешествие" предложенной ирландским математиком Вильямом Гамильтоном в 1859 году. Нужно...
-
Определение . Алгебраическим дополнением минора матрицы называется его Дополнительный минор , умноженный на (-1) в степени, равной сумме номеров строк и...
-
ОПРЕДЕЛЕНИЕ МЕТОДА ФАКТОРНОГО АНАЛИЗА И ЧИСЛА ФАКТОРОВ - Многомерный статистический анализ
Определение метода факторного анализа. Различные методы факторного анализа различаются в зависимости от подходов, которые используются для выделения...
-
Датой рождения метода Монте-Карло принято считать 1949 г., когда появилась статья под названием "The Monte Carlo method". Создателями этого метода...
-
Построение исходного опорного плана - Экономико-математические методы
Моделирование экономический математический опорный Построение опорных планов, а также их преобразование будем производить непосредственно в...
-
Методы построения функций принадлежности нечетких множеств - Нечеткая логика
В приведенных выше примерах использованы прямые методы, когда эксперт или просто задает для любого x?E значение ?A(x), или определяет функцию...
-
Методы построения решений по математическим моделям - Математическое моделирование в электромеханике
Системы дифференциальных уравнений, полученные для конкретных ти-пов электрических машин, содержат в скрытом виде исчерпывающую инфор-мацию о всех...
-
Итак, создав из трубочек и лески модель трехмерной проекции четырехмерного гиперкуба (3ПГК-4) (см. фотографию 1), приступим к построению 3ПГК-4 на...
-
Построение графа рынка России - Использование квази-клик для анализа графа рынка России
Для начала работы с алгоритмической частью требуется построить граф рынка. Для того, чтобы проанализировать правильность подхода с применением...
-
Счетные и несчетные множества - Методы решения системы линейных уравнений
Пусть, например, А и В Ї некоторые множества. Тогда их возможные взаимоотношения можно рассмотреть в виде таблицы: Диаграмма Венна Диаграмма Венна...
-
Введение, Основные положения - Эволюционные процедуры решения комбинаторных задач на графах
Среди набора комбинаторно-логических задач на графах важное место занимает проблема определения паросочетаний, раскраски графа, выделения в графе...
-
Ранговый метод - Ранговый метод оценивания параметров регрессионной модели
Метод наименьших квадратов широко применяется для оценки параметров линейной регрессии, поскольку достаточно прост в вычислении и при предположении о...
-
Введение - Методы экономико-математического моделирования
Экономико-математическое моделирование является неотъемлемой частью любого исследования в области экономики. Бурное развитие математического анализа,...
-
Метод дихотомии требует менее всего итераций цикла для получения корней уравнения с заданной точностью. Если расчет ведется без помощи ЭВМ, то это...
-
Важной задачей статистики является разработка методики статистической оценки социально-экономических явлений, которая осложняется тем, что многие...
-
Элементы матричного анализа - Методы решения системы линейных уравнений
Вектором, как на плоскости, так и в пространстве, называется направленный Отрезок , то есть такой Отрезок , один из концов которого выделен и называется...
-
РЕШЕНИЕ ЗАДАЧИ О КОММИВОЯЖЕРЕ МЕТОДОМ ВЕТВЕЙ И ГРАНИЦ. ПРИМЕРЫ - Задача коммивояжера
Рассмотрим конкретный пример реализации метода ветвей и границ для решения задачи о коммивояжере. Итак, требуется найти легчайший простой основный...
-
Формирование З -областей в матрице R осуществляется в процессе ее эволюционной модификации. Эволюционная модификация матрицы R производится путем...
-
Алгоритм решения ТЗ методом потенциалов - Экономико-математические методы
Построить опорный план по одному из правил. Проверить план на невырожденность. Если полученный план вырожденный, формально заполняют нулями некоторые из...
-
Решение транспортной задачи методом потенциалов - Математическая модель решения транспортной задачи
Этот метод позволяет автоматически выделять циклы с отрицательной ценой и определять их цены. Пусть имеется транспортная задача с балансовыми условиями...
-
Существует три основных типа окислительно-восстановительных реакций: 1. Если окислитель и восстановитель находятся в молекулах различных веществ, то...
-
Построение модели на реальных данных - Ранговый метод оценивания параметров регрессионной модели
Для построения линейной регрессионной модели на основе реальных данных при помощи рангового метода оценивания параметров был выбран достаточно известный...
-
Правила построения рядов динамики - Методы анализа основной тендеции развития в рядах динамики
При построении динамических рядов необходимо соблюдать определенные правила: основным условием для получения правильных выводов при анализе рядов...
-
При написании программ численного интегрирования желательно, чтобы для любой функции распределение узлов являлось оптимальным или близким к нему. Однако...
-
Построение теоретической функции методом наименьших квадратов Задание 1 Используя метод наименьших квадратов найти оценки коэффициентов регрессионной...
-
Метод построения горизонтальной проекции 3ПГК-n - "Начала" многомерной геометрии
3.15 на примере построения трехмерной проекции пятимерного гиперкуба (3ПГК-5). Рис. 3.15 (см. продолжение). Этапы Построения Горизонтальной Проекции...
-
Итак, модели, которые будут дальше анализироваться, и получены с помощью Первого метода - проведения теста для выделения наиболее дескриптивных...
-
Структурная целостность (связность) В системно-физическом плане внутренняя связность (связность) системы проявляется в наличии внутренних...
-
Введение, Методы экстраполяции - Формализованные методы прогнозирования
К формализованным методам относятся методы экстраполяции и методы моделирования. Они базируются на математической теории. Среди методов экстраполяции...
-
Методы непараметрической статистики - Основы теории систем и системного анализа
Использование классических распределений случайных величин обычно называют "параметрической статистикой" - мы делаем предположение о том, что...
-
Классификация экономико-математических методов - История развития методов и моделей в экономике
Велика роль математических моделей при описании экономических объектов и процессов, что, безусловно, подтверждается историей развития этого направления...
-
Метод конечных разностей -- широко известный и простейший метод интерполяции. Его суть заключается в замене дифференциальных коэффициентов уравнения на...
-
Заключение - Моделирование систем массового обслуживания с использованием метода Монте-Карло
Метод Монте-Карло можно определить как метод моделирования случайных величин с целью вычисления характеристик их распределений. Возникновение идеи...
-
В этом случае лучшим считается вариант, у которого суммарная величина отдельных целевых функций принимает максимальное значение: F Max = = max...
-
В зависимости от содержания задачи может быть два случая: когда ребра графа G единичной длины; когда ребра графа произвольной длины. Для каждого из этих...
-
Для достижения поставленной цели предприятию требуются материалы, оборудование, энергия, рабочая сила и другие ресурсы. Каждое предприятие такими...
-
Метод Монте-Карло используют для вычисления интегралов, в особенности многомерных, для решения систем алгебраических уравнений высокого порядка, для...
Методы построения гамильтоновых циклов в графе, Алгебраический метод построения гамильтоновых циклов - Гамильтоновы циклы