Введение, Основные положения - Эволюционные процедуры решения комбинаторных задач на графах
Среди набора комбинаторно-логических задач на графах важное место занимает проблема определения паросочетаний, раскраски графа, выделения в графе внутренне устойчивого множеств вершин и клик. Эвристические алгоритмы решения данных задач применяются при проектировании инженерных сетей, коммуникаций, построения систем поддержки принятия решений в неопределенных условиях, проектировании СБИС и т. п. Задачи такого типа относятся к переборным задачам с экспоненциальной временной сложностью. В этой связи разрабатывают различные эвристики для построения алгоритмов с полиномиальной временной сложностью. Существуют алгоритмы определения паросочетаний в графе, основанные на использовании потоков в сетях [Андерсон, 2003], [Кормен и др., 2000], имитационного моделирования [Свами и др., 1984], генетического поиска [Курейчик и др., 2003] И других эвристиках. В работе предлагается новый метод определения максимального паросочетания в графе, основанный на идеях поисковой адаптации.
Основные положения
Одной из широко востребованных задач целочисленного программирования является задача о паросочетании максимальной мощности, рассматриваемой в комбинаторном направлении теории графов. Паросочетанием графа G=(X, U) называет подмножество таких ребер U'U, что любые два ребра UK,uL U 'не имеют общих вершин, т. е. не смежны. Паросочетание максимальной мощности определяется как паросочетание, состоящее из максимального числа ребер [Андерсон, 2003].
Процедура нахождения максимального паросочетания в графе входит в состав большого числа алгоритмов, решающих различные задачи, [Макконнел, 2004]. Часто эта процедура используется в итерационных структурах. Это предъявляет повышенные требования к качеству и времени решения задачи нахождения максимального паросочетания.
Существующее в настоящее время большее количество алгоритмов нахождения максимального паросочетания обеспечивают приемлемые результаты при решении задач малой и средней сложности. Возникшие потребности в решении задач большой и очень большой размерности является побудительным мотивом исследований и разработок новых эффективных алгоритмов. Анализ литературы показывает, что наиболее успешными в этих условиях являются методы, основанные на моделировании эволюционных процессов [Лебедев и др., 2005].
В работе излагается методика представления решения на базе матрицы смежности графа, адаптивные механизмы видоизменения матрицы смежности, и рассматривается структура процесса эволюционной модификации матрицы смежности для решения задачи нахождения максимального паросочетания в графе и раскраски графа.
Пусть дан граф G=(X, U) (рис. 1). U={uI| i=1,2,...,9}. Паросочетание такого графа определяется как множество ребер, не имеющих общих вершин. Например: паросочетание P={u1, u4, u7, u9}. Построим граф GD=(U, V) - двойственный для графа G. Вершины графа GD - соответствуют ребрам графа G. Пара вершин (uI, uJ) в графе GD связаны ребром в том и только в том случае, если в графе G пара ребер (uI, uJ) смежны, т. е. инциденты одной вершине.
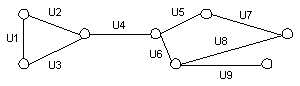
Рис. 1. Пример графа
Для примера, представленного на рис. 1, двойственный граф GD имеет вид, представленный на рис. 2.
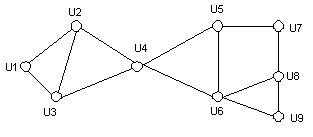
Рис. 2. Двойственный граф GD
Множество X0 вершин графа G=(X, U) называется внутренне устойчивым, если любые две вершины XI X0 и XJ X0 не являются смежными. Максимальное число вершин во внутренне устойчивом множестве графа G называется числом внутренней устойчивости и обозначается как Б(G). Иногда число внутренней устойчивости называют также числом независимости графа G.
Подмножество вершин P={u1, u4, u7, u9} Является внутренне-устойчивым, т. к. любые две вершины подмножества P не смежны. Таким образом, паросочетанию графа G соответствует внутренне-устойчивое подмножество двойственного графа GD.
Максимальному по мощности паросочетанию графа G соответствует предельное внутренне-устойчивое подмножество (содержащее наибольшее число вершин) двойственного графа GD.
Построим для двойственного графа GD матрицу смежности R (Рис. 3). Переставим все столбцы и строки помеченные элементами некоторого внутренне-устойчивого подмножества P таким образом, чтобы они располагались рядом друг с другом начиная с левой (верхней) стороны матрицы. Для нашего примера модифицированная матрица R имеет вид, представленный на рис. 4. Анализ состояния матрицы смежности показывает что если столбцы матрицы с номерами от L до L+m помечены элементами, образующими внутренне-устойчивое подмножество, то симметрично относительно главной диагонали матрицы R на пересечении столбцов и строк матрицы с номерами от L до (L+m -1) формируется область PI Квадратной формы размером M*m, элементы которой имеют нулевое значение. Назовем такую область - областью. В приведенном примере - область - это область, образованная при пересечении 1-4 столбца с 1-4 строкой. Столбцы и строки помечены элементами 1,4,7,9. PI=PI(l, m), где L - номер первого столбца (и первой строки), с которого начинается - область PI, M - число столбцов и строк, на пересечении которых образована - область PI. Для нашего примера P1=P1(1,4).
Матрица смежность граф комбинаторный
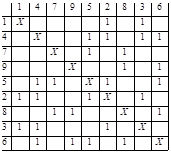
Рис. 3. Исходная матрица смежности Рис.4. Матрица смежности с построенной - областью
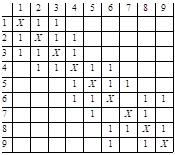
Таким образом, если в результате некоторой перестановки строк и столбцов матрицы смежности образуется - область PI(l, m), то это значит, что элементы, которыми помечены столбцы и строки с номерами от L до (l+m-1), образуют внутренне-устойчивое подмножество UI. И если операция производилась на графе GD, двойственном к G, то подмножеству UI Соответствует паросочетание в G. Отсюда схема нахождения в графе G паросочетания максимальной мощности выглядит так.
Строится граф GD , двойственный к графу G. Путем перестановок строк и столбцов матрицы смежности R графа GD формируется - область PI(l, m) с максимально возможным значением параметра M. Множество элементов UI, которыми в матрице смежности R помечены столбцы с номерами от L до (l+m-1), будут составлять максимальное паросочетание в графе G.
Раскраской графа называется такое приписывание цветов его вершинам, что никакие две смежные вершины не получают одинакового цвета. Минимальное число цветов, в которое можно раскрасить граф G, называется хроматическим числом и обозначается ч(G) [Курейчик, 1990].
Будем считать, что - область PI(l, m) покрывает строки и столбцы матрицы смежности R с номерами от L до (l+m-1). Назовем две - области PI(lI,mI) и PJ(lJ,mJ) смежными друг к другу, если LJ=lI+mI. Пересечение двух смежных - областей равно. Если в результате перестановок столбцов и строк матрицы R образуется цепочка из S последовательно прилегающих друг к другу, то есть смежных - областей, объединение которых покрывает все столбцы и строки матрицы R, то можно считать, что в графе G выделено S внутренне-устойчивых подмножеств вершин и, следовательно, граф можно раскрасить в S цветов.
Таким образом задача раскраски графа сводится к задаче формирования в матрице смежности графа цепочки - областей с вышеперечисленными свойствами. Формирование цепочки с минимальным числом - областей соответствует раскраске в минимальное число цветов.
На рис. 4 в матрице R сформирована цепочка из 3-х областей. Следовательно, граф раскрашивается в 3 цвета. {u1, u4, u7, u9} - 1 цвет, {u5, u2, u8} - 2 цвет, {u3, u6} - 3 цвет.
Рассмотрим задачу о Клике. Кликой графа G называется максимальное по включению множество X0 вершин графа, любые две из которых являются смежными. Нетрудно видеть, что при переходе от графа G к его дополнению каждая клика в G переходит в независимое множество в. Отсюда следует, что задача выделения клики в графе G сводится к задаче выделения независимого множества вершин в графе, являющегося дополнением графа G.
Таким образом в основе процедур построения максимального паросочетания, раскраски графа, выделения в графе внутренне устойчивого множеств вершин и клик лежит одна общая процедура формирования З-областей в матрице смежности графа.
Похожие статьи
-
Формирование З -областей в матрице R осуществляется в процессе ее эволюционной модификации. Эволюционная модификация матрицы R производится путем...
-
РЕШЕНИЕ ЗАДАЧИ О КОММИВОЯЖЕРЕ МЕТОДОМ ВЕТВЕЙ И ГРАНИЦ: ОСНОВНАЯ СХЕМА - Задача коммивояжера
Пусть - конечное множество и - вещественно-значная функция на нем; требуется найти минимум этой функции и элемент множества, на котором этот минимум...
-
Наличие особых ситуаций на террайне зависит от характеристик его сложности. Ниже приведена возможная классификационная схема характеристик сложности...
-
Задача поиска маршрутов в графе (путей в орграфе)
Задача поиска маршрутов в графе (путей в орграфе) Алгоритм Тэрри поиска маршрута в связном графе, соединяющем вершины и. Правила. 1) Идя по произвольному...
-
РЕШЕНИЕ ЗАДАЧИ О КОММИВОЯЖЕРЕ МЕТОДОМ ВЕТВЕЙ И ГРАНИЦ. ПРИМЕРЫ - Задача коммивояжера
Рассмотрим конкретный пример реализации метода ветвей и границ для решения задачи о коммивояжере. Итак, требуется найти легчайший простой основный...
-
О клике. Определим формально задачу поиска максимальной клики, согласно статьи On the maximum quasi-clique problem [17]. Пусть G=(V, E) - простой...
-
Введение - Приложение интегрального и дифференциального исчисления к решению прикладных задач
Целью данной курсовой работы является самостоятельное изучение следующих разделов высшей математики: задачи линейного программирования (симплексный и...
-
Необходимость введения нового ограничения может возникнуть, например, когда первоначально для сокращения затрат машинного времени некоторые интуитивно...
-
Вариации коэффициентов целевой функции ЗЛП приводят к изменению направления вектора градиента. Так как при этом не затрагивается допустимое множество, то...
-
Метод дифференциальных рент для решения транспортной задачи - Формирование оптимального штата фирмы
Для решения транспортных задач используется несколько методов. Рассмотрим решение с помощью метода дифференциальных рент. При нахождении решения...
-
При решении экономических задач часто анализировать ситуации, в которых сталкиваются интересы двух или более конкурирующих сторон, преследующих различные...
-
Введение - Моделирование крупномасштабной транспортной сети предфрактальными графами
Транспорт - важный стратегический комплекс, в значительной степени определяющий мощь экономики страны и обеспечивающий нужды общества в перемещении людей...
-
Введение - Использование квази-клик для анализа графа рынка России
Графы, состоящие из вершин и ребер, представляют удобный инструмент моделирования для изучения различных сетевых структур, в том числе, социальных сетей,...
-
Рассмотрим взвешенный предфрактальный граф, порожденный затравкой и K процессоров, где. Параллельный алгоритм выделения дольного графа основан на...
-
О квази-клике. - Использование квази-клик для анализа графа рынка России
Квази-клика - представляет собой релаксацию строгого условия полноты клики, то есть допускается отсутствие некоторых ребер в искомом подграфе. На данный...
-
Ограничение чувствительность задача программирование Вариации правых частей ограничений приводят к изменению области допустимых решений ЗЛП, в действии...
-
Введение - Решение оптимизационных экономических задач методами линейного программирования
Линейное программирование является составной частью раздела математики, который изучает методы нахождения условного экстремума функции многих переменных...
-
Оптимизация инвестиционного портфеля (ИП) [Дубровин и др., 2008], [Мищенко и др., 2002], [Серов, 2000] является одной из важных экономических задач,...
-
Любое частное решения уравнения (1) на координатной плоскости х0у изображено в виде графика функции у=у (х, с) (с=const). В теории дифференциальных...
-
Симплекс-метод - Приложение интегрального и дифференциального исчисления к решению прикладных задач
Теория: Другой способ решения задач линейного программирования - симплекс-метод. Он, в отличие от геометрического, является полностью аналитическим, что...
-
Это раздел математического программирования, изучающий методы решения таких экстремальных задач, в которых результаты (эффективность) возрастают или...
-
ФУНКЦИИ, Основные понятия - Свойства функций
Основные понятия При изучении различного рода явлений приходится иметь дело с совокупностью переменных величин, которые связаны между собой таким...
-
Матрицы и определители - Методы решения системы линейных уравнений
Определение. Матрицей размера mn, где m - число строк, n - число столбцов, называется таблица чисел, расположенных в определенном порядке. Эти числа...
-
Определим понятие предфрактального графа индуктивно. Обозначим через - конечный связный n-вершинный граф с множеством вершин и множеством ребер, который...
-
Элементы матричного анализа - Методы решения системы линейных уравнений
Вектором, как на плоскости, так и в пространстве, называется направленный Отрезок , то есть такой Отрезок , один из концов которого выделен и называется...
-
Ранг матрицы. - Методы решения системы линейных уравнений
Как было сказано Выше , минором матрицы порядка s называется определитель матрицы, образованной из элементов исходной матрицы, находящихся на пересечении...
-
Определители (детерминанты) - Методы решения системы линейных уравнений
Определение. Определителем квадратной матрицы А= называется число, которое может быть вычислено по элементам матрицы по формуле: Det A = , где (1) М1к -...
-
В настоящее время Российская Федерация входит в состав ВТО, в связи с чем, для устойчивого развития, для надежности, для стойкости [1, 2] появляется...
-
Пусть функция определена в промежутке Х (рис.1). Исходя из некоторого значения независимой переменной, придадим ему приращение, не выводящее его из...
-
Условие задачи. Пусть имеются n кандидатов для выполнения этих работ. Назначение кандидата i на работу j связано с затратами CIj (i, j = 1,2,..., n)....
-
Изучение теоретических вопросов анализа чувствительности оптимального решения ЗЛП к вариациям некоторых параметров задачи и введению нового ограничения....
-
Задача Джонсона о двух станках Рассмотрим задачу последовательной обработки на двух машинах N различных деталей, если известно время Ai и Bi обработки...
-
Опытным путем, задолго до появления молекулярно-кинетической теории, был открыт целый ряд законов, описывающих равновесные изопроцессы в идеальном газе....
-
Некоторые особенности решения задач нелинейного программирования - Экономико-математические методы
Для решения ЗНП существенно знать: 1) выпукло или не выпукло множество допустимых решений задачи; 2) является ли целевая функция выпуклой или вогнутой...
-
Решим прямую задачу линейного программирования симплексным методом, с использованием симплексной таблицы. Определим максимальное значение целевой...
-
Известно оптимальное решение X*=(0;0;1;1) задачи линейного программирования: Составьте двойственную задачу и найдите ее оптимальное решение по теореме...
-
Пусть на некотором отрезке [a, b] задана кусочно-монотонная функция f(x). Покажем, что данную функцию в точках ее непрерывности можно представить в виде...
-
Современные инженерные задачи оптимизации многокритериальные. Выделяют класс задач многоцелевой или многокритериальной оптимизации (класс МКО-задач). В...
-
Задача о загрузке рюкзака (задача о ранце) - Метод динамического программирования для решения задач
Постановка задачи. Пусть имеются N видов грузов с номерами. Единица груза j-го вида имеет все aJ. Если груз j-го вида берется в количестве xJ, то его...
-
Основные задачи анализа временных рядов - Динамические ряды
Принципиальные отличия временного ряда от последовательности наблюдений, образующих случайную выборку, заключаются в следующем: Во-первых, в отличие от...
Введение, Основные положения - Эволюционные процедуры решения комбинаторных задач на графах