Метод Рунге-Кутта - Методы решения обыкновенных дифференциальных уравнений

В модифицированном методе Эйлера для получения второй производной D2U(XI)/Dx2 используется конечно-разностная формула (6), включающая значения первой производной U'(XI) и U'(XI+H) в начальной и конечной
Точках шага. Если подобным же образом вычислить третью производную, рассчитав предварительно вторую производную в двух точках шага, то можно с помощью (3) построить расчетную формулу метода третьего порядка точности. Для этого потребуется определить первую производную U'(X) в дополнительной промежуточной точке между XI и XI + H.

Аналогичные рассуждения позволяют вывести расчетные формулы методов более высоких порядков, обеспечивающих заметное снижение погрешности решения. Однако на практике их реализация требует существенного повышения объема вычислений с использованием дополнительных промежуточных точек на каждом шаге.

Существуют и другие способы построения численных методов с высоким порядком точности. Один из них, применяемый при построении группы методов Рунге-Кутта, заключается в аппроксимации решения дифференциального уравнения суммой

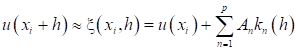
, (8)

Где AN - коэффициенты разложения, KN - последовательность функций

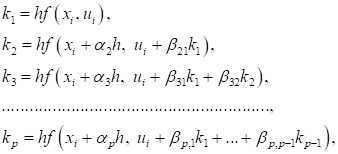
(9)

БN,вNm, 0 <M<N ? P - некоторые параметры.

Неизвестные параметрыAN,бN ивNmМожно выбрать из условия

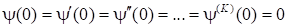
, (10)

Где функция ш(H)= U(XI+H) - о(XI,H) показывает отклонение приближенного решения о(XI,H) от точного U(XI+H). Увеличение параметраP в (8) позволяет сделать погрешность, связанную с заменой точного решения приближенным, как угодно малой.

Предположим, что P = 1. Тогда, подставляя (8) в (10), из условия
Ш(0) = ш'(0) = 0 получим A1 = 1 и ш''(0) ? 0, откуда

,

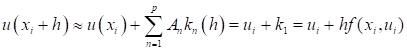
Что соответствует формуле Эйлера (5). Таким же образом можно получить формулы более высоких порядков точности, которые называют методами Рунге-Кутта.

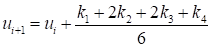
Одним из наиболее известных является вариант метода Рунге-Кутта, соответствующий P = 4. Это метод четвертого порядка точности, для которого ошибка на шаге имеет порядок H5. Его расчетные формулы имеют следующий вид:

,

Где

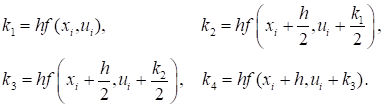
Рассмотренные выше метод Эйлера и его модификация по сути дела являются методами Рунге-Кутта первого и второго порядка соответственно. Несмотря на увеличение объема вычислений метод четвертого порядка имеет преимущество перед методами первого и второго порядков, так как он обеспечивает малую локальную ошибку. Это позволяет увеличивать шаг интегрирования H и, следовательно, сокращать время расчета.

Похожие статьи

• Описания методов решения:, Метод Эйлера - Методы решения обыкновенных дифференциальных уравнений

  Метод Эйлера Расчетную формулу метода Эйлера можно получить, используя разложение функции U ( X ) в ряд Тейлора в окрестности некоторой точки X I : . (1)...

• Постановка задачи, Основные сведения - Комплексное исследование численных методов для задачи решения нелинейных уравнений

  Провести комплексное исследование численных методов для задачи решения нелинейных уравнений. 1. Решить нелинейные уравнения А) ; Б) ; В) . 2....

• Модифицированный метод Эйлера - Методы решения обыкновенных дифференциальных уравнений

  Точность метода Эйлера можно существенно повысить, улучшив аппроксимацию U ( X ) на рассчитываемом шаге. Для этого при разложении U ( X ) в ряд Тейлора...

• Счетные и несчетные множества - Методы решения системы линейных уравнений

  Пусть, например, А и В Ї некоторые множества. Тогда их возможные взаимоотношения можно рассмотреть в виде таблицы: Диаграмма Венна Диаграмма Венна...

• Результаты исследования, Вычисления для следующих входных данных, Сравнение результатов - Численное нахождение корня уравнения методом Рунге-Кутта

  Вычисления для следующих входных данных F=1000H m=200 кг m'=1 кг/сек k=2 t0=0 сек V0=0 м/сек B=50 n=50 V1 (t) - результаты, полученные с помощью...

• Задание для исследования - Численное нахождение корня уравнения методом Рунге-Кутта

  Исследовать решение обыкновенных дифференциальных уравнений методом Рунге-Кутты. Подробное описание Метод этот пригоден для решения как одиночных...

• Геометрический смысл задачи Каши, Методы решения дифференциальных уравнений - Неопределенный интеграл

  Любое частное решения уравнения (1) на координатной плоскости х0у изображено в виде графика функции у=у (х, с) (с=const). В теории дифференциальных...

• Функции нескольких переменных. Предел и непрерывность. Частные производные. - Методы решения системы линейных уравнений

  Пусть u = f(x, y) - функция, определенная в области w. Рассмотрим точку М(х, у) О w и некоторое направление l, определяемое направляющими косинусами Cosa...

• Производной. - Методы решения системы линейных уравнений

  Наиболее просто основные теоремы дифференциального исчисления формулируются для гладких функций. [ Править ] Производные и гладкие функции Пусть функция...

• Анализ работы методов - Комплексное исследование численных методов для задачи решения нелинейных уравнений

  Метод дихотомии требует менее всего итераций цикла для получения корней уравнения с заданной точностью. Если расчет ведется без помощи ЭВМ, то это...

• Цель работы: Изучение методов решения обыкновенных дифференциальных уравнений - Методы решения обыкновенных дифференциальных уравнений

  Задание: Задание 1. Для охлаждения микропроцессора используется металлический теплоотводящий радиатор. Процесс передачи тепла от радиатора в окружающий...

• Системы линейных уравнений - Методы решения системы линейных уравнений

  Системой m линейных уравнений с n неизвестными называется система вида Где aIj и bI (i=1,...,m; b=1,...,n) - некоторые известные числа, а x1,...,xN -...

• Основные формулы интегрирования (табличные интегралы) - Методы решения системы линейных уравнений

  1. ?dx = x+C 2. ?xNDx = (xN+1/(n+1))+C (n?-1) 3. ?(dx/x) = ln(x)+C 4. ?aXDx = aXLn(a)+C 5. ?eXDx = eX +C 6. ?sin(x)dx = -...

• Функции и ее свойства - Методы решения системы линейных уравнений

  В современной математике понятие множества является одним из основных. Универсальность этого понятия в том, что под него можно подвести любую...

• Уравнение линии на плоскости - Методы решения системы линейных уравнений

  Как известно, любая точка на плоскости определяется двумя координатами в какой - либо системе координат. Системы координат могут быть различными в...

• Геометрический метод - Приложение интегрального и дифференциального исчисления к решению прикладных задач

  Теория: Применяется, как правило, для задач линейного программирования, содержащих не более 2 переменных. Суть геометрического метода сводится к...

• Автоколебания в химических реакциях, Вывод расчетных формул - Автоколебания в химических реакциях. Численные методы

  Модель Лефевра-Николиса описывает колебательные процессы в следующей цепочке химических реакций: Предполагается, что концентрации веществ A, B, D, E...

• Разложение правильной рациональной дроби на сумму простейших дробей. - Методы решения системы линейных уравнений

  Любая правильная рациональная дробь P(x)/Q(x) может быть единственным образом представлена в виде суммы простейших рациональных дробей. Для этого прежде...

• Вычисление интегралов методом Монте-Карло, Алгоритмы метода Монте-Карло для решения интегральных уравнений второго рода - Применение метода Монте-Карло в эконометрическом анализе

  Алгоритмы метода Монте-Карло для решения интегральных уравнений второго рода Пусть необходимо вычислить линейный функционал , Где, причем для...

• Элементы матричного анализа - Методы решения системы линейных уравнений

  Вектором, как на плоскости, так и в пространстве, называется направленный Отрезок , то есть такой Отрезок , один из концов которого выделен и называется...

• Элементарные преобразования, Миноры - Методы решения системы линейных уравнений

  Определение. Элементарными преобразованиями матрицы назовем следующие преобразования: 1) умножение строки на число, отличное от нуля; 2) прибавление к...

• Частные производные высших порядков - Методы решения системы линейных уравнений

  Пусть z=f(x, y). Тогда и - частные производные по переменным х и у. В некоторых случаях существуют снова от этих функций частные производные, называемые...

• Свойства операции умножения матриц - Методы решения системы линейных уравнений

  1)Умножение матриц не коммутативно, т. е. АВ ВА даже если определены оба произведения. Однако, если для каких - либо матриц соотношение АВ=ВА...

• Решение смешанной задачи для уравнения теплопроводности методом конечных разностей

  Решение смешанной задачи для уравнения теплопроводности методом конечных разностей 1. Цель работы Ознакомление с методами решения смешанных задач для...

• Некоторые особенности решения задач нелинейного программирования - Экономико-математические методы

  Для решения ЗНП существенно знать: 1) выпукло или не выпукло множество допустимых решений задачи; 2) является ли целевая функция выпуклой или вогнутой...

• Функции распределения вероятностей для параметров, описываемых обобщенными интервальными оценками - Метод представления знаний в интеллектуальных системах поддержки экспертных решений

  Пусть Dl, r() соответственно левые (правые) границы интервалов I, отвечающих на криволинейной трапеции ОИО значениям 0< < 1. Тогда интересующая нас...

• Ранг матрицы. - Методы решения системы линейных уравнений

  Как было сказано Выше , минором матрицы порядка s называется определитель матрицы, образованной из элементов исходной матрицы, находящихся на пересечении...

• Алгебраические дополнения, Обратная матрица, войства обратных матриц. - Методы решения системы линейных уравнений

  Определение . Алгебраическим дополнением минора матрицы называется его Дополнительный минор , умноженный на (-1) в степени, равной сумме номеров строк и...

• Матрицы и определители - Методы решения системы линейных уравнений

  Определение. Матрицей размера mn, где m - число строк, n - число столбцов, называется таблица чисел, расположенных в определенном порядке. Эти числа...

• Простейшие дроби и их интегрирование. - Методы решения системы линейных уравнений

  Рациональной дробью называется дробь вида P(x)/Q(x), где P(x) и Q(x) - многочлены. Рациональная дробь называется правильной, если степень P(x) ниже...

• Определители (детерминанты) - Методы решения системы линейных уравнений

  Определение. Определителем квадратной матрицы А= называется число, которое может быть вычислено по элементам матрицы по формуле: Det A = , где (1) М1к -...

• Метод дифференциальных рент для решения транспортной задачи - Формирование оптимального штата фирмы

  Для решения транспортных задач используется несколько методов. Рассмотрим решение с помощью метода дифференциальных рент. При нахождении решения...

• Особенности постановки и решения общей задачи линейного программирования - Определение оптимальной стратегии рыночного поведения с использованием макроэкономических методов и моделей

  Второй раздел курсовой работы посвящен особенностям постановки и решения общей задачи линейного программирования, а именно, транспортной задаче (ТЗЛП)....

• ЗАКЛЮЧЕНИЕ - Основные методы математического моделирования для принятия управленческих решений

  В данной работе поставленная цель была достигнута. Мы рассмотрели основные методы математического моделирования (принятия решений) на практике, а именно:...

• ВВЕДЕНИЕ, ЗАДАНИЕ 1 - Основные методы математического моделирования для принятия управленческих решений

  В экономической сфере деятельности в современных условиях большое значение имеет принятие решений. Для принятия экономических решений в нынешних условиях...

• Методы построения решений по математическим моделям - Математическое моделирование в электромеханике

  Системы дифференциальных уравнений, полученные для конкретных ти-пов электрических машин, содержат в скрытом виде исчерпывающую инфор-мацию о всех...

• Решение квадратных уравнений, Решение квадратных неравенств, Числовая функция и способы ее задания - Математика в современном мире

  Ответ: уравнение ax2+bx+c=0. Где а не равно нулю, называется квадратным. Чтобы его решить нужно вычислить дискриминант. D=b2 -4ac и сравнить его с нулем....

• Решение уравнений и построение графиков функций, содержащих выражения со знаком модуля - Решение уравнений и построение графиков функций, содержащих выражения со знаком модуля

  Выполнил: Шварц В. И. 9-Б класс Руководитель: Шагалина Д. Г. Межгорье 2005 Решение уравнений и неравенств, содержащих выражения под Знаком модуля Любое...

• Дифференциальные уравнения - Неопределенный интеграл

  Неопределенный интеграл дифференциальный дробь Однородные дифференциальные уравнения I порядка О: Дифференциальным уравнением I порядка называется...

• О периодических функциях - Действительные числа. Тригонометрические функции числового аргумента. Логарифмы. Частные случаи решения тригонометрических уравнений

  Если функция f(x) периодична с периодом Т, то по значениям этой функции на любом отрезке длины Т можно восстановить ее значения на всей числовой прямой....

Метод Рунге-Кутта - Методы решения обыкновенных дифференциальных уравнений

Предыдущая | Следующая