Декартовы прямоугольные координаты, Сферические координаты - Приложение интегрального и дифференциального исчисления к решению прикладных задач

Вычисление тройного интеграла в декартовых прямоугольных координатах сводится к последовательному вычислению одного однократного и одного двойного интегралов. Если область интегрирования ограничена снизу и сверху соответственно поверхностями: а с боков - прямым цилиндром, сечением которого плоскостью, параллельной плоскости

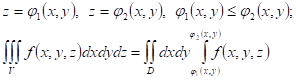
X0Y является область D, то:

Вычисление начинаем с внутреннего интеграла по переменной z, считая переменные x и y константами, а затем вычисляем двойной интеграл по проекции области V на плоскость X0Y.

Сферические координаты

Пусть

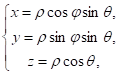
Где - радиус-вектор точки М, т. е. - расстояние от точки М до начала координат:

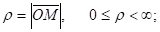
ц - угол между положительными направлением оси 0X и лучом (- проекция точки М на плоскость X0Y), ; и - угол между положительным направлением оси 0Z и радиус-вектором точки М (лучом ОМ), .

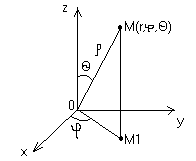
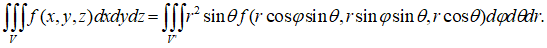
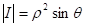
Тогда модуль якобиана: .

В сферических координатах:

Практика:

- сфера радиусом 4; - сфера радиусом 10; - конус второго порядка; - плоскости.

Изобразим проекции сфер и плоскостей на плоскость XOY:

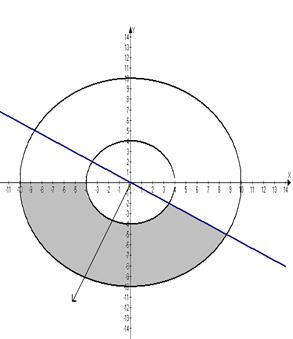
Перейдем к сферическим координатам:

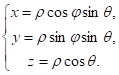
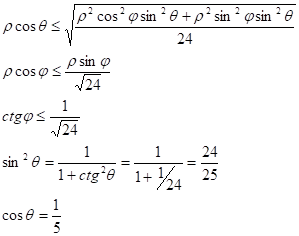
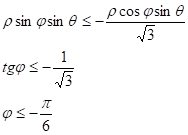
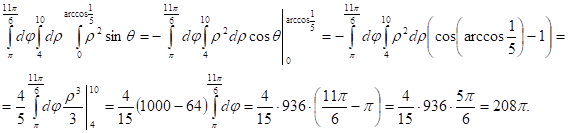
Ответ:

Задание № 6

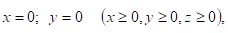
Найти массу тела ограниченного поверхностями: если плотность распределения массы равна

Теория:

Для вычисления массы тела применяем приложение тройного интеграла. В данном случае удобно применить переход к сферическим координатам.

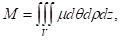
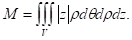
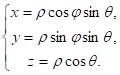
Практика:

Перейдем к сферическим координатам:

Ответ:

Похожие статьи

• Сферические координаты - Интегральное и дифференциальное исчисление

  Пусть Где R - радиус-вектор точки М , т. е. R - расстояние от точки М до начала координат: Ц - угол между положительными направлением оси 0X и лучом (-...

• Заключение, Список использованной литературы - Приложение интегрального и дифференциального исчисления к решению прикладных задач

  Итак, вышеизложенный материал наглядно рассматривает все интересующие нас разделы программы. Используя его, даже несведущий человек сможет овладеть...

• О разложении в ряд Фурье непериодической функции - Приложение интегрального и дифференциального исчисления к решению прикладных задач

  Пусть на некотором отрезке [a, b] задана кусочно-монотонная функция f(x). Покажем, что данную функцию в точках ее непрерывности можно представить в виде...

• Введение - Приложение интегрального и дифференциального исчисления к решению прикладных задач

  Целью данной курсовой работы является самостоятельное изучение следующих разделов высшей математики: задачи линейного программирования (симплексный и...

• Симплекс-метод - Приложение интегрального и дифференциального исчисления к решению прикладных задач

  Теория: Другой способ решения задач линейного программирования - симплекс-метод. Он, в отличие от геометрического, является полностью аналитическим, что...

• Геометрический метод - Приложение интегрального и дифференциального исчисления к решению прикладных задач

  Теория: Применяется, как правило, для задач линейного программирования, содержащих не более 2 переменных. Суть геометрического метода сводится к...

• Геометрический смысл задачи Каши, Методы решения дифференциальных уравнений - Неопределенный интеграл

  Любое частное решения уравнения (1) на координатной плоскости х0у изображено в виде графика функции у=у (х, с) (с=const). В теории дифференциальных...

• Симплекс - метод - Интегральное и дифференциальное исчисление

  Другой способ решения задач линейного программирования - симплекс-метод. Он, в отличие от геометрического, является полностью аналитическим, что...

• Введение - Интегральное и дифференциальное исчисление

  Эта курсовая работа является продолжением углубленного изучения высшей математики. В ней рассматриваются не пройденные нами темы за 3семестра изучения...

• Графическое решение задачи нелинейного программирования - Методика решения двойственных задач линейного программирования

  Так как целевая функция не является линейной, то эта задача является задачей нелинейного программирования. Найдем ее решение, используя геометрическую...

• Застосування подвійних інтегралів до задач геометрії, Обчислення маси пластинки, статичних моментів, моментів інерції і координат центра мас - Вища математика

  Площа плоскої області обчислюється за формулою (6) У полярній системі координат формула (6) має вигляд (7) Об'єм циліндричного тіла, обмеженою зверху...

• Некоторые особенности решения задач нелинейного программирования - Экономико-математические методы

  Для решения ЗНП существенно знать: 1) выпукло или не выпукло множество допустимых решений задачи; 2) является ли целевая функция выпуклой или вогнутой...

• Нелинейное программирование - Реферативно-прикладное исследование применения экономико-математических методов в решении задач производства (метод нелинейного программирования)

  Это раздел математического программирования, изучающий методы решения таких экстремальных задач, в которых результаты (эффективность) возрастают или...

• Геометрический метод - Интегральное и дифференциальное исчисление

  Теоретическое введение: Применяется, как правило, для задач линейного программирования, содержащих не более 2 переменных. Суть геометрического метода...

• Функции нескольких переменных. Предел и непрерывность. Частные производные. - Методы решения системы линейных уравнений

  Пусть u = f(x, y) - функция, определенная в области w. Рассмотрим точку М(х, у) О w и некоторое направление l, определяемое направляющими косинусами Cosa...

• Функция y=arccosx, ее график, свойства, Функция y=arctgx, ее график, свойства, Функция y=arcctgx, ее график, свойства, Решение уравнений sinx=a, частные случаи, Решение уравнений cosx=a, частнае случаи, Решение уравнений tgx=a, ctg=a, Решение тригонометрических уравнений, приводимых к квадратным, Решение простейших тригонометрических неравенств, Стереометрия. Основные понятия, обозначения, Аксиомы стереометрии - Математика в современном мире

  Ответ: Функция y=arctgx, ее график, свойства Ответ: Функция y=arcctgx, ее график, свойства Ответ: Решение уравнений sinx=a, частные случаи Ответ:...

• Геометрическая интерпретация и графическое решение ЗЛП - Экономико-математические методы

  Геометрическая интерпретация экономических задач дает возможность наглядно представить их структуру, выявить особенности и открывает пути исследования...

• Понятие производной, Основные правила и формулы дифференцирования, Геометрический смысл производной, Уравнение касательной и нормали к графику функции, угол между ними - Применение производной в решении геометрических задач

  Пусть функция определена в промежутке Х (рис.1). Исходя из некоторого значения независимой переменной, придадим ему приращение, не выводящее его из...

• Теоремы двойственности и их использование в задачах ЛП - Решение оптимизационных экономических задач методами линейного программирования

  Исходная задача: При ограничениях: Двойственной является следующая задача: При ограничениях: Число неизвестных в двойственной задаче равно 2....

• Решение задачи графическим методом - Математическое моделирование в менеджменте и маркетинге

  Необходимо найти максимальное значение целевой функции L(x)= 2x1+2x2 > max, при системе ограничений: 6x1+8x2?48, (1) 8x1+11x2?88, (2)...

• Постановка задачи, Основные сведения - Комплексное исследование численных методов для задачи решения нелинейных уравнений

  Провести комплексное исследование численных методов для задачи решения нелинейных уравнений. 1. Решить нелинейные уравнения А) ; Б) ; В) . 2....

• Решить графически задачу нелинейного программирования, Математическая модель задачи нелинейного программирования (ЗНП) - Методика решения двойственных задач линейного программирования

  Математическая модель задачи нелинейного программирования (ЗНП) (*) Для ЗНП в отличие от Задачи Линейного Программирования (ЗЛП) нет единого метода...

• Геометрический метод решения задач ЛП - Решение оптимизационных экономических задач методами линейного программирования

  Необходимо найти минимальное значение целевой функции F = 4x1+18x2 > min, при системе ограничений: X1+4x2?14(1) X1+6x2?15(2) X1+x2?5(3)...

• Основные методы решения задач, Решение задачи с помощью математического аппарата - Формирование оптимального штата фирмы

  Условие задачи. Пусть имеются n кандидатов для выполнения этих работ. Назначение кандидата i на работу j связано с затратами CIj (i, j = 1,2,..., n)....

• Стереометрические задачи - Применение производной в решении геометрических задач

  Рис.7 Задача 1.Определить наибольший объем цилиндра, вписанного в конус с радиусом основания и высотой [4]. Решение. Обозначим радиус основания...

• Решение геометрических задач на нахождение наибольшего и наименьшего значений с помощью производной, Планиметрические задачи - Применение производной в решении геометрических задач

  Планиметрические задачи Задача 1.Написать уравнения касательной и нормали к графику функциив данной точке, если: [3]. Решение. Уравнение касательной...

• Анализ чувствительности оптимального решения ЗЛП к вариациям коэффициентов целевой функции., Графический способ анализа чувствительности оптимального решения к вариациям C[j - Исследование чувствительности оптимального решения задачи линейного программирования к вариациям ее параметров и введению нового ограничения

  Вариации коэффициентов целевой функции ЗЛП приводят к изменению направления вектора градиента. Так как при этом не затрагивается допустимое множество, то...

• Решение задачи с помощью прикладных программ, Технология разработки формы для ввода исходных данных средствами VBA - Формирование оптимального штата фирмы

  Технология разработки формы для ввода исходных данных средствами VBA Для разработки формы ввода исходных данных необходимо отобразить вкладку...

• Метод дифференциальных рент для решения транспортной задачи - Формирование оптимального штата фирмы

  Для решения транспортных задач используется несколько методов. Рассмотрим решение с помощью метода дифференциальных рент. При нахождении решения...

• ТОЧКА В ОРТОГОНАЛЬНОЙ СИСТЕМЕ ТРЕХ ПЛОСКОСТЕЙ ПРОЕКЦИЙ - Основы моделирования геометрических объектов

  В практике изображения различных геометрических объектов, чтобы сделать проекционный чертеж более ясным, возникает необходимость использовать третью -...

• Показательная функция - Конформное отображение

  Определение 7. Функция вида: называется показательной функцией. Свойства показательных функций: 1) Функция - - дифференцируема во всей плоскости. Так как...

• Векторы, и образуют правую тройку векторов. - Сферический треугольник и его применение

  Свойства: 1. 2. 3. 4. 13. Смешанное произведение векторов и его свойства . Смысл смешенного произведения: сначала два вектора векторно перемножают, а...

• Постановка задачи, Понятие о кубатурных формулах, Метод ячеек - Вычисление кратных интегралов методом ячеек с автоматическим выбором шага

  Найти при помощи метода ячеек значение интеграла , Где - область, ограниченная функциями . 2. Теоретическая часть Рассмотрим K-мерный интеграл вида: (1)...

• Уравнение линии на плоскости - Методы решения системы линейных уравнений

  Как известно, любая точка на плоскости определяется двумя координатами в какой - либо системе координат. Системы координат могут быть различными в...

• ТИПЫ ЗАДАЧ НАЧЕРТАТЕЛЬНОЙ ГЕОМЕТРИИ - Основы моделирования геометрических объектов

  Решение многих задач способами начертательной геометрии, в конечном счете, сводится к определению позиционных и метрических характеристик геометрических...

• Поняття базису. Координати векторів. Єдиність координат. Афінна система координат. Складова й проекція вектора на вісь. Властивості проекцій. Декартова прямокутна система координат - Основи вищої математики

  Визначення : Сукупність лінійно незалежних векторів, по яких відбувається розкладання інших векторів, називається Базисом . Отже, у площині можуть...

• Решение квадратных уравнений, Решение квадратных неравенств, Числовая функция и способы ее задания - Математика в современном мире

  Ответ: уравнение ax2+bx+c=0. Где а не равно нулю, называется квадратным. Чтобы его решить нужно вычислить дискриминант. D=b2 -4ac и сравнить его с нулем....

• Радианная и градусная меры углов, Тригонометрические функции числового аргумента - Действительные числа. Тригонометрические функции числового аргумента. Логарифмы. Частные случаи решения тригонометрических уравнений

  Углом в один градус называется угол равный 1/180 части развернутого угла. Развернутый угол равен 180 градусам. Прямой угол равен половине развернутого...

• Эволюционные механизмы формирования з-областей - Эволюционные процедуры решения комбинаторных задач на графах

  Формирование З -областей в матрице R осуществляется в процессе ее эволюционной модификации. Эволюционная модификация матрицы R производится путем...

• Введение, Основные положения - Эволюционные процедуры решения комбинаторных задач на графах

  Среди набора комбинаторно-логических задач на графах важное место занимает проблема определения паросочетаний, раскраски графа, выделения в графе...

Декартовы прямоугольные координаты, Сферические координаты - Приложение интегрального и дифференциального исчисления к решению прикладных задач

Предыдущая | Следующая