Математическое описание методов нахождения корней уравнения, Метод дихотомии - Исследование функции и ее производной
Метод дихотомии
Этот алгоритм основан на том наблюдении, что график непрерывной функции должен пересечь ось абсцисс между двумя точками a и b как минимум один раз, если значения функции имеют в этих точках разные знаки (рис. 1).
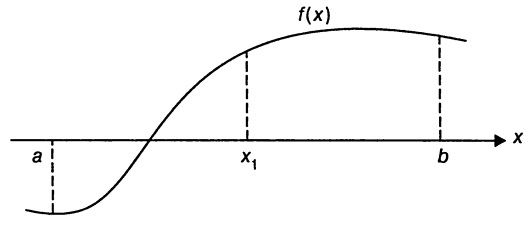
Рисунок 1 - Первая итерация метода дихотомии: x1 - средняя точка отрезка [a, b]
На этом наблюдении, основан алгоритм решения уравнения, называющийся методом дихотомии или методом деления пополам. Начиная с отрезка [a, b] на концах которого f(x) имеет разные знаки, алгоритм вычисляет среднюю точку
Xmid=(a+b)/2.
Если f(xmid)=0, корень найден, и алгоритм завершает работу. В противном случае он продолжает поиск корня либо на отрезке [a, xmid], либо на отрезке [xmid, b] - в зависимости от того, на какой из двух половин отрезка функция f(x) имеет разные знаки на концах нового отрезка.
Поскольку мы не можем ожидать, что алгоритм "наткнется" на точное решение уравнения и завершит работу, нужен иной критерий для его завершения. Можно остановиться, когда отрезок [an, bn], содержащий некоторый корень x*, станет столь мал, что можно гарантировать, что абсолютная ошибка приближения x* величиной xn (средней точкой отрезка) меньше некоторого заранее выбранного значения е>0. Поскольку xn - средняя точка отрезка [an, bn] и x* лежит внутри этого отрезка мы имеем

Следовательно, мы можем завершать работу алгоритма, как только (bn - an)/2<е, или, что то же самое,

Нетрудно доказать, что

Из этого неравенства следует, что последовательность приближений {xn} может быть сделана сколь угодной близкой к x* выбором достаточно большого значения n. Другими словами, мы можем сказать, что {xn} сходится к корню x*.
С помощью неравенства (3) можно заранее определить количество итераций, достаточное для достижения требуемой степени точности. Выбрав n достаточно большим, что бы выполнялось неравенство (b1 - a1)/2n<е, т. е.

,
Мы получим достаточное для обеспечения заданной точности количество итераций.
Основной недостаток метода деления пополам в качестве алгоритма общего назначения для решения уравнений заключается в его низкой скорости сходимости по сравнению с другими известными методами. Кроме того, его нельзя распространить на уравнения более общего вида и на системы уравнений. Однако у этого метода имеются и сильные стороны. Он всегда сходится к корню, каким бы ни был начальный отрезок. Этот метод не использует производную функции f(x), как это делают некоторые более быстрые методы.
Похожие статьи
-
Информатика является основной базой для проведения научно-исследовательских и проектно-технических работ в современной промышленности. С помощью...
-
Исследование математических моделей - Информационные модели
На языке алгебры формальные модели записываются с помощью уравнений, точное решение которых основывается на поиске равносильных преобразований...
-
Описание основных возможностей МКЭ МКЭ представляет собой эффективный метод решения инженерных задач. Область применения метода от анализа напряжений в...
-
В данной работе требуется реализовать программу для решения нелинейного уравнения, иначе говоря найти его корень. Для нахождения корня использован метод...
-
Составление частотного уравнения методом последовательного расщепления Рисунок 3.1 - Исходная модель. Расщепим ее на массе 2 Рисунок 3.2 - Расщепление на...
-
Численные методы. Интерполяция Ньютона
Задание 1 Запишите порядок выполняемых вами операций, оцените погрешности их результатов, вычислите и запишите искомое значение. Определите число верных...
-
Собственными называют периодические колебания консервативной системы, совершающиеся исключительно под воздействием инерционных и упругих сил. Для...
-
Выведем в общем виде уравнение движения заданной динамической модели при помощи уравнений Лагранжа II рода. Полная кинетическая энергия: , Полная...
-
Поиск максимума функции F(x) на отрезке [a;b] - Вычисление максимума функции с некоторыми критериями
Постановка задачи: Необходимо численным методом найти максимум функции F(x)=-L(x1)x2+3.1L(x2)x+5 На отрезке [a;b] с точностью е, при том, что L(x1) и...
-
Метод прямоугольников Пусть требуется определить значение интеграла функции на отрезке. Этот отрезок делится точками на равных отрезков длиной Обозначим...
-
Результаты расчета (точки искомой функции) сохраняются в переменных-массивах: для аргумента X и функции Y, которые отображаются в виде таблицы или...
-
Основная программа Построение интерполяционного многочлена Нахождение максимума функции методом дихотомии Вычисление значения заданной функции Создание и...
-
Описание алгоритма - Решение системы линейных уравнений методом Гаусса
Согласно заданию необходимо разработать программу для решения линейных уравнений методом Гаусса. Поскольку данная программа является приложением Windows,...
-
В работе возникает необходимость выбора предметной области, в которой будет тестироваться каскадный классификатор. Главными вопросами на данном этапе...
-
Методы Рунге-- Кутты-- важное семейство численных алгоритмов решения обыкновенных дифференциальных уравнений и их систем. Данные итеративные методы...
-
2 .1 Постановка задачи Требуется разработать приложение, моделирующее напряженно-деформированное состояние плоской конструкции, провести аналогичный...
-
Средствами решения задачи является алгоритмический язык С++. Операторы и функции, используемые для решения поставленной задачи: #Include - подключение...
-
Программный алгоритм визуальный гаусс В программу включены следующие процедуры: "gauss1", "gaussj", "New1Click", "Button1Click", "Button2Click",...
-
Метод Гаусса. Метод Гаусса решения систем линейных уравнений состоит в последовательном исключении неизвестных и описывается следующей процедурой. С...
-
Онлайн исследования в социологии: новые методы анализа данных - Распространение новостной информации
На сегодняшний день анализ социальных сетей и медиа, Интернет-сообществ, пользователей в целом используется в основном в маркетинге. Компания может...
-
Средствами решения задачи является алгоритмический язык С++. Операторы и функции, используемые для решения поставленной задачи: #Include - подключение...
-
Разработанная программа демонстрирует изученные в процессе обучения навыки владения языком C#. Назначение и условия применения программы Программа...
-
Для дальнейшей работы необходимо построить следующие алгоритмы: алгоритм работы программы в целом, и алгоритм обучения нейросети. Обобщенная схема...
-
В результате курсовой работы можно сделать вывод, что одним из важных этапов технологического проектирования ЭВС является расчет запусков на каждую...
-
Предложенный подход к решению задач исследования Используя в качестве основы присутствующее в наличии программное обеспечение, которое применимо к...
-
Частные производные - Вычисление интегралов в Mathcad
Интегрирование производный компьютерный программа С помощью обоих процессоров MathCAD можно вычислять производные функций любого количества аргументов. В...
-
Постановка задачи Целью работы является изучение основных этапов автоматизированного структурного проектирования технологических маршрутов: -...
-
Для решения сформулированной задачи, т. е, для нахождения оптимального варианта конструкции наиболее эффективным является метод динамического...
-
Конструкция современных электронно-вычислительных средств отличается значительной сложностью и разнообразием. Они представляют собой сложные комплексы,...
-
Описание модулей программы Проект приложения содержит следующие модули. Модуль UnitCollection. pas содержит описание классов для работы с коллекцией и...
-
Численные методы расчета - Алгоритмы компьютерного моделирования
Решить задачу для математической модели - значит указать алгоритм для получения требуемого результата из исходных данных. Алгоритмы решения условно...
-
Постановка задачи Постановка практической задачи ЛП включает следующие основные этапы: - определение показателя эффективности, переменных задачи, -...
-
Метод конечных элементов является численным методом для нахождения приближенных решений физических задач. В основе этого метода лежит разделение...
-
Многие организации, рассматривая вопрос о сетевой безопасности, не уделяют должного внимания методам борьбы с сетевыми атаками на втором уровне. В...
-
Шифрование данных традиционно использовалось спецслужбами и оборонными ведомствами; сейчас, в связи с ростом возможностей компьютерной техники, многие...
-
Комплектной называют поверку, при которой определяются MX СИ, присущие ему как единому целому. Поэлементной называют поверку, при которой значения MX СИ...
-
Геометрический метод, Двойственная задача - Линейное программирование
Применяется для задач с двумя переменными. Метод решения состоит в следующем: На плоскости строятся прямые, которые задают соответствующие ограничения:...
-
Структура комплекса представлена на рисунке 3. Комплекс состоит из следующих модулей: - пользовательский интерфейс; - математическая модель; - библиотека...
-
Основные понятия и определения Прежде чем приступить к обсуждению вопросов оптимизации, введем ряд определений и рассмотрим основные понятия. Оптимизация...
-
Для создания наиболее совершенных и экономичных механизмов и машин важно получить оптимальный вариант входящих в них редукторов (МЗП). Показатель, на...
Математическое описание методов нахождения корней уравнения, Метод дихотомии - Исследование функции и ее производной