Коэффициент детерминации - Математическое описание связи: регрессия, корреляция
Предположим, что экономические предпосылки и анализ расположения точек на корреляционном поле позволил нам выдвинуть гипотезу о том, что зависимость результирующего признака у от фактора х может быть описана следующей моделью:
.
Причем, как не раз мы уже отмечали коэффициенты 0 И 1 в этом уравнении неизвестны. Используя МНК, мы можем найти оценки этих коэффициентов в0 и в1 и записать следующее выражение для у:
.
На приведенном рисунке (Рис.4) изображены фактические значения переменной у, график гипотетической функции регрессии (которая, вообще говоря, нам неизвестна!) и график эмпирической функции регрессии, коэффициенты которой найдены из условия минимума суммы квадратов ошибок.
Рис.4. Графики гипотетической и эмпирической функций регрессии.
Исходя из логики наших действий, возникают два вопроса:
- ?Можно ли с той или иной вероятностью найти подтверждение, что вид функциональной зависимости (речь пока идет только о линейной функции) выбран корректно. ?Насколько хорошо, со статистической точки зрения, оценки неизвестных параметров, полученные по МНК, приближают неизвестные коэффициенты.
Для ответов на поставленные вопросы нам понадобится, в частности, понятие коэффициента детерминации. Перед тем как ввести это понятие рассмотрим следующую сумму:
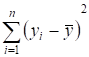
.
Покажем, что ее можно представить в виде:
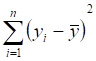
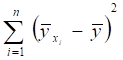
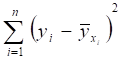
=+.
Действительно,
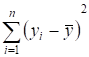
=
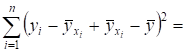
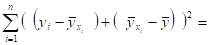
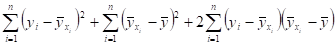
=. (1)

Через обозначена функция регрессии, полученная по МНК: .
Покажем, что последнее слагаемое в (1) равно нулю, для этого запишем его в виде:
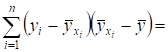
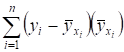
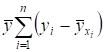
- .
Рассмотрим слагаемое
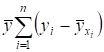
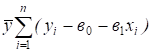
=.
В силу равенства (2), можно утверждать, что оно равно 0. Преобразуем теперь первое слагаемое:
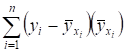
==
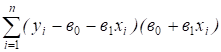
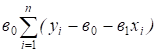
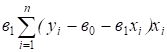
=+.
Оба слагаемых равны нулю в силу равенств (2) и (3).
Таким образом, мы показали, что имеет место, следующее представление для рассматриваемой суммы:
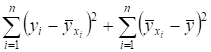
=. (2)
Величину еI равную:
Будем называть остатком. Следовательно, первое слагаемое в правой части (2) есть сумма квадратов остатков:
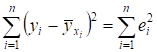
.
Ее называют остаточной суммой квадратов и обозначают RSS (residual sum of squares).
Вторая сумма это сумма квадратов отклонений точек, расположенных на регрессионной прямой от прямой у =. Эту сумму называют суммой квадратов отклонений, объясненной регрессией ЕSS (explained sum of squares).
В левой части равенства (2) находится сумма квадратов отклонений фактических значений переменной у от прямой у =. Такую сумму называют полной суммой квадратов и обозначают TSS (total sum of squares).
Таким образом, полная сумма квадратов TSS разбилась на две составляющие:
TSS= RSS+ ESS. (3)
- ? ESS - сумму квадратов, обусловленных влиянием основного фактора х; ? RSS - сумму квадратов, обусловленных влиянием других, в том числе и случайных факторов.
Замечание 1. Следует иметь в виду, что в литературе по эконометрике, в частности в [9], эту же систему обозначений используют с точностью до наоборот, давая ей другое объяснение. Сумму, которая выше обозначена как ЕSS обозначают через RSS и расшифровывают так: regression sum of squares. И наоборот, сумму, обозначенную нами как RSS называют ЕSS: error sum of squares. Мы будем придерживаться введенной выше терминологии. ^
Замечание 2.Рассмотрим два частных случая. Предположим, что x не оказывает никакого влияния на y, тогда выборочное условное среднее совпадает с выборочным средним, в такой ситуации ЕSS =0 и
TSS= RSS.
В том случае, когда на зависимую переменную у не оказывает влияния никакие другие факторы, кроме х, сумма RSS будет равняться нулю и будет выполняться следующее равенство:
TSS= ESS.
В общем же случае, если оценки параметров функции регрессии найдены по МНК, всегда будет иметь место равенство (3).^
Определение 1. Парным коэффициентом детерминации (выборочным) называют отношение:
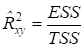
. (4)
Говорят, что "коэффициент детерминации показывает, какая доля дисперсии величины y определяется (детерминируется) изменчивостью (дисперсией) соответствующей функции регрессии y от x" [1].
Поясним сказанное. Для этого вернемся к равенству (2) и разделим обе части равенства на n, получим:
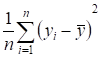
=.
Или:
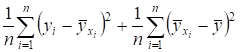
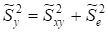
.
Тогда выражение для парного коэффициента детерминации можно представить в виде:
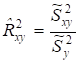
. (5)
Следует отметить, что введенный нами парный коэффициент детерминации также относится к выборочным числовым характеристикам и рассчитывается по эмпирическим данным. Теоретический коэффициент детерминации будем обозначать RXy.
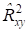
Рассмотрим, в каком диапазоне изменяется значение коэффициента детерминации. Очевидно, что эта величина всегда неотрицательна. Найдем верхнюю границу. Из равенства (3) следует следующее равенство:
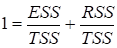
.
Следовательно,
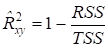
.
Отсюда очевидно, что в силу того, что наименьшее значение RSS =0, наибольшее значение коэффициента детерминации равно 1. Таким образом,
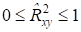
.
Отметим, что значение коэффициента детерминации тем ближе к 1, чем меньше остаточная сумма квадратов. В этом случае говорят, что уравнение регрессии статистически значимо и фактор х оказывает сильное воздействие на результирующий признак у (последний тезис справедлив только для модели парной линейной регрессии!).
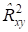
Покажем, как связаны коэффициент парной детерминации с выборочным коэффициентом корреляции, чтобы аргументировать последнее утверждение.
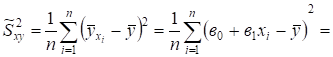
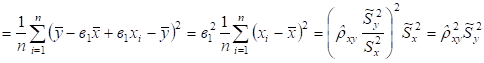
.
Подставим это выражение в числитель формулы (5):
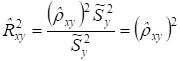
.
Следовательно, в случае парной линейной регрессии, коэффициент детерминации равен квадрату выборочного коэффициента корреляции:
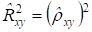
. (6)
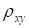
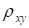
Замечание 1. Из теории вероятностей известно следующее свойство коэффициента корреляции. Коэффициент корреляции двух случайных величин равен 1 или -1 тогда и только тогда, когда случайные величины связаны между собой линейно, т. е. у = ах + в. Классификация силы связи двух случайных величин в зависимости от величины коэффициента корреляции (теоретического!) может производиться следующим образом.
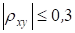
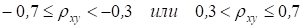
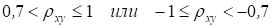
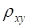
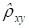
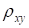
Если то связь между случайными величинами классифицируют как слабую; если то силу связи между двумя случайными величинами классифицируют как среднюю и, наконец, если, то говорят, что имеет место сильная стохастическая зависимость. Причем, если коэффициент корреляции положительный, то связь классифицируют как прямую, то есть значение обеих случайных величин увеличиваются, или уменьшаются одновременно. Отрицательное значение коэффициента корреляции говорит об обратной связи, то есть, например, увеличение значений одной случайной величины ведет к уменьшению значений другой. Следует иметь в виду, что использование выборочного коэффициента корреляции для подобной классификации, требует вдумчивого подхода. Эта характеристика является по своей сути случайной величиной и нельзя по ее значению делать категоричные выводы, подобные тем, которые производят, ориентируясь на. Все суждения, должны носить уже в этом случае более осторожный характер.
Тем не менее, и выборочный коэффициент корреляции и парный коэффициент детерминации служат хорошим индикатором, позволяющим нам делать предположение о том, что зависимость между х и у имеет место, и она носит вид линейной функциональной зависимости.
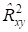
Вернемся к парному коэффициенту детерминации. Если модуль выборочного коэффициента корреляции близок к 1, то из формулы (6) следует, что близок к 1 и. Таким образом, близость коэффициента детерминации или абсолютной величины выборочного коэффициента корреляции к 1, служит еще одним основанием в поддержку предположения, что функция регрессии линейна.
При анализе модели парной линейной регрессии будем делать следующие предварительные выводы о качестве модели.
- ?Если [0; 0,09], то будем считать, что использование регрессионной модели для аппроксимации зависимости между у и х статистически необоснованно. ?Если (0,09; 0,49], то использование регрессионной модели возможно, но после оценивания параметров, модель подлежит дальнейшему многостороннему статистическому анализу. ?Если (0,49; 1], то будем считать, что у нас есть основания для использования регрессионной модели, при анализе поведения переменной у.
Пример 1. Вычислим коэффициент детерминации и сделаем предварительный вывод о качестве аппроксимации доходности акций компании Glenwood City Properties моделью линейной регрессии (пример 1).
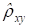
Решение. Так как значение выборочного коэффициента корреляции нам уже известно, то для нахождения воспользуемся формулой (6):
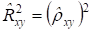
=(0,593595)2.
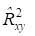
И значение, и значение, говорят о слабой зависимости между доходностью рыночного индекса и доходностью акций указанной компании. Такая слабая зависимость обычно характерна для компаний с низкой рыночной капитализацией, которые не участвуют в формировании рыночного индекса. ^
Так, например, индекс S&;P 500 (Standard &; Poors Stock Price Index) представляет средневзвешенную величину курсов акций 500 наиболее крупных компаний. Наиболее часто цитируемым рыночным индексом является индекс Доу Джонса (DJIA), основанный на показателях всего 30 акций. Впервые этот индекс был вычислен в 1884 как среднеарифметическое 11 акций, с 1928 для расчета индекса используется 30 ценных бумаг. Состав бумаг, входящих в индекс, периодически меняется.
Похожие статьи
-
В эконометрике приходится сталкиваться с двумя ситуациями. Уже имеющаяся математическая модель, построенная, исходя из тех или иных экономических...
-
Модель парной линейной регрессии - Математическое описание связи: регрессия, корреляция
Предположим, что у нас есть все основания считать, что два экономических показателя взаимосвязаны. Например, уровень инфляции и уровень безработицы в...
-
Использование в экономических исследованиях методов регрессии и корреляции - Эконометрика как наука
Начальным пунктом эконометрического анализа зависимостей обычно является оценка линейной зависимости переменных. Это объясняется простотой исследования...
-
Множественная регрессия - уравнение связи с несколькими независимыми переменными: где - зависимая переменная (результативный признак); - независимые...
-
Применим аппарат. Результаты приведены ниже Таблица 6. индексный анализ Рисунок 4. График сглаженного признака Полиномиальная регрессия Приведем массив...
-
Корреляция и регрессия Вспомним, что зависимости называются вероятностными или стохастическими, если каждому набору факторов Х I соответствует множество...
-
Коэффициент корреляции - Основы научных исследований
Если между случайными величинами Х и У существует линейная корреляционная зависимость (рис. 12.5 а, б,г), то интенсивность корреляционной связи...
-
Признаки Х и Y находятся в Корреляционной зависимости , если каждому значению одного признака X I соответствует определенная Условная средняя другого...
-
Тадии парного регрессионного анализа можно представить на следующем рисунке ПОЛЕ КОРРЕЛЯЦИИ Это графическое изображение точек с координатами, которые...
-
Причинность, регрессия, корреляция Исследование объективно существующих зависимостей и взаимосвязей между явлениями и процессами - важнейшая задача...
-
В состав системы эконометрических уравнений входят множество зависимых или эндогенных переменных и множество предопределенных переменных (лаговые и...
-
Управление с обратной связью, Программное управление - Математическое описание объектов управления
Всегда, когда имеется информация о состоянии объекта, о результатах управления ее следует использовать для повышения качества управления. В рассмотренной...
-
Литература - Математическое описание связи: регрессия, корреляция
1. Айвазян С. А., Енюков И. С., Мешалкин Л. Д. Прикладная статистика. Исследование зависимостей. - М.: Финансы и статистика, 1985. 2. Березинец И. В....
-
Математическим ожиданием случайной величины х (М[x])называется средне взвешенно значение случайной величины причем в качестве весов выступают вероятности...
-
Собственно-корреляционные параметрические методы изучения связи - Основы эконометрики
Измерение тесноты и направления связи является важной задачей изучения и количественного измерения взаимосвязи социально-экономических явлений. Оценка...
-
В большинстве случаев 0 и 1 неизвестны. Их определяют (оценивают), исходя из имеющихся выборочных наблюдений с помощью следующего уравнения: Где -...
-
Составляется матрица численных значений базисных функций, соответствующая расширенной матрице спектра плана Вычисляется информационная матрица...
-
Множественный коэффициент корреляции - Основы научных исследований
Задача определения интенсивности или, как ее еще называют, тесноты связи между более чем двумя переменными относится к множественному корреляционному...
-
Парная линейная регрессия и корреляция
Парная линейная регрессия и корреляция Задание 1 По имеющимся данным (таблица 1) изучите зависимость прибыли от выработки продукции на одного человека,...
-
1. Определение параметров модели парной линейной регрессии методом наименьших квадратов 2. Оценка тесноты связи между переменными 3. Оценка качества...
-
Простая линейная регрессия - Моделирование в эконометрике
Простой регрессией называется односторонняя стохастическая зависимость результативной переменной только от одной объясняющей переменной: Простая линейная...
-
Важной задачей статистики является разработка методики статистической оценки социально-экономических явлений, которая осложняется тем, что многие...
-
В основе метода площадей лежит предположение, что объект может быть описан линейным дифференциальным уравнением с постоянными коэффициентами, а его...
-
На следующем этапе в модель были добавлены дамми-переменные годов и отраслей. Таблицы соотношения переменных и данных приведены ниже. Кроме дамми...
-
По данным динамики валют (вариант 14) выявить трендовую, периодическую и случайную составляющие ряда (T, S,E), оценить качество модели, сделать прогноз...
-
ЧАСТНАЯ КОРРЕЛЯЦИЯ - Многомерный статистический анализ
Мы установили, что линейный коэффициент корреляции - это показатель силы связи, описывающий линейную зависимость между двумя переменными. Тогда частный...
-
Имеется выборка объема n экспериментальных значений. Предполагаем, что ошибки вычисления пренебрежимо малы, а случайные ошибки измерения температур...
-
Парная нелинейная регрессия - Статистическое изучение взаимосвязи социально-экономических явлений
Наиболее часто при описании взаимосвязи социально-экономических явлений, кроме линейной модели, используют следующие виды зависимостей: Гиперболическая ;...
-
Экономический корреляционный регрессионный Парная линейная регрессия Парная регрессия характеризует связь между двумя признаками: результативным и...
-
Прогностическая сила - Базовые результаты математической теории классификации
С целью поиска приемлемого показателя качества диагностики рассмотрим восходящую к Р. Фишеру [20] широко известную параметрическую вероятностную модель...
-
Описание используемых методов - Моделирование вероятности банкротства
В данной работе было принято решение использовать логистический анализ с помощью пакета STATA, а также алгоритм CART с помощью SPSS Modeler. Бинарная...
-
Задача регрессии. Метод наименьших квадратов Ищу функцию регрессии в виде (1*). Оценки коэффициентов нахожу с помощью Метода Наименьших Квадратов (МКВ),...
-
Парная регрессия на основе метода наименьших квадратов и метода группировок - Основы эконометрики
Парная регрессия Характеризует связь между двумя признаками: результативным и факторным. Аналитически связь между ними описывается уравнениями: Прямой...
-
Множественная линейная регрессия
Задание Линейный регрессия переменная детерминация Составить уравнение линейной регрессии, используя МНК, и найти числовые характеристики переменных....
-
Нелинейные модели регрессии - Моделирование в эконометрике
Нелинейные модели регрессии и их линеаризация. 1. Типы нелинейных моделей: 2. Нелинейные модели линейные по объясняющим переменным и их линеаризация. 3....
-
Выбор математической формы функции при моделировании зависимости выпуска продукции от производственных факторов Постановка проблемы. Одним из важнейших...
-
Множественная регрессия - Эконометрика как наука
Общее назначение множественной регрессии (этот термин был впервые использован в работе Пирсона - Pearson, 1908) состоит в анализе связи между несколькими...
-
Описание модели Экономические агенты, участвующее в модели: 1) производство 2) население 3) центральный банк 4) администрация региона Создадим...
-
Коэффициент частной корреляции - Основы научных исследований
Показывает интенсивность связи между двумя переменными при фиксировании или исключении влияния остальных переменных. Пусть имеет место множественная...
-
Постоянство механизмов. Одно из условий, на которое опирается эконометрическое моделирование, состоит в том, что функциональное соотношение не меняется в...
Коэффициент детерминации - Математическое описание связи: регрессия, корреляция