Модель множественной линейной регрессии, Линейная множественная регрессия - Моделирование в эконометрике
- 1. Определение параметров модели парной линейной регрессии методом наименьших квадратов 2. Оценка тесноты связи между переменными 3. Оценка качества уравнения регрессии 4. Предпосылки метода наименьших квадратов
Линейная множественная регрессия
В действительности каждое явление определяется действием не одной причины, а нескольких, а точнее целым комплексом причин. Сложное сочетание причин приводит к различным результатам. Например, действуя в одном и том же направлении, они усиливают действие, действуя в противоположном направлении - ослабляют друг друга. Возникает вопрос об измерении воздействия комплекса причин на изучаемое явление. Задача изучения зависимости одной зависимой переменной от нескольких объясняющих переменных X1, X2, ..., XM в условиях конкретного времени решается с помощью множественного или многофакторного регрессионного анализа. Рассмотрим линейное соотношение между переменной Y и объясняющими переменными X1, X2, ..., XM.
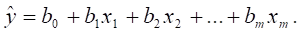
Коэффициенты BK, k = 0, 1, 2, ..., m называются параметрами регрессии. Постоянная регрессии B0 выполняет в уравнении регрессии функцию выравнивания. Она определяет точку пересечения гиперповерхности регрессии с осью Y. Значения B1, B2, ..., BM являются оценками коэффициентов регрессии. Коэффициент регрессии BK измеряет усредненное частное влияние изменения переменной XK, k = 1, 2, ..., m, в предположении, что остальные объясняющие переменные (x1, X2, ..., XK-1, XK+1, ..., XM) остаются без изменения на постоянном уровне. Поэтому с точки зрения статистической методологии нет различия между множественной и частной регрессией. По этой причине в литературе параметры BK, k = 1, 2, ..., m называются как коэффициентами множественной, так и частной регрессии. Но заключение о том, что для определения коэффициентов регрессии достаточно определить несколько простых линейных регрессий Y на XK, k = 1, 2, ..., m является ошибочным. Для достоверных оценок нужны методы оценивания, учитывающие многосторонние связи совместно зависимых переменных. Наиболее часто используют двухшаговый метод наименьших квадратов, который является обобщением метода наименьших квадратов.
Рассмотрим сначала линейную множественную регрессию с двумя объясняющими переменными:
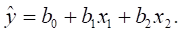
Метод наименьших квадратов приводит к условию:
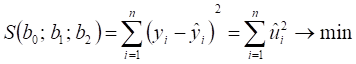
, откуда
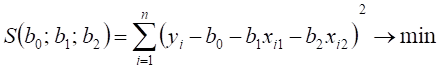
После дифференцирования S(b0, B1, B2) по каждому из параметров B0, B1, B2 и приравнивания к нулю всех частных производных функции S(b0, B1, B2) по каждому из параметров B0, B1, B2, получаем следующую систему нормальных уравнений:
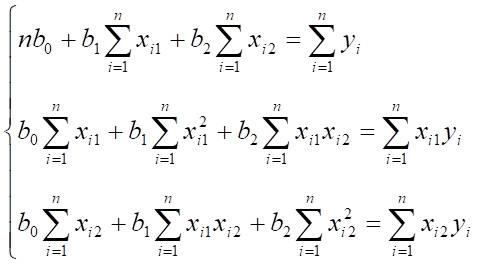
Решить полученную систему нормальных уравнений относительно неизвестных параметров можно по формулам Крамера.
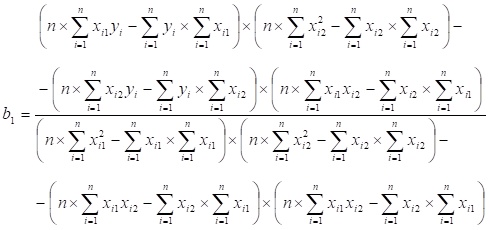
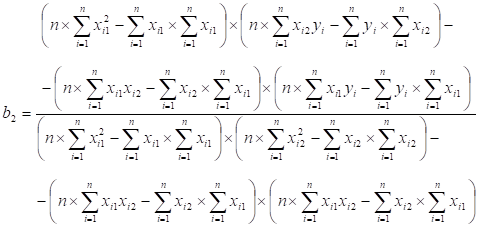
Коэффициенты множественной или частной регрессии можно представить через дисперсии и ковариации:
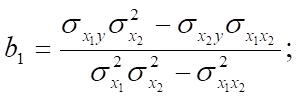
Где
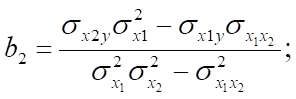
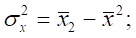
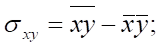
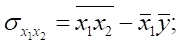
Пример
Построим линейную множественную регрессию общей суммы налогов и платежей на общую сумму поступлений по налогу на добавленную стоимость и налогу на прибыль (доход).
|
Время наблюдения |
Y (общая сумма налогов и платежей в консолидированный бюджет РФ), млрд. руб. |
X1 (общая сумма поступлений в консолидированный бюджет РФ по налогу на прибыль), млрд. руб. |
X2 (общая сумма поступлений в консолидированный бюджет РФ по НДС), млрд. руб. |
|
Январь |
38,9 |
5,6 |
13,4 |
|
Февраль |
45,3 |
6,7 |
15,4 |
|
Март |
61,1 |
13,1 |
16,7 |
|
I квартал |
145,3 |
25,3 |
45,5 |
|
Апрель |
70,4 |
16,9 |
16,2 |
|
Май |
63,8 |
18,4 |
13 |
|
Июнь |
67,7 |
19,1 |
15 |
|
II квартал |
201,9 |
54,4 |
44,2 |
|
I полугодие |
347,2 |
79,8 |
89,7 |
|
Июль |
70,6 |
16,1 |
20,8 |
|
Август |
78,9 |
23,3 |
16,4 |
|
Сентябрь |
73,2 |
19,2 |
17,4 |
|
III квартал |
222,7 |
58,6 |
54,6 |
|
9 месяцев |
569,9 |
138,3 |
144,3 |
|
Октябрь |
78,1 |
16,1 |
23,6 |
|
Ноябрь |
103 |
31,8 |
23,9 |
|
Декабрь |
133,4 |
35,4 |
34,4 |
|
IV квартал |
314,5 |
83,3 |
81,9 |
|
II полугодие |
537,2 |
141,9 |
136,5 |
|
Январь-декабрь |
884,4 |
221,6 |
226,1 |
|
Уy |
Уx1 |
Уx2 |
Уx1y |
Уx2y |
Уx12 |
Уx22 |
Уx1X2 |
|
884,4 |
221,6 |
226,1 |
18614,15 |
18154,57 |
4931,19 |
4667,94 |
4605,29 |
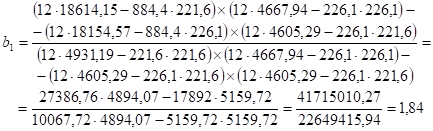
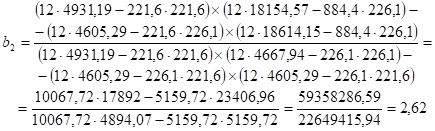
Полученные значения B1 и B2 подставим в уравнение
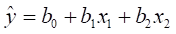
И выразим B0.
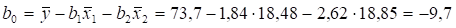
Для описания линейной множественной регрессии с количеством объясняющих переменных больше двух будем использовать матричное исчисление. Пусть
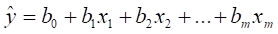
, или
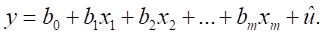
Введем фиктивную переменную X0 полагая XI0 = 1, i=1, 2, ..., n.
Положим
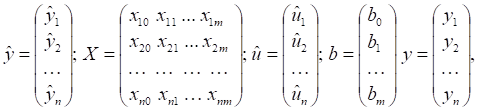
Где XIj - переменная для обозначения переменной XJ при наблюдении I, J = 1, 2, ..., M; I = 1, 2, ..., N.
Тогда уравнение регрессии запишется следующим образом:
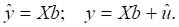
Применяя метод наименьших квадратов, получим:
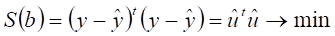
,
Где АT - матрица, транспонированная к А. Подставляя вместо y в последнюю формулу Xb, получаем
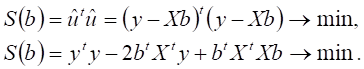
Дифференцируя последнее выражение по B и приравнивая его к нулю, получаем:
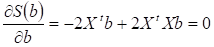
Нормальное уравнение имеет следующий вид:
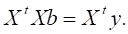
Если матрица XTX обратима, то
Похожие статьи
-
Множественная регрессия - уравнение связи с несколькими независимыми переменными: где - зависимая переменная (результативный признак); - независимые...
-
Линейная модель парной регрессии - Моделирование в эконометрике
Введение в регрессионный анализ. Модель парной линейной регрессии. 1. Метод наименьших квадратов (МНК). 2. Свойства оценок МНК 3. Модель парной линейной...
-
Нелинейные модели регрессии - Моделирование в эконометрике
Нелинейные модели регрессии и их линеаризация. 1. Типы нелинейных моделей: 2. Нелинейные модели линейные по объясняющим переменным и их линеаризация. 3....
-
Простая линейная регрессия - Моделирование в эконометрике
Простой регрессией называется односторонняя стохастическая зависимость результативной переменной только от одной объясняющей переменной: Простая линейная...
-
Множественная линейная регрессия
Задание Линейный регрессия переменная детерминация Составить уравнение линейной регрессии, используя МНК, и найти числовые характеристики переменных....
-
Коэффициенты структурной модели могут быть оценены разными способами в зависимости от вида системы одновременных уравнений. Наибольшее распространение...
-
Фиктивные переменные во множественной регрессии - Моделирование в эконометрике
До сих пор в качестве факторов рассматривались экономические переменные, принимающие количественные значения в некотором интервале. Вместе с тем может...
-
1. Предпосылки метода наименьших квадратов. 2. Проблема мультиколлинеарности. 3. Гомоскедатичность и гетероскедатичность. Линейные регрессионные модели с...
-
Структурная и приведенная формы модели. - Моделирование в эконометрике
Система совместных, одновременных уравнений (или структурная форма модели) обычно содержит эндогенные и экзогенные переменные. Эндогенные Переменные...
-
Вопросы: 1. Общее понятие о системах одновременных уравнений. 2. Структурная и приведенная формы модели. 3. Проблема идентификации. 4. Оценивание...
-
Обобщенный метод наименьших квадратов - Моделирование в эконометрике
При наличии гетероскедастичности в остатках рекомендуется традиционный метод наименьших квадратов (МНК) заменять обобщенным методом наименьших квадратов...
-
Будем моделировать среднегодовую численность занятого населения с помощью показателей общей численности населения и миграционного прироста Среднегодовая...
-
Методы наименьших квадратов - Системы эконометрических уравнений, их применение в эконометрике
Как уже отмечалось, разработана масса методов эвристического анализа систем эконометрических уравнений. Они предназначены для решения тех или иных...
-
Основные этапы построения эконометрической модели - Моделирование в эконометрике
Построение эконометрической модели является основой эконометрического исследования. Оно основывается на предположении о реально существующей зависимости...
-
Модели вида, Зависимость - Моделирование в эконометрике
Называются полулогарифмическими моделями. Эти модели также относятся к нелинейным моделям относительно включенных в анализ объясняющих переменных, но...
-
Построение модели с помощью логистической регрессии Прежде чем строить логистическую регрессию, необходимо выбрать конечный набор финансовых и...
-
Модель парной линейной регрессии - Математическое описание связи: регрессия, корреляция
Предположим, что у нас есть все основания считать, что два экономических показателя взаимосвязаны. Например, уровень инфляции и уровень безработицы в...
-
Построим показательный тренд ВВП. Используем данные таблицы (в млрд. руб) [14]. Таблица 1. Данные к работе Год Квартал Номер квартала ВВП 2001 I 1 1900,9...
-
Возьмем данные об инвестициях в основной капитал (млрд. руб.) Год Квартал Номер квартала Значение 2003 I 1 330 II 2 470,4 III 3 608,8 IV 4 773,7 2004 I 5...
-
В эконометрике приходится сталкиваться с двумя ситуациями. Уже имеющаяся математическая модель, построенная, исходя из тех или иных экономических...
-
Парная линейная регрессия и корреляция
Парная линейная регрессия и корреляция Задание 1 По имеющимся данным (таблица 1) изучите зависимость прибыли от выработки продукции на одного человека,...
-
Тадии парного регрессионного анализа можно представить на следующем рисунке ПОЛЕ КОРРЕЛЯЦИИ Это графическое изображение точек с координатами, которые...
-
Экономический корреляционный регрессионный Парная линейная регрессия Парная регрессия характеризует связь между двумя признаками: результативным и...
-
Постоянство механизмов. Одно из условий, на которое опирается эконометрическое моделирование, состоит в том, что функциональное соотношение не меняется в...
-
Вычисляют выборочную дисперсию, характеризующую меру разброса опытных данных (x I ; Y I ) вокруг значений регрессии, то есть дисперсию остатков ....
-
Множественная регрессия - Эконометрика как наука
Общее назначение множественной регрессии (этот термин был впервые использован в работе Пирсона - Pearson, 1908) состоит в анализе связи между несколькими...
-
Построение линейного уравнения парной регрессии
Задача Таблица 1 Номер региона Среднедушевой прожиточный минимум в день одного трудоспособного, руб., Среднедневная заработная плата, руб., 1 78 133 2 82...
-
Проблема идентификации. - Моделирование в эконометрике
При переходе от приведенной к структурной форме модели возникает проблема идентификации. Идентификация - это единственность соответствия между...
-
Примеры лаговых моделей в экономике - Экономическое моделирование временных рядов
Модель адаптивных ожиданий Моделью адаптивных ожиданий называется динамическая эконометрическая модель, которая учитывает предполагаемое (или желаемое)...
-
Уравнение динамики теплообменника: Передаточные функции объекта получим по его уравнению динамики. Для этого запишем уравнение по заданному каналу. Затем...
-
Гомоскедастичность, Отсутствие автокорреляции остатков - Моделирование в эконометрике
Гомоскедастичность остатков означает, что дисперсия каждого отклонения одинакова для всех значений X . Если это условие не соблюдается, то имеет место...
-
В состав системы эконометрических уравнений входят множество зависимых или эндогенных переменных и множество предопределенных переменных (лаговые и...
-
Методы оценки параметров структурной формы модели - Основы эконометрики
Коэффициенты структурной модели могут быть оценены разными способами в зависимости от вида системы одновременных уравнений. Наибольшее распространение в...
-
Парная регрессия на основе метода наименьших квадратов и метода группировок - Основы эконометрики
Парная регрессия Характеризует связь между двумя признаками: результативным и факторным. Аналитически связь между ними описывается уравнениями: Прямой...
-
Метод частных средних - Моделирование в эконометрике
Среднее, связанное с определенными предположениями или вычисленное при определенных условиях, называется частным, условным или групповым средним. Частные...
-
Аналитическое выравнивание временного ряда. - Моделирование в эконометрике
Рассмотрим модель временного ряда yT = F (t) + , где F (t) - неслучайная составляющая (тренд, либо тренд и циклическая и (или) сезонная компонента,...
-
В основе метода площадей лежит предположение, что объект может быть описан линейным дифференциальным уравнением с постоянными коэффициентами, а его...
-
Имеется выборка объема n экспериментальных значений. Предполагаем, что ошибки вычисления пренебрежимо малы, а случайные ошибки измерения температур...
-
Необходимо составить математическое описание теплообменника, в котором жидкий продукт нагревается насыщенным водяным паром (расход, кг/с), до температуры...
-
Эконометрические методы могут быть применены в моделировании, имитации и прогнозировании рыночных процессов. Достаточно широко в маркетинге используются...
Модель множественной линейной регрессии, Линейная множественная регрессия - Моделирование в эконометрике