Решение систем линейных уравнений
Постановка задачи
Решить Систему линейных уравнений при помощи метода Гаусса и через метод Крамера (вариант 82- 2)
Теоретическая часть
Матрица -- Таблица чисел, содержащая m строк и n столбцов. Числа (m, n) называются порядком, или размером матрицы. Если m=n, то матрица называется квадратной матрицей порядка n. Пример квадратной матрицы 3 порядка:
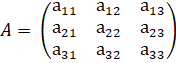
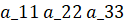
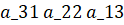
Ячейки называются главной диагональю матрицы, а ячейки называются ее побочной диагональю. Матрицы A и B называются равными, если имеют одинаковые порядки, и соответствующие элементы этих матриц равны, то есть A=B, если.
Определитель Матрицы -- число, соответствующее квадратной матрице, полученное путем ее преобразования по определенному правилу. Обозначается как Det A. Вычисляется следующим образом ( на примере квадратной матрицы 2-го порядка)
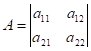
; Det A=a11A22 - a12A21.
В общем случае (для квадратной матрицы порядка N) из элементов матрицы A сначала составляют все возможные произведения из N сомножителей каждое, содержащие по одному элементу из каждой строки и по одному элементу из каждого столбца, затем эти произведения складываются по определенному правилу.
Определитель матрицы, в которой вычеркнуты произвольная строка (напр. I-я), и произвольный столбец (напр. J-й), называется минором. Он имеет (N - 1)-й порядок, т. е. порядок на 1 меньше, нежели исходный определитель
Метод Гаусса - это метод последовательного исключения переменных, когда с помощью элементарных преобразований система уравнений приводится к равносильной системе ступенчатого вида, из которого последовательно, начиная с последних (по номеру) переменных, находятся все остальные переменные.
Пусть исходная система выглядит так:
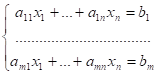
Представим ее в виде матриц:
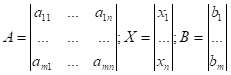
С помощью элементарных преобразований матрицу A можно привести к диагональному виду.
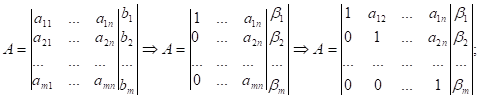
Обратный ход метода Гаусса:
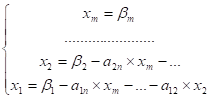
Метод Крамера (Правило Крамера) -- способ решения квадратных систем линейных алгебраических уравнений с ненулевым определителем основной матрицы (причем для таких уравнений решение существует и единственно). матрица линейный уравнение гаусс
Для системы N линейных уравнений с N неизвестными:
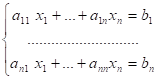
С определителем матрицы системы ?, отличным от нуля, решение записывается в виде:
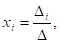
где
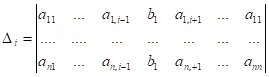
(I-й столбец матрицы системы заменяется столбцом свободных членов)
Практическая часть
I. Конкретная система линейных уравнений
Решение системы линейных уравнений методом Гаусса
Представим систему линейных уравнений в виде матрицы:
|
12 |
4,7 |
-1,7 |
-1,9 |
0 |
-6,1 |
8,8 |
-13 |
-25 |
|
2,4 |
-8,3 |
1,6 |
12 |
10 |
5 |
6,3 |
-10 |
1 |
|
9,6 |
0 |
-7,1 |
-5 |
-0,49 |
-6,9 |
-9,9 |
0,43 |
-14 |
|
12 |
-7,3 |
-4,9 |
-11 |
-5,7 |
-9,8 |
-10 |
0 |
-25 |
|
-4,3 |
-3,7 |
14 |
-7,9 |
7,8 |
0 |
6,1 |
4,8 |
-5,9 |
|
-8,7 |
5,6 |
14 |
-5,5 |
0,41 |
-11 |
3,8 |
2,3 |
-30 |
|
6,1 |
3,9 |
7,4 |
3,2 |
-13 |
-11 |
0,4 |
11 |
-23 |
|
1,8 |
-11 |
-0,95 |
-7,9 |
-10 |
12 |
6 |
0 |
36 |
Поделим первую строку на 12, и далее, умножив первую строку на -2,4 складываем со второй строкой, умножив на -9,6 с третьей, на -12 с четвертой, на 4,3 с пятой, на 8,7 с шестой, на -6,1 с седьмой, на -1,8 с восьмой. Получаем:
|
1 |
0,39166667 |
-0,14167 |
-0,15833 |
0 |
-0,50833 |
0,733333 |
-1,08333 |
-2,08333 |
|
0 |
-9,24 |
1,94 |
12,38 |
10 |
6,22 |
4,54 |
-7,4 |
6 |
|
0 |
-3,76 |
-5,74 |
-3,48 |
-0,49 |
-2,02 |
-16,94 |
10,83 |
6 |
|
0 |
-12 |
-3,2 |
-9,1 |
-5,7 |
-3,7 |
-18,8 |
13 |
0 |
|
0 |
-2,01583333 |
13,39083 |
-8,58083 |
7,8 |
-2,18583 |
9,253333 |
0,141667 |
-14,8583 |
|
0 |
9,0075 |
12,7675 |
-6,8775 |
0,41 |
-15,4225 |
10,18 |
-7,125 |
-48,125 |
|
0 |
1,51083333 |
8,264167 |
4,165833 |
-13 |
-7,89917 |
-4,07333 |
17,60833 |
-10,2917 |
|
0 |
-11,705 |
-0,695 |
-7,615 |
-10 |
12,915 |
4,68 |
1,95 |
39,75 |
Поделим вторую строку на 9,24, и далее, умножив вторую строку на 3,76 складываем с третьей строкой, умножив на 12 с четвертой, на 2,01583333 с пятой, на -9,0075 с шестой, на -1,51083333 с седьмой, на 11,705 с восьмой.
Получаем новую матрицу:
|
1 |
0,39166667 |
-0,14167 |
-0,15833 |
0 |
-0,50833 |
0,733333 |
-1,08333 |
-2,08333 |
|
0 |
1 |
-0,20996 |
-1,33983 |
-1,08225 |
-0,67316 |
-0,49134 |
0,800866 |
-0,64935 |
|
0 |
0 |
-6,52944 |
-8,51775 |
-4,55926 |
-4,55108 |
-18,7874 |
13,84126 |
3,558442 |
|
0 |
0 |
-5,71948 |
-25,1779 |
-18,687 |
-11,7779 |
-24,6961 |
22,61039 |
-7,79221 |
|
0 |
0 |
12,9676 |
-11,2817 |
5,618362 |
-3,54281 |
8,26287 |
1,756079 |
-16,1673 |
|
0 |
0 |
14,65869 |
5,19099 |
10,15838 |
-9,35901 |
14,60576 |
-14,3388 |
-42,276 |
|
0 |
0 |
8,581376 |
6,190088 |
-11,3649 |
-6,88213 |
-3,331 |
16,39836 |
-9,31061 |
|
0 |
0 |
-3,15254 |
-23,2977 |
-22,6677 |
5,03566 |
-1,07116 |
11,32413 |
32,14935 |
Далее по аналогии:
|
1 |
0,39166667 |
-0,14167 |
-0,15833 |
0 |
-0,50833 |
0,733333 |
-1,08333 |
-2,08333 |
|
0 |
1 |
-0,20996 |
-1,33983 |
-1,08225 |
-0,67316 |
-0,49134 |
0,800866 |
-0,64935 |
|
0 |
0 |
1 |
1,304515 |
0,698263 |
0,69701 |
2,877345 |
-2,11982 |
-0,54498 |
|
0 |
0 |
0 |
-17,7168 |
-14,6933 |
-7,79139 |
-8,23918 |
10,4861 |
-10,9092 |
|
0 |
0 |
0 |
-28,1981 |
-3,43643 |
-12,5814 |
-29,0494 |
29,24509 |
-9,10018 |
|
0 |
0 |
0 |
-13,9315 |
-0,07724 |
-19,5763 |
-27,5723 |
16,73503 |
-34,2872 |
|
0 |
0 |
0 |
-5,00445 |
-17,357 |
-12,8634 |
-28,0226 |
34,58936 |
-4,63389 |
|
0 |
0 |
0 |
-19,1851 |
-20,4664 |
7,233014 |
7,999798 |
4,641298 |
30,43126 |
|
1 |
0,39166667 |
-0,14167 |
-0,15833 |
0 |
-0,50833 |
0,733333 |
-1,08333 |
-2,08333 |
|
0 |
1 |
-0,20996 |
-1,33983 |
-1,08225 |
-0,67316 |
-0,49134 |
0,800866 |
-0,64935 |
|
0 |
0 |
1 |
1,304515 |
0,698263 |
0,69701 |
2,877345 |
-2,11982 |
-0,54498 |
|
0 |
0 |
0 |
1 |
0,829345 |
0,439775 |
0,46505 |
-0,59187 |
0,615757 |
|
0 |
0 |
0 |
0 |
19,94953 |
-0,18053 |
-15,9358 |
12,55536 |
8,263027 |
|
0 |
0 |
0 |
0 |
11,47676 |
-13,4495 |
-21,0935 |
8,489344 |
-25,7088 |
|
0 |
0 |
0 |
0 |
-13,2065 |
-10,6626 |
-25,6953 |
31,62736 |
-1,55236 |
|
0 |
0 |
0 |
0 |
-4,55536 |
15,67015 |
16,92184 |
-6,71388 |
42,24465 |
|
1 |
0,39166667 |
-0,14167 |
-0,15833 |
0 |
-0,50833 |
0,733333 |
-1,08333 |
-2,08333 |
|
0 |
1 |
-0,20996 |
-1,33983 |
-1,08225 |
-0,67316 |
-0,49134 |
0,800866 |
-0,64935 |
|
0 |
0 |
1 |
1,304515 |
0,698263 |
0,69701 |
2,877345 |
-2,11982 |
-0,54498 |
|
0 |
0 |
0 |
1 |
0,829345 |
0,439775 |
0,46505 |
-0,59187 |
0,615757 |
|
0 |
0 |
0 |
0 |
1 |
-0,00905 |
-0,79881 |
0,629356 |
0,414196 |
|
0 |
0 |
0 |
0 |
0 |
-13,3457 |
-11,9258 |
1,266377 |
-30,4624 |
|
0 |
0 |
0 |
0 |
0 |
-10,7821 |
-36,2448 |
39,93898 |
3,91774 |
|
0 |
0 |
0 |
0 |
0 |
15,62892 |
13,28299 |
-3,84694 |
44,13147 |
|
1 |
0,39166667 |
-0,14167 |
-0,15833 |
0 |
-0,50833 |
0,733333 |
-1,08333 |
-2,08333 |
|
0 |
1 |
-0,20996 |
-1,33983 |
-1,08225 |
-0,67316 |
-0,49134 |
0,800866 |
-0,64935 |
|
0 |
0 |
1 |
1,304515 |
0,698263 |
0,69701 |
2,877345 |
-2,11982 |
-0,54498 |
|
0 |
0 |
0 |
1 |
0,829345 |
0,439775 |
0,46505 |
-0,59187 |
0,615757 |
|
0 |
0 |
0 |
0 |
1 |
-0,00905 |
-0,79881 |
0,629356 |
0,414196 |
|
0 |
0 |
0 |
0 |
0 |
1 |
0,893605 |
-0,09489 |
2,282568 |
|
0 |
0 |
0 |
0 |
0 |
0 |
-26,6098 |
38,91586 |
28,52867 |
|
0 |
0 |
0 |
0 |
0 |
0 |
-0,6831 |
-2,36391 |
8,457376 |
|
1 |
0,39166667 |
-0,14167 |
-0,15833 |
0 |
-0,50833 |
0,733333 |
-1,08333 |
-2,08333 |
|
0 |
1 |
-0,20996 |
-1,33983 |
-1,08225 |
-0,67316 |
-0,49134 |
0,800866 |
-0,64935 |
|
0 |
0 |
1 |
1,304515 |
0,698263 |
0,69701 |
2,877345 |
-2,11982 |
-0,54498 |
|
0 |
0 |
0 |
1 |
0,829345 |
0,439775 |
0,46505 |
-0,59187 |
0,615757 |
|
0 |
0 |
0 |
0 |
1 |
-0,00905 |
-0,79881 |
0,629356 |
0,414196 |
|
0 |
0 |
0 |
0 |
0 |
1 |
0,893605 |
-0,09489 |
2,282568 |
|
0 |
0 |
0 |
0 |
0 |
0 |
1 |
-1,46246 |
-1,07211 |
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
-3,36292 |
7,725015 |
|
1 |
0,39166667 |
-0,14167 |
-0,15833 |
0 |
-0,50833 |
0,733333 |
-1,08333 |
-2,08333 |
|
0 |
1 |
-0,20996 |
-1,33983 |
-1,08225 |
-0,67316 |
-0,49134 |
0,800866 |
-0,64935 |
|
0 |
0 |
1 |
1,304515 |
0,698263 |
0,69701 |
2,877345 |
-2,11982 |
-0,54498 |
|
0 |
0 |
0 |
1 |
0,829345 |
0,439775 |
0,46505 |
-0,59187 |
0,615757 |
|
0 |
0 |
0 |
0 |
1 |
-0,00905 |
-0,79881 |
0,629356 |
0,414196 |
|
0 |
0 |
0 |
0 |
0 |
1 |
0,893605 |
-0,09489 |
2,282568 |
|
0 |
0 |
0 |
0 |
0 |
0 |
1 |
-1,46246 |
-1,07211 |
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
-2,29711 |
Теперь при помощи "обратного хода" найдем неизвестные:
|
X1= |
38,9164615 |
|
X2= |
36,6211551 |
|
X3= |
12,3757444 |
|
X4= |
-7,24450326 |
|
X5= |
12,5899265 |
|
X6= |
9,38223372 |
|
X7= |
-13,769679 |
|
X8= |
-9,78120737 |
Решение системы линейных уравнений методом Крамера
|
12 |
4,7 |
-1,7 |
-1,9 |
0 |
-6,1 |
8,8 |
-13 |
-25 |
|
2,4 |
-8,3 |
1,6 |
12 |
10 |
5 |
6,3 |
-10 |
1 |
|
9,6 |
0 |
-7,1 |
-5 |
-0,49 |
-6,9 |
-9,9 |
0,43 |
-14 |
|
12 |
-7,3 |
-4,9 |
-11 |
-5,7 |
-9,8 |
-10 |
0 |
-25 |
|
-4,3 |
-3,7 |
14 |
-7,9 |
7,8 |
0 |
6,1 |
4,8 |
-5,9 |
|
-8,7 |
5,6 |
14 |
-5,5 |
0,41 |
-11 |
3,8 |
2,3 |
-30 |
|
6,1 |
3,9 |
7,4 |
3,2 |
-13 |
-11 |
0,4 |
11 |
-23 |
|
1,8 |
-11 |
-0,95 |
-7,9 |
-10 |
12 |
6 |
0 | 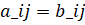
36 |
Det A= 305594473
Заменим первый столбец матрицы, и высчитаем определитель (Det A1)
|
-25 |
4,7 |
-1,7 |
-1,9 |
0 |
-6,1 |
8,8 |
-13 |
-25 |
|
1 |
-8,3 |
1,6 |
12 |
10 |
5 |
6,3 |
-10 |
1 |
|
-14 |
0 |
-7,1 |
-5 |
-0,49 |
-6,9 |
-9,9 |
0,43 |
-14 |
|
-25 |
-7,3 |
-4,9 |
-11 |
-5,7 |
-9,8 |
-10 |
0 |
-25 |
|
-5,9 |
-3,7 |
14 |
-7,9 |
7,8 |
0 |
6,1 |
4,8 |
-5,9 |
|
-30 |
5,6 |
14 |
-5,5 |
0,41 |
-11 |
3,8 |
2,3 |
-30 |
|
-23 |
3,9 |
7,4 |
3,2 |
-13 |
-11 |
0,4 |
11 |
-23 |
|
36 |
-11 |
-0,95 |
-7,9 |
-10 |
12 |
6 |
0 |
36 |
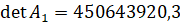
Отсюда вычислим
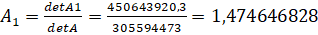
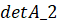
Далее по аналогии заменим второй столбец матрицы, и высчитаем определитель () итд.
|
12 |
-25 |
-1,7 |
-1,9 |
0 |
-6,1 |
8,8 |
-13 |
-25 |
|
2,4 |
1 |
1,6 |
12 |
10 |
5 |
6,3 |
-10 |
1 |
|
9,6 |
-14 |
-7,1 |
-5 |
-0,49 |
-6,9 |
-9,9 |
0,43 |
-14 |
|
12 |
-25 |
-4,9 |
-11 |
-5,7 |
-9,8 |
-10 |
0 |
-25 |
|
-4,3 |
-5,9 |
14 |
-7,9 |
7,8 |
0 |
6,1 |
4,8 |
-5,9 |
|
-8,7 |
-30 |
14 |
-5,5 |
0,41 |
-11 |
3,8 |
2,3 |
-30 |
|
6,1 |
-23 |
7,4 |
3,2 |
-13 |
-11 |
0,4 |
11 |
-23 |
|
1,8 |
36 |
-0,95 |
-7,9 |
-10 |
12 |
6 |
0 |
36 |
|
Определитель | ||
|
679335234,6 |
X2= |
2,222995815 |
|
12 |
4,7 |
-25 |
-1,9 |
0 |
-6,1 |
8,8 |
-13 |
-25 |
|
2,4 |
-8,3 |
1 |
12 |
10 |
5 |
6,3 |
-10 |
1 |
|
9,6 |
0 |
-14 |
-5 |
-0,49 |
-6,9 |
-9,9 |
0,43 |
-14 |
|
12 |
-7,3 |
-25 |
-11 |
-5,7 |
-9,8 |
-10 |
0 |
-25 |
|
-4,3 |
-3,7 |
-5,9 |
-7,9 |
7,8 |
0 |
6,1 |
4,8 |
-5,9 |
|
-8,7 |
5,6 |
-30 |
-5,5 |
0,41 |
-11 |
3,8 |
2,3 |
-30 |
|
6,1 |
3,9 |
-23 |
3,2 |
-13 |
-11 |
0,4 |
11 |
-23 |
|
1,8 |
-11 |
36 |
-7,9 |
-10 |
12 |
6 |
0 |
36 |
|
Определитель | ||
|
1299386781 |
X3= |
4,251996996 |
|
12 |
4,7 |
-1,7 |
-25 |
0 |
-6,1 |
8,8 |
-13 |
-25 |
|
2,4 |
-8,3 |
1,6 |
1 |
10 |
5 |
6,3 |
-10 |
1 |
|
9,6 |
0 |
-7,1 |
-14 |
-0,49 |
-6,9 |
-9,9 |
0,43 |
-14 |
|
12 |
-7,3 |
-4,9 |
-25 |
-5,7 |
-9,8 |
-10 |
0 |
-25 |
|
-4,3 |
-3,7 |
14 |
-5,9 |
7,8 |
0 |
6,1 |
4,8 |
-5,9 |
|
-8,7 |
5,6 |
14 |
-30 |
0,41 |
-11 |
3,8 |
2,3 |
-30 |
|
6,1 |
3,9 |
7,4 |
-23 |
-13 |
-11 |
0,4 |
11 |
-23 |
|
1,8 |
-11 |
-0,95 |
36 |
-10 |
12 |
6 |
0 |
36 |
|
Определитель | ||
|
4796433,406 |
X4= |
0,015695419 |
|
12 |
4,7 |
-1,7 |
-1,9 |
-25 |
-6,1 |
8,8 |
-13 |
-25 |
|
2,4 |
-8,3 |
1,6 |
12 |
1 |
5 |
6,3 |
-10 |
1 |
|
9,6 |
0 |
-7,1 |
-5 |
-14 |
-6,9 |
-9,9 |
0,43 |
-14 |
|
12 |
-7,3 |
-4,9 |
-11 |
-25 |
-9,8 |
-10 |
0 |
-25 |
|
-4,3 |
-3,7 |
14 |
-7,9 |
-5,9 |
0 |
6,1 |
4,8 |
-5,9 |
|
-8,7 |
5,6 |
14 |
-5,5 |
-30 |
-11 |
3,8 |
2,3 |
-30 |
|
6,1 |
3,9 |
7,4 |
3,2 |
-23 |
-11 |
0,4 |
11 |
-23 |
|
1,8 |
-11 |
-0,95 |
-7,9 |
36 |
12 |
6 |
0 |
36 |
|
Определитель | ||
|
-496757380,1 |
X5= |
-1,625544386 |
|
12 |
4,7 |
-1,7 |
-1,9 |
0 |
-25 |
8,8 |
-13 |
-25 |
|
2,4 |
-8,3 |
1,6 |
12 |
10 |
1 |
6,3 |
-10 |
1 |
|
9,6 |
0 |
-7,1 |
-5 |
-0,49 |
-14 |
-9,9 |
0,43 |
-14 |
|
12 |
-7,3 |
-4,9 |
-11 |
-5,7 |
-25 |
-10 |
0 |
-25 |
|
-4,3 |
-3,7 |
14 |
-7,9 |
7,8 |
-5,9 |
6,1 |
4,8 |
-5,9 |
|
-8,7 |
5,6 |
14 |
-5,5 |
0,41 |
-30 |
3,8 |
2,3 |
-30 |
|
6,1 |
3,9 |
7,4 |
3,2 |
-13 |
-23 |
0,4 |
11 |
-23 |
|
1,8 |
-11 |
-0,95 |
-7,9 |
-10 |
36 |
6 |
0 |
36 |
|
Определитель | ||
|
1841101860 |
X6= |
6,024656931 |
|
12 |
4,7 |
-1,7 |
-1,9 |
0 |
-6,1 |
-25 |
-13 |
-25 |
|
2,4 |
-8,3 |
1,6 |
12 |
10 |
5 |
1 |
-10 |
1 |
|
9,6 |
0 |
-7,1 |
-5 |
-0,49 |
-6,9 |
-14 |
0,43 |
-14 |
|
12 |
-7,3 |
-4,9 |
-11 |
-5,7 |
-9,8 |
-25 |
0 |
-25 |
|
-4,3 |
-3,7 |
14 |
-7,9 |
7,8 |
0 |
-5,9 |
4,8 |
-5,9 |
|
-8,7 |
5,6 |
14 |
-5,5 |
0,41 |
-11 |
-30 |
2,3 |
-30 |
|
6,1 |
3,9 |
7,4 |
3,2 |
-13 |
-11 |
-23 |
11 |
-23 |
|
1,8 |
-11 |
-0,95 |
-7,9 |
-10 |
12 |
36 |
0 |
36 |
|
Определитель | ||
|
-1354259550 |
X7= |
-4,431557733 |
|
12 |
4,7 |
-1,7 |
-1,9 |
0 |
-6,1 |
8,8 |
-25 |
|
2,4 |
-8,3 |
1,6 |
12 |
10 |
5 |
6,3 |
1 |
|
9,6 |
0 |
-7,1 |
-5 |
-0,49 |
-6,9 |
-9,9 |
-14 |
|
12 |
-7,3 |
-4,9 |
-11 |
-5,7 |
-9,8 |
-10 |
-25 |
|
-4,3 |
-3,7 |
14 |
-7,9 |
7,8 |
0 |
6,1 |
-5,9 |
|
-8,7 |
5,6 |
14 |
-5,5 |
0,41 |
-11 |
3,8 |
-30 |
|
6,1 |
3,9 |
7,4 |
3,2 |
-13 |
-11 |
0,4 |
-23 |
|
1,8 |
-11 |
-0,95 |
-7,9 |
-10 |
12 |
6 |
36 |
|
Определитель | ||
|
-701985512,8 |
X8= |
-2,297114558 |
|
X1= |
1,47464683 |
|
X2= |
2,22299582 |
|
X3= |
4,251997 |
|
X4= |
0,01569542 |
|
X5= |
-1,62554439 |
|
X6= |
6,02465693 |
|
X7= |
-4,43155773 |
|
X8= |
-2,29711456 |
Заключение
Мы выяснили, что выбор метода решения не влияет на конечный результат, так как ответы, полученные вследствие решения различными методами совпадают.
Список литературы
- 1. В. А. Ильин, Э. Г. Поздняк; Линейная Алгебра; 4 изд.; Москва ФизМатЛит 2002г.; стр. 12, §1.1 2. Л. И. Лопатников; Экономико-математический словарь: Словарь современной экономической науки; 5-е изд., перераб. и доп.; Москва: Дело, 2003. (эл. версия: http://slovari. yandex. ru/определитель%20матрицы/Лопатников/Определитель%20матрицы/) 3. http://ru. wikipedia. org/wiki/Метод_Гаусса 4. http://ru. math. wikia. com/wiki/Метод_Крамера
Похожие статьи
-
Системы линейных уравнений - Методы решения системы линейных уравнений
Системой m линейных уравнений с n неизвестными называется система вида Где aIj и bI (i=1,...,m; b=1,...,n) - некоторые известные числа, а x1,...,xN -...
-
По теме "Вариант №2" Определить совместность системы линейных уравнений: Решение: А = RgA = 2. A* = RgA* = 3. Ответ. Система не совместима. 2. Вычислить...
-
Элементарные преобразования, Миноры - Методы решения системы линейных уравнений
Определение. Элементарными преобразованиями матрицы назовем следующие преобразования: 1) умножение строки на число, отличное от нуля; 2) прибавление к...
-
Определители (детерминанты) - Методы решения системы линейных уравнений
Определение. Определителем квадратной матрицы А= называется число, которое может быть вычислено по элементам матрицы по формуле: Det A = , где (1) М1к -...
-
МАТРИЦЫ И ОПЕРАЦИИ НАД НИМИ Матрицей A называется любая прямоугольная таблица, составленная из чисел, которые называют элементами матрицы и обозначается...
-
Линейные уравнения и системы линейных уравнений над кольцом целостности - Евклидовость в математике
Математическое предположение, которое может быть только истинным, или ложным, "существует столбец значений неизвестных такой, что соответствующие этому...
-
Алгоритмы метода Монте-Карло для решения интегральных уравнений второго рода Пусть необходимо вычислить линейный функционал , Где, причем для...
-
Решим прямую задачу линейного программирования симплексным методом, с использованием симплексной таблицы. Определим максимальное значение целевой...
-
Заключение - Системы эконометрических уравнений, их применение в эконометрике
В данной курсовой работе я рассмотрела методы восстановления временных зависимостей на основе наименьших квадратов и наименьших модулей. Среди них важное...
-
Особенности эконометрического метода Эконометрическая модель -- основное понятие эконометрии, экономико-математическая модель, параметры которой...
-
Ранг матрицы. - Методы решения системы линейных уравнений
Как было сказано Выше , минором матрицы порядка s называется определитель матрицы, образованной из элементов исходной матрицы, находящихся на пересечении...
-
Введение - Системы эконометрических уравнений, их применение в эконометрике
Объектом статистического изучения в социальных науках являются сложные системы. Измерение тесноты связей между переменными, построение изолированных...
-
Методы наименьших квадратов - Системы эконометрических уравнений, их применение в эконометрике
Как уже отмечалось, разработана масса методов эвристического анализа систем эконометрических уравнений. Они предназначены для решения тех или иных...
-
Элементы матричного анализа - Методы решения системы линейных уравнений
Вектором, как на плоскости, так и в пространстве, называется направленный Отрезок , то есть такой Отрезок , один из концов которого выделен и называется...
-
Уравнение линии на плоскости - Методы решения системы линейных уравнений
Как известно, любая точка на плоскости определяется двумя координатами в какой - либо системе координат. Системы координат могут быть различными в...
-
Известно оптимальное решение X*=(0;0;1;1) задачи линейного программирования: Составьте двойственную задачу и найдите ее оптимальное решение по теореме...
-
Любое частное решения уравнения (1) на координатной плоскости х0у изображено в виде графика функции у=у (х, с) (с=const). В теории дифференциальных...
-
Определение . Алгебраическим дополнением минора матрицы называется его Дополнительный минор , умноженный на (-1) в степени, равной сумме номеров строк и...
-
Применение систем эконометрических уравнений представляет собой непростую задачу. Проблемы здесь происходят из-за ошибок спецификации. Основной областью...
-
Например, если изучается модель спроса как соотношение цен и количества потребляемых товаров, то одновременно для прогнозирования спроса необходима...
-
Матрицы и определители - Методы решения системы линейных уравнений
Определение. Матрицей размера mn, где m - число строк, n - число столбцов, называется таблица чисел, расположенных в определенном порядке. Эти числа...
-
Как известно решение задач симплексным методом применяется очень часто. Это связано с тем, что симплексный метод подходит для решения широкого круга...
-
Исходная задача: При ограничениях: Двойственной является следующая задача: При ограничениях: Число неизвестных в двойственной задаче равно 2....
-
Тест - Решение уравнений и построение графиков функций, содержащих выражения со знаком модуля
Модуль уравнение неравенство график В приведенном ниже тесте четыре задания на решение уравнений и неравенств, содержащих знак модуля. Используются...
-
Метод дихотомии требует менее всего итераций цикла для получения корней уравнения с заданной точностью. Если расчет ведется без помощи ЭВМ, то это...
-
Провести комплексное исследование численных методов для задачи решения нелинейных уравнений. 1. Решить нелинейные уравнения А) ; Б) ; В) . 2....
-
Вид сырья Запас сырья Количество единиц сырья, идущих на изготовление единицы продукции P1 P2 P3 P4 S1 4 1 1 1 3 S2 18 2 4 6 1 Прибыль от единицы...
-
Введение - Решение оптимизационных экономических задач методами линейного программирования
Линейное программирование является составной частью раздела математики, который изучает методы нахождения условного экстремума функции многих переменных...
-
Математическая модель задачи нелинейного программирования (ЗНП) (*) Для ЗНП в отличие от Задачи Линейного Программирования (ЗЛП) нет единого метода...
-
Приведем систему ограничений к каноническому виду, для этого необходимо неравенства преобразовать в равенства, с добавлением дополнительных переменных....
-
Уравнение графический спрос равновесие С позиций воспитательного аспекта целью данного проекта является помощь учащимся в понимании жизненной...
-
В состав системы эконометрических уравнений входят множество зависимых или эндогенных переменных и множество предопределенных переменных (лаговые и...
-
Заключение - Метод представления знаний в интеллектуальных системах поддержки экспертных решений
Метод обобщенных интервальных оценок, предложенный в настоящей статье, является новым методом представления экспертных знаний в задачах, исходные данные...
-
Реализация интеллектуальных систем поддержки решений (ИСППР) в задачах оценки перспективности объектов природопользования на ранних стадиях их...
-
При неизменности всех прочих факторов снижение цены ведет к соответствующему увеличению спроса и, наоборот, при прочих равных условиях увеличение цены...
-
Свойства операции умножения матриц - Методы решения системы линейных уравнений
1)Умножение матриц не коммутативно, т. е. АВ ВА даже если определены оба произведения. Однако, если для каких - либо матриц соотношение АВ=ВА...
-
Наша группа работала над учебным межпредметным проектом "Математические модели в рыночной экономике". Мы покажем применение в экономике систем уравнений....
-
Литература - Метод представления знаний в интеллектуальных системах поддержки экспертных решений
Финн В. К. Интеллектуальные информационные системы. //Итоги науки и техники. Сер. Информатика. Т. 15. М.: ВИНИТИ. 1991. Финн В. К. Об особенностях...
-
Второй раздел курсовой работы посвящен особенностям постановки и решения общей задачи линейного программирования, а именно, транспортной задаче (ТЗЛП)....
-
Ответ: Функция y=arctgx, ее график, свойства Ответ: Функция y=arcctgx, ее график, свойства Ответ: Решение уравнений sinx=a, частные случаи Ответ:...
Решение систем линейных уравнений