Обгрунтування методу розв'язку задачі визначення оптимального горизонту планування амортизаційної стратегії - Взаємозв'язок між горизонтом планування й витратами на амортизацію для малого підприємства
В основі моделі (2.2.) - (2.6) лежить рівняння, яке має вигляд:
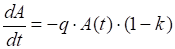
,
Зробимо просте перетворення, зробивши заміну:
(2.7)
І отримаємо рівняння (2.8):
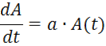
(2.8)
Розв'язавши це рівняння, з отриманої залежності вартості основних виробничих фондів від часу, можна знайти залежності чистого прибутку та обсягу фонду нагромадження в часі. З даних, при проведенні додаткових розрахунків будемо обгрунтовувати доцільність вибору тієї чі інщої амортизаційної стратегії, шукати оптимальний горизонт планування, при досягненні якого настане необхідність змінювати стратегію. Це рівняння є звичайним диференціальним рівнянням І-го порядку. Приведемо основні визначення та методи розв'язку звичайних диференціальних рівнянь.
Дослідження поведінки різних систем (технічні, економічні, екологічні та ін.) часто призводить до аналізу і розв'язку рівнянь, що включають як параметри системи, так і швидкості їх зміни, аналітичним вираженням яких є похідні. Такі рівняння, містять похідні, називаються диференціальними.
Дамо основні визначення стосовно теорії диференціальних рівнянь.
Диференціальним рівнянням називається рівняння, що містить незалежну змінну, невідому функцію та її похідні, тобто рівняння виду:
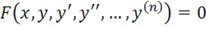
.
Порядком диференціального рівняння називається найвищий порядок похідної, що входить до нього.
Рішенням диференціального рівняння називається всяка функція, яка при підстановці в рівняння обертає його в тотожність.
Процедура пошуку розв'язку диференціального рівняння називається його інтегруванням, а графіки його рішень - інтегральними кривими.
Всяке диференціальне рівняння порядку має незліченну множину розв'язків. Всі ці розв'язки визначаються функцією, яка містить довільних постійних. Ця сукупність розв'язків називається загальним розв'язком диференціального рівняння. Частковим рішенням диференціального рівняння називається всяка функція цієї сукупності, що відповідає конкретному набору постійних.
Геометрично загальний розв'язок диференціального рівняння являє собою сімейство інтегральних кривих площині, а часткове рішення - конкретну криву цього сімейства.
Початковими умовами для диференціального рівняння порядку n називається набір значень функції та її похідних порядку n-1 включно в деякій точці.
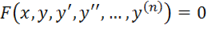
Задачею Коші називається задача про відшукання розв'язку диференціального рівняння, що задовольняє заданим початковим умовам:
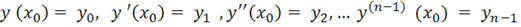
.
Геометрично це означає, що в загальному рішенні рівняння необхідно так підібрати константи, щоб відповідна їм інтегральна крива проходила через точку площини і в цій точці мала задані значення всіх своїх похідних до порядку.
Теорема про існування та єдності розв'язку задачі Коші:
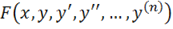
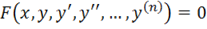
Якщо функція безперервно диференційована в деякій області, яка містить точку, то в цій області існує і притому єдиний розвязок диференціального рівняння, яке задовольняє заданим початковим умовам:
Загальних методів розв'язку диференціальних рівнянь першого порядку не існує, однак для деяких важливих класів функцій такі методи відомі і призводять до загального розв'язку рівняння.
Оскільки в моделі зазначено звичайне диференціальне рівняння І-го порядку, то дамо визначення такого рівняння та опишемо основні методи розв'язку таких рівнянь.
Диференціальне рівняння першого порядку є рівнянням виду
Далі ми будемо вважати, що це рівняння записано відносно похідної: . Це рівняння так само можна записати в диференціальної формі:
.
Загальних методів розв'язку диференціальних рівнянь першого порядку не існує, однак для деяких важливих класів функцій такі методи відомі і призводять до загального розв'язку рівняння. Розглянемо деякі з цих класів.
Рівняннями з відокремлюваними змінними називаються рівняння, права частина яких представляє собою добуток функції, що залежить тільки від, і функції, що залежить тільки від.
Горизонт планування амортизаційний витрата
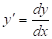
Для пошуку рішення такого рівняння виразимо похідну, що входить у нього через диференціали і перейдемо до рівняння в диференціалах:
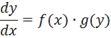
Тепер розділимо змінні:
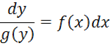
(В останньому рівнянні змінні і поділяє знак рівності).
Проінтегрувавши обидві частини останньої рівності отримає загальний розв'язок рівняння у вигляді неявно заданої функції:
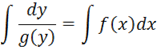
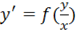
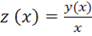
Однорідні рівняння. Так називаються рівняння виду. За допомогою заміни змінної це рівняння може бути зведене до рівняння з відокремлюваними змінними.
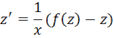
Розв'язавши це рівняння, знайдемо функцію, а з нею і розв'язок вихідного рівняння
Лінійними рівняннями називаються диференціальні рівняння виду
Рішення цього рівняння будемо шукати у вигляді добутку двох функцій ). Тоді і щодо функцій і рівняння прийме вигляд:
Замість однієї невідомої функції ми ввели в розгляд дві функції і тому однією з них ми можемо розпорядитися на свій розсуд. Виберемо функцію так, щоб доданок в дужках у лівій частині останнього рівняння звертався в нуль. Для цього в якості достатньо взяти будь-який розв'язок рівняння із відокремлюваними змінними:
Розділяючи змінні і інтегруючи, отримаємо
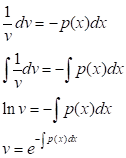
Таким чином, в якості достатньо взяти функцію
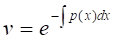
При цьому ми можемо вважати, що константа, що виникає в результаті обчислення інтеграла, дорівнює нулю. При такому виборі функції для функції отримуємо рівняння:
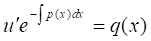
,
Або
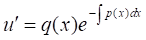
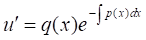
Інтегруючи останнє рівняння, одержимо
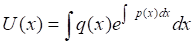
Коли функції і знайдені, загальний розв'язок лінійного рівняння знаходиться без зусиль.
Методи Рунге - Кутта - важливе сімейство чисельних алгоритмів розв'язання звичайних диференціальних рівнянь та їх систем. Дані ітеративні методи явного і неявного наближеного обчислення були розроблені у 1900 році німецькими математиками К. Рунге і М. В. Куттою.
Формально, методом Рунге - Кутта є модифікований і виправлений метод Ейлера, він представляє собою схему другого порядку точності. Існують стандартні схеми третього порядку, які не отримали широкого розповсюдження. Найбільш часто використовується і реалізована в різних математичних пакетах стандартна схема четвертого порядку. Побудова схем більш високого порядку пов'язане з великими обчислювальними труднощами.
Розглянемо задачу Коші для диференціального рівняння довільного порядку, що записується у векторній формі як:
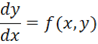
Тоді значення невідомої функції в точці обчислюється відносно значення в попередній точці за формулою:
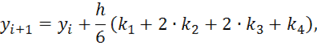
Де - крок інтегрування, а коефіцієнти розраховуються таким чином:
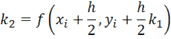
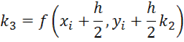
Це метод 4-го порядку, тобто похибка на кожному кроці становить, а сумарна похибка на кінцевому інтервалі інтегрування є величиною
Оскільки диференціальне рівняння, що представлене в моделі є диференціальним рівнянням першого порядку з відокремлюваними змінними, то це рівняння доцільніше буде розв'язати аналітично, оскільки цей метод є точним і не потребує великої кількості обчислень.
Похожие статьи
-
Основні принципи застосування економіко-математичного аналізу до діяльності малих підприємств закладені в роботах [1,2,3]. Запропоновані методи...
-
Постановка завдання необхідності використання амортизаційних відрахувань для малого підприємства Найважливішими проблемами сучасності є подолання...
-
Постановка і актуальність завдання дослідження Мале підприємство, що функціонує в умовах становлення ринкових відносин, є самостійним економічним агентом...
-
Досить універсальним методом розв'язку лінійних однорідних систем з сталими коефіцієнтами є матричний метод. Він полягає в наступному. Розглядається...
-
ВСТУП - Взаємозв'язок між горизонтом планування й витратами на амортизацію для малого підприємства
Коли мале підприємство починає новий проект, то одне з питань, що має бути вирішеним, - це стратегія амортизаційної політики. Оскільки виділення коштів...
-
Диференціал, Визначення диференціала. - Основи вищої математики
Визначення диференціала. Формули й правила диференціювання. Використання диференціала для наближених обчислень. Основні теореми диференціального...
-
Метод дифференциальных рент для решения транспортной задачи - Формирование оптимального штата фирмы
Для решения транспортных задач используется несколько методов. Рассмотрим решение с помощью метода дифференциальных рент. При нахождении решения...
-
В разделе 1 курсовой работы требуется: Определить количество закупаемого заданным филиалом фирмы сырья у каждого АО, (xj), максимизируя прибыль филиала....
-
Условие задачи. Пусть имеются n кандидатов для выполнения этих работ. Назначение кандидата i на работу j связано с затратами CIj (i, j = 1,2,..., n)....
-
Розробка математичного забезпечення інформаційної системи Характеристика моделей і методів рішення економічної задачі Фінансовий аналіз здійснюється за...
-
Метод дихотомии требует менее всего итераций цикла для получения корней уравнения с заданной точностью. Если расчет ведется без помощи ЭВМ, то это...
-
Решение смешанной задачи для уравнения теплопроводности методом конечных разностей
Решение смешанной задачи для уравнения теплопроводности методом конечных разностей 1. Цель работы Ознакомление с методами решения смешанных задач для...
-
Для побудови алгоритмів розв'язання задач матричних ігор використовується властивість оптимальних змішаних стратегій: оптимальна змішана стратегія...
-
Задача о загрузке рюкзака (задача о ранце) - Метод динамического программирования для решения задач
Постановка задачи. Пусть имеются N видов грузов с номерами. Единица груза j-го вида имеет все aJ. Если груз j-го вида берется в количестве xJ, то его...
-
Как известно решение задач симплексным методом применяется очень часто. Это связано с тем, что симплексный метод подходит для решения широкого круга...
-
Задание для исследования - Численное нахождение корня уравнения методом Рунге-Кутта
Исследовать решение обыкновенных дифференциальных уравнений методом Рунге-Кутты. Подробное описание Метод этот пригоден для решения как одиночных...
-
Система диференціальних рівнянь вигляду Де - сталі величини, називається лінійною однорідною системою з сталими коефіцієнтами. У матричному вигляді вона...
-
Динамическое программирование Динамическое программирование -- один из разделов оптимального программирования, в котором процесс принятия решения и...
-
ЗАТ "Біола" випускає три види продукції: напій на основі сиропу з цукром, напій на основі сиропу з цукрозамінником, сік. У поточному місяці прогнозуються...
-
Розв'язання систем рівнянь, Порядок виконання роботи - Вивчення математичного пакету MathСad
Матриця математичний пакет арифметичний Для розв'язання системи рівнянь з кількома невідомими треба задати початкові наближення для кожної змінної. Далі...
-
У роботі розглядаються безперервні функції F З періодом 2p і їх наближення тригонометричними поліномами. Через Tn(x) Позначається тригонометричний...
-
Кореляційний і регресивний методи аналізу зв'язку
Кореляційний і регресивний Методи аналізу зв'язку Основне завдання кореляційного і регресійного методів полягає в аналізі статистичних даних для...
-
Теоретичні основи оптимізаційних рішень Умови оптимальності у формі принципу максимуму дають, узагалі говорячи, достатню інформацію для рішення задачі...
-
Біологія . Необхідно знайти залежність площі молодого листка, що має форму круга, від часу. Відомо, що швидкість зміни площі в момент пропорцією площі...
-
Второй раздел курсовой работы посвящен особенностям постановки и решения общей задачи линейного программирования, а именно, транспортной задаче (ТЗЛП)....
-
Модуль ARIS ABS реалізує аналіз вартості процесів, при якому структура витрат повністю прозора, на відміну від методу встановлених нормативами...
-
Вероятностные характеристики полумарковской модели Формулы для условных вероятностей Обозначим Теорема 1. В рассматриваемой стохастической полумарковской...
-
Провести комплексное исследование численных методов для задачи решения нелинейных уравнений. 1. Решить нелинейные уравнения А) ; Б) ; В) . 2....
-
Пусть имеется оптимизационная задача вида: (1) (2) (3) - задан(4) Здесь предполагается, что FJ(xJ,yJ)>0 для всех допустимых значений xJ,yJ. В этом случае...
-
Аналізуючи результати, які були отримані у другому розділі роботи щодо фінансово-господарського стану підприємства, можна зробити висновки про...
-
Найти при помощи метода ячеек значение интеграла , Где - область, ограниченная функциями . 2. Теоретическая часть Рассмотрим K-мерный интеграл вида: (1)...
-
Адсорбционные методы исследования свойств поверхности позволяют количественно охарактеризовать происходящие при адсорбции межмолекулярные взаимодействия,...
-
Регрессия -- зависимость среднего значения какой-либо величины от некоторой другой величины или от нескольких величин. Задача регрессионного анализа...
-
Задача регрессии. Метод наименьших квадратов Ищу функцию регрессии в виде (1*). Оценки коэффициентов нахожу с помощью Метода Наименьших Квадратов (МКВ),...
-
Под действием видимого, ультрафиолетового и более коротковолнового излучения фуллерены полимеризуются и в таком виде не растворяются органическими...
-
Транспортная задача - Экономико-математические методы
Методы линейного программирования, являются хорошим инструментом для решения ряда проблем распределения ресурсов. Применение пакетов прикладных программ...
-
Цель и задачи исследования операций Исследование операций - научная дисциплина, занимающаяся разработкой и практическим применением методов наиболее...
-
Исходная задача: При ограничениях: Двойственной является следующая задача: При ограничениях: Число неизвестных в двойственной задаче равно 2....
-
В этом случае лучшим считается вариант, у которого суммарная величина отдельных целевых функций принимает максимальное значение: F Max = = max...
-
Основные понятия теории экономико-математического моделирования Кибернетический подход к исследованию экономико-математических систем Обычно...
Обгрунтування методу розв'язку задачі визначення оптимального горизонту планування амортизаційної стратегії - Взаємозв'язок між горизонтом планування й витратами на амортизацію для малого підприємства