Алгоритм приведення матричної гри до задачі лінійного програмування - Оптимальне планування виробництва методами лінійного програмування
Для побудови алгоритмів розв'язання задач матричних ігор використовується властивість оптимальних змішаних стратегій: оптимальна змішана стратегія першого гравця гарантує йому виграш не менший ціни гри за будь-яких стратегій другого гравця і рівній ціні гри за оптимальної стратегії другого гравця. Використання названої властивості матричних ігор дає можливість привести задачу пошуку оптимальних змішаних стратегій до задачі лінійного програмування. Розглянемо одну з методик побудови відповідного алгоритму[9].
Маємо матричну гру за відомої матриці
H = {hIj} (I=1,2,..., m; j=1,2,..., n).
Перший гравець має чисті стратегії А1, А2,..., Аm, другий - В1, В2,...,Вn. Необхідно знайти оптимальні змішані стратегії
SA0 =(p10,p20,..., pM0) та SB0 =(g10, g20,..., gM0),
Де pI0 та gJ0 - ймовірності використання відповідних чистих стратегій гравцями.
Використовуючи можливість афінних перетворень матриці, без застережень можна вважати, що hIj>=0 і V >0.
Якщо перший гравець використовує свою оптимальну змішану стратегію
SA0=(p10, p20,...,pM0)
Проти будь-якої чистої стратегії BIj другого гравця, то його очікуваний гарантований виграш, тобто математичне сподівання виграшу
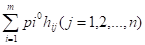
HJ =.
Наголосимо, що значення {pI0} поки що невідомі. За оптимальної стратегії
SA0= (p10, p20,..., pM0)
Гравця А його середні виграші за будь-якої чистої стратегії супротивника будуть не менше ціни гри V, тому можемо записати і гарантувати виконання системи:
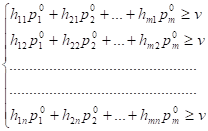
(2.2)
Кожну з наведених нерівностей помножимо на 1/V і введемо нові зміни:
X1=p10/v; x2=p20/v;......;xM=pM0/v.
За нових змінних система запишеться так:
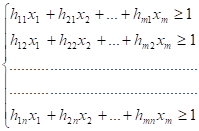
(2.3)
Скориставшись умовою
P10+p20+...+pM0 =1
(сума всіх ймовірних дорівнює ймовірності достовірної події) та, маємо:
X1+x2+...+xM =1/v.
Мета першого гравця - максимізувати гарантований виграш, тобто ціну гри V. Але максимізація ціни гри V обумовлює мінімізацію величини 1/V, тому розв'язання задачі пошуку величин x1,x2..., xM Можна сформулювати так: знайти величини змінних xI так, щоб вони задовольняли системі лінійних обмежень за умови досягнення найменшого значення лінійної функції:
Z=x1+ x2+...+ xM.
Розв'язавши сформульовану задачу лінійного програмування та скориставшись, одержуємо оптимальну змішану стратегію для першого гравця
Та максимальний гарантований виграш V.
Для розв'язання задачі пошуку оптимальних змішаних стратегій
Другого гравця використовуються умови:
- 1. середній очікуваний програш другого гравця за умови використання ним оптимальної стратегії не перевищує ціни гри, які б стратегії не використовував перший гравець; 2. гравець В прагне мінімізувати свій гарантований програш, тобто досягти максимуму величини 1/V.
За названих умов змінні g10, g20,..., gN0 задовольняють нерівностям:
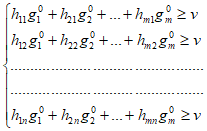
(2.4)
Якщо ввести нові змінні
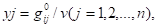
То система матиме вигляд:
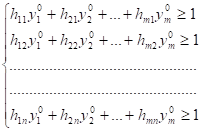
(2.5)
До того ж змінні мають задовольнити умові:
Таким чином, розв'язання задачі пошуку оптимальних стратегій для другого гравця приведено до задачі лінійного програмування: знайти величини змінних так, щоб вони задовольняли системі лінійних обмежень за умови досягнення найбільшого значення лінійної функції:
Порівнявши задачі лінійного програмування, до яких зведені задачі пошуку оптимальних стратегій задачі матричної гри, робимо висновок, що названі задачі лінійного програмування спряжені. Доцільно наголосити, що для пошуку оптимальних змішаних стратегій у конкретній моделі задачі гри треба вибирати ту із взаємно спряжених задач, розв'язок якої легше знайти, а розв'язок другої знаходити, використовуючи теореми спряженості.
Похожие статьи
-
ЗАТ "Біола" випускає три види продукції: напій на основі сиропу з цукром, напій на основі сиропу з цукрозамінником, сік. У поточному місяці прогнозуються...
-
Вступ - Оптимальне планування виробництва методами лінійного програмування
Поступовий перехід України від централізовано-планової системи господарювання до ринкової по-новому ставить питання про методи ведення економіки...
-
Динамическое программирование Динамическое программирование -- один из разделов оптимального программирования, в котором процесс принятия решения и...
-
Исходная задача: При ограничениях: Двойственной является следующая задача: При ограничениях: Число неизвестных в двойственной задаче равно 2....
-
Транспортная задача - Экономико-математические методы
Методы линейного программирования, являются хорошим инструментом для решения ряда проблем распределения ресурсов. Применение пакетов прикладных программ...
-
Для достижения поставленной цели предприятию требуются материалы, оборудование, энергия, рабочая сила и другие ресурсы. Каждое предприятие такими...
-
Линейное программирование, Общая задача линейного программирования - Экономико-математические методы
Термин "линейное программирование" впервые появился в 1951 г. в работах американских ученых (Дж. Данциг, Т. Купманс), а первые исследования по линейному...
-
Цель и задачи исследования операций Исследование операций - научная дисциплина, занимающаяся разработкой и практическим применением методов наиболее...
-
Условие задачи. Пусть имеются n кандидатов для выполнения этих работ. Назначение кандидата i на работу j связано с затратами CIj (i, j = 1,2,..., n)....
-
Теория: Применяется, как правило, для задач линейного программирования, содержащих не более 2 переменных. Суть геометрического метода сводится к...
-
В разделе 1 курсовой работы требуется: Определить количество закупаемого заданным филиалом фирмы сырья у каждого АО, (xj), максимизируя прибыль филиала....
-
Решение смешанной задачи для уравнения теплопроводности методом конечных разностей
Решение смешанной задачи для уравнения теплопроводности методом конечных разностей 1. Цель работы Ознакомление с методами решения смешанных задач для...
-
Регрессия -- зависимость среднего значения какой-либо величины от некоторой другой величины или от нескольких величин. Задача регрессионного анализа...
-
Решим прямую задачу линейного программирования симплексным методом, с использованием симплексной таблицы. Определим максимальное значение целевой...
-
Календарный производственный программирование однооперационный Все существующие методы решения задач календарного планирования3 по степени достижения...
-
Пусть имеется оптимизационная задача вида: (1) (2) (3) - задан(4) Здесь предполагается, что FJ(xJ,yJ)>0 для всех допустимых значений xJ,yJ. В этом случае...
-
Основные понятия теории экономико-математического моделирования Кибернетический подход к исследованию экономико-математических систем Обычно...
-
Задача о загрузке рюкзака (задача о ранце) - Метод динамического программирования для решения задач
Постановка задачи. Пусть имеются N видов грузов с номерами. Единица груза j-го вида имеет все aJ. Если груз j-го вида берется в количестве xJ, то его...
-
Теоретическое обоснование математического моделирования - Математические методы и модели в экономике
Коммерческая деятельность в том или ином виде сводится к решению таких задач: как распорядиться имеющимися ресурсами для достижения наибольшей выгоды или...
-
Инвестиционный портфель оптимальный многокритериальный В качестве тестового примера использовались следующие входные данные [Социальная сеть инвесторов,...
-
Рассматриваемая задача оптимизации ИП основывается на двухкритериальной модели Г. Марковица с незначительной корректировкой (вместо поиска долей каждого...
-
Задачи статистики - Предмет, метод и задачи статистической науки
Главной задачей статистики является получение и соответствующая обработка статистической информации для принятия решений направленных на достижение...
-
Наличие особых ситуаций на террайне зависит от характеристик его сложности. Ниже приведена возможная классификационная схема характеристик сложности...
-
Второй раздел курсовой работы посвящен особенностям постановки и решения общей задачи линейного программирования, а именно, транспортной задаче (ТЗЛП)....
-
В инженерной практике в настоящее время широко используются современные программные комплексы позволяющие моделировать сложные физические процессы. Для...
-
В начале пятилетнего периода работы предприятию выделена сумма в C руб. для приобретения нового оборудования. Стоимость одного комплекта оборудования...
-
Задача регрессии. Метод наименьших квадратов Ищу функцию регрессии в виде (1*). Оценки коэффициентов нахожу с помощью Метода Наименьших Квадратов (МКВ),...
-
Экономические задачи, сводящиеся к транспортным моделям - Экономико-математические методы
Алгоритмы и методы решения транспортной задачи могут быть использованы при решении некоторых экономических задач, не имеющих ничего общего с...
-
ОБЩАЯ ПОСТАНОВКА ЗАДАЧИ ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ (ЗЛП) - Линейное программирование в экономике
Линейное программирование - направление математики, изучающее методы решения экстремальных задач, которые характеризуются линейной зависимостью между...
-
Известно оптимальное решение X*=(0;0;1;1) задачи линейного программирования: Составьте двойственную задачу и найдите ее оптимальное решение по теореме...
-
Транспортные задачи, имеющие некоторые усложнения в постановке - Экономико-математические методы
Транспортная задача с избытком запасов: Для отыскания оптимального плана вводят фиктивный (n+1)-й пункт назначения Bn+1 с потребностью bn+1 и полагают...
-
Пример решения транспортной задачи - Экономико-математические методы
На четырех строительных площадках В1, В2, В3, В4 монтируется в день соответственно 20,120,20 60 м3 сборных плит перекрытий. Производство этих плит...
-
Решение транспортной задачи методом потенциалов - Математическая модель решения транспортной задачи
Этот метод позволяет автоматически выделять циклы с отрицательной ценой и определять их цены. Пусть имеется транспортная задача с балансовыми условиями...
-
Общая постановка задачи исследования операций - Экономико-математические методы
Все факторы, входящие в описание операции, можно разделить на две группы: Постоянные факторы (условия проведения операции), на которые мы влиять не...
-
Модели и моделирование - Экономико-математические методы
Одним из основных методов научного познания является эксперимент, а самой распространенной его разновидностью - метод моделирования систем. В процессе...
-
Постановка задачі - Економетричні моделі
Задача. Для виготовлення чотирьох видів продукції використовують три види сировини. Запаси сировини, норми його витрати і прибуток від реалізації...
-
Введение - Экономико-математические методы
Экономические проблемы, возникающие перед специалистами, в большинстве своем сложные. Они зависят от множества различных, иногда противоречащих друг...
-
Как известно решение задач симплексным методом применяется очень часто. Это связано с тем, что симплексный метод подходит для решения широкого круга...
-
Математическая модель транспортной задачи: F = ??cIjXIj, (1) При условиях: ?xIj = aI, i = 1,2,..., m, (2) ?xIj = bJ, j = 1,2,..., n, (3)...
-
Расчет верхней и нижней границы надежности схемы методом минимальных путей и сечений Как видно из схемы, она не является последовательно-параллельной,...
Алгоритм приведення матричної гри до задачі лінійного програмування - Оптимальне планування виробництва методами лінійного програмування