Алгоритм Метрополиса - Метод Монте Карло в химическом моделировании
В случае сложных жидкостей практически невозможно точно рассчитать значение конфигурационной статистической суммы системы. Однако его можно оценить с помощью метода статистических испытаний, генерируя конечный набор молекулярных конфигураций и определяя вероятность их появления wj

Wi = (1.10)
Если в некоторый фиксированный объем помещать случайным образом молекулы, энергия взаимодействия между которыми задается набором потенциальных функций, то в зависимости от конфигурации системы больцмановский множитель exp (- Ui /кТ) может принимать различные значения[11-17]. Некоторые конфигурации дают значительный вклад в канонические средние, а некоторые - практически нулевой (например, когда две частицы сближены настолько, что между ними имеется сильное отталкивание).
При случайной генерации конфигураций подавляющее их большинство будет давать вклад близкий нулю. Поэтому необходимо пользоваться методом существенной выборки, в соответствии с которым конфигурации генерируют с заданной функцией распределения вероятностей рi
Среднее по ансамблю от любой физической величины M рассчитывают по формуле


<M>= iexp(-)/= (1/11)

Где i - номер конфигурации (среднее берется по всем рассмотренным конфигурациям системы)[16]. Поскольку усреднение (1.11.) проводят по конечному числу конфигураций m со смещенной выборкой, для исключения влияния смещения каждую конфигурацию необходимо брать с весом 1/рi :

<M>? exp(-)/ (3)

Метрополис с соавторами [15-16] предложил в качестве рi взять распределение Больцмана

Рi = exp()/ (1.13)

В результате среднее значение любой физической величины M можно записать в виде
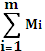
<M>? (1/m) (1.14)
Ансамбль, состоящий из m конфигураций, получают путем задания вероятностей перехода от одной конфигурации к другой. Вероятность перехода от i-й конфигурации к j-й pij считают зависящей от энергий этих конфигураций, а точнее от величины (Uj - Ui)/kT:
Рij = Pji exp[-(Uj - Ui)/kT] (1.15)
Таким образом, строят простые цепи Маркова, т. е. последовательности случайных событий, в которых вероятность определенного события зависит от исхода предыдущего испытания. В соответствии с условием микроскопической обратимости вероятности pij должны удовлетворять условиям:

Рij=exp() Pji=exp() и (1.16)

Обычно полагают, что при
Uj ? Ui Pji = wi (1.17)
И при Uj >Ui Рij = wi exp[-(Uj - Ui)/kT]
Где wi - вероятность появления некоторой конфигурации при случайном выборе (с использованием последовательности равномерно распределенных случайных чисел). Используя центральную предельную теорему теории вероятностей может быть доказано [17], что рассматриваемая цепь Маркова задает распределение, асимптотически стремящееся к каноническому.

На практике алгоритм Метрополиса реализуют следующим образом. Пусть заданы потенциал взаимодействия, конфигурация системы (начальное расположение частиц в элементарной ячейке моделирования) и температура Т. Рассчитывают потенциальную энергию системы Ui и вносят случайное изменение в конфигурацию (случайным образом выбирают к - ю частицу в ячейке и смещают ее). При этом энергия системы становится равной Uj. Если Uj < Ui, то считают, что система перешла в новое состояние. Если Uj < Ui, то сравнивают величину exp() со случайным числом оє(0,1). Если о? exp[-(Uj - Ui)/kT], то считают, что система перешла в j-е состояние. Если же о> exp[-(Uj - Ui)/kТ ], то переход в новое состояние не происходит, к - я частица сохраняет свои прежние координаты [18]. При этом j-ую конфигурацию в цепи не учитывают, а рассматривают прежнее расположение частиц, соответствующее энергии U Таким образом, чем больше значение энергии имеет система при случайном изменении конфигурации, тем с меньшей вероятностью она переходит в это состояние.
Очевидно, что расчет средних значений сопряжен с большим количеством вычислений, выполнение которых стало возможным только при появлении быстродействующих ЭВМ[19].
Одно из преимуществ метода Монте-Карло состоит в том, что алгоритм легко адаптировать к любому статистическому ансамблю. Например, при моделировании системы в NPT-ансамбле необходимо периодически изменять объем ячейки, а в уравнении (1.17) вместо разности потенциальных энергий использовать разность энтальпий:
ДH = ДU + PДV - kТ ln(1+ДV/V)N, (1.18)
Где P - давление, V - объем ячейки, ДV - изменение объема ячейки.
Усредняя термодинамические функции по конфигурациям на равновесном участке цепи Маркова по уравнению (1.14), легко рассчитать конфигурационную энтальпию и мольный объем :
Нконф = <U> + P<V>, Vm = <V>NA/N (1.19)
Для расчета других термодинамических функций - изобарической теплоемкости СР, изотермической сжимаемости kT и коэффициента температурного расширения б, необходимо проводить моделирования системы при различающихся параметрах состояния, а затем находить конечные разности[20]. Оценку указанных термодинамических функций можно сделать и по результатам одного моделирования, используя флуктуационные формулы:

KT==),
==),
Для решения большинства задач вполне достаточно проведения вычислений в каноническом ансамбле. Однако если требуется, то можно использовать и большой канонический ансамбль [21, 22].
Похожие статьи
-
Общие теоретические положения метода Монте Карло Метод Монте Карло, применяемый в статистической физике, является частным случаем общего метода...
-
Методы исследований электронной и пространственной структуры наноразмерных кластеров Квантовохимические методы исследования Все современные методы...
-
Нестандартный метод сильной связи (НМСС) - Метод Монте Карло в химическом моделировании
Предложенный в работе [4-5] вариант МСС, который назовем нестандартным МСС (НМСС), в отличие от стандартных МСС основан на другом выражении для...
-
Метод сильной связи - Метод Монте Карло в химическом моделировании
Для расчета энергии многоатомных систем имеются приближения трех уровней сложности: эмпирические [1-3], полуэмпирические [3-5] и первопринципные...
-
В настоящее время нельзя назвать область человеческой деятельности, в которой в той или иной степени не использовались бы методы моделирования. Особенно...
-
Датой рождения метода Монте-Карло принято считать 1949 г., когда появилась статья под названием "The Monte Carlo method". Создателями этого метода...
-
Одним из наиболее важных аспектов построения систем моделирования является проблема цели. Любую модель строят в зависимости от цели, которую ставит перед...
-
Важным для системного подхода является определение структуры системы -- совокупности связей между элементами системы, отражающих их взаимодействие....
-
Описание используемых методов - Моделирование вероятности банкротства
В данной работе было принято решение использовать логистический анализ с помощью пакета STATA, а также алгоритм CART с помощью SPSS Modeler. Бинарная...
-
В большинстве реальных больших систем не обойтись без учета "состояний природы" -- воздействий Стохастического типа, случайных величин или случайных...
-
Метод Монте-Карло используют для вычисления интегралов, в особенности многомерных, для решения систем алгебраических уравнений высокого порядка, для...
-
Обзор методов сильной связи - Метод Монте Карло в химическом моделировании
Различие стандартных МСС друг от друга заключается в основном в выборе формул, аппроксимирующих матричные элементы гамильтониана и энергию отталкивания в...
-
В соответствии со вторым законом термодинамики элементарный акт флотации возможен, если свободная энергия Е2 системы после закрепления частицы на...
-
Термодинамика. Химическая термодинамика. Термодинамические системы. Энергия. Внутренняя энергия Термодинамика изучает взаимное превращение теплоты,...
-
Основные понятия химической термодинамики - Химическая термодинамика. Термохимия. Решение задач
Прежде чем приступить к изучению предмета химической термодинамики, необходимо ввести ряд терминов и понятий, используемых в этом разделе. Изучаемые...
-
Наиболее ранним способом формализации экономико-математических и ТС является представление физических явлений с помощью систем дифференциальных...
-
Метод максимального правдоподобия - Основы научных исследований
Разработан Р. Фишером. Пусть Х 1 ,х 2 ...х N - выборка из генеральной совокупности случайной величины Х с функцией плотности вероятности Р(х, и),...
-
Пусть требуется разыграть испытания в каждом из которых событие А появляется с вероятностью р и не появляется с вероятностью 1-р [4]. Заменим...
-
Обобщенный метод наименьших квадратов - Моделирование в эконометрике
При наличии гетероскедастичности в остатках рекомендуется традиционный метод наименьших квадратов (МНК) заменять обобщенным методом наименьших квадратов...
-
В основе моделирования лежит теория подобия, которая утверждает, что абсолютное подобие может иметь место лишь при замене одного объекта другим точно...
-
Проникновение математики в экономическую науку связано с преодолением значительных трудностей. В этом отчасти была "по-винна" математика, развивающаяся...
-
С развитием системных исследований, с расширением экспериментальных методов изучения реальных явлений все большее значение приобретают абстрактные...
-
Заключение - Моделирование систем массового обслуживания с использованием метода Монте-Карло
Метод Монте-Карло можно определить как метод моделирования случайных величин с целью вычисления характеристик их распределений. Возникновение идеи...
-
Моделирование начинается с формирования предмета исследований -- системы понятий, отражающей существенные для моделирования характеристики объекта. Эта...
-
Введение - Основные методы и принципы моделирования в исследовании систем управления
В данной работе я попытаюсь раскрыть основные методы и принципы моделирования в разрезе исследования систем управления. Моделирование (в широком смысле)...
-
Модели и моделирование - Экономико-математические методы
Одним из основных методов научного познания является эксперимент, а самой распространенной его разновидностью - метод моделирования систем. В процессе...
-
Теоретическое обоснование математического моделирования - Математические методы и модели в экономике
Коммерческая деятельность в том или ином виде сводится к решению таких задач: как распорядиться имеющимися ресурсами для достижения наибольшей выгоды или...
-
Общие сведения Термодинамика - наука о превращениях энергии в различных процессах, как физических, так и химических, и о направлении процессов, о...
-
При написании программ численного интегрирования желательно, чтобы для любой функции распределение узлов являлось оптимальным или близким к нему. Однако...
-
Элементы матричного анализа - Методы решения системы линейных уравнений
Вектором, как на плоскости, так и в пространстве, называется направленный Отрезок , то есть такой Отрезок , один из концов которого выделен и называется...
-
Коалесцентный механизм элементарного акта наблюдается при флотации аполярных минералов с углеводородными маслами. По данному механизму частичка, на...
-
Общая схема метода Монте-Карло Сущность метода Монте-Карло состоит в следующем: требуется найти значение а некоторой изучаемой величины. Для этого...
-
Математическое ожидание, дисперсия Дискретной называют случайную величину, которая принимает отдельные, изолированные возможные значения с определенными...
-
Определение понятия "имитационное моделирование" - Имитационное моделирование в экономике
В современной литературе не существует единой точки зрения по вопросу о том, что понимать под имитационным моделированием. Так существуют различные...
-
Первое начало термодинамики. Энтальпия - Химическая кинетика, равновесия, термодинамика
Это закон сохранения энергии. Подводимая к системе теплота Q расходуется на изменение ее внутренней энергии и на совершение работы А: Q = U + А Здесь U =...
-
Для достижения поставленной цели предприятию требуются материалы, оборудование, энергия, рабочая сила и другие ресурсы. Каждое предприятие такими...
-
Решение задачи графическим методом - Математическое моделирование в менеджменте и маркетинге
Необходимо найти максимальное значение целевой функции L(x)= 2x1+2x2 > max, при системе ограничений: 6x1+8x2?48, (1) 8x1+11x2?88, (2)...
-
МЕТОДЫ ОСАЖДЕНИЯ, ИОННОГО ОБМЕНА, МЕМБРАННЫЕ МЕТОДЫ - Химические свойства и строение воды
Современные технологии позволяют изготавливать объемные или плоские фильтрующие материалы с однородными каналами практически любого размера. Мембранный...
-
Введение - Методы экономико-математического моделирования
Экономико-математическое моделирование является неотъемлемой частью любого исследования в области экономики. Бурное развитие математического анализа,...
-
Методы исследования математических моделей - Математическое моделирование в менеджменте и маркетинге
Все методы математического моделирования можно разделить на четыре класса: -аналитические (априорные); -имитационные (априорно-апостериорные) модели;...
Алгоритм Метрополиса - Метод Монте Карло в химическом моделировании