Условия оптимальности плана перевозок транспортной задачи. - Транспортная задача и ее решение методом потенциалов
Признак оптимальности плана перевозок T. З. устанавливает теорема.
Теорема. Для того, чтобы некоторый допустимый план X = (xij)m-nT. З. был оптимальным, необходимо и достаточно, чтобы ему соответствовала система из (m + n) чисел U1, U2, ..., Um ; V1, V2, ...Vn, удовлетворяющих условиям:
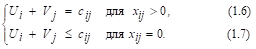
Числа Ui и Vj называются соответственно потенциалами пунктов отправления и пунктов назначения или потенциалами поставщиков и потребителей. А условия (1.6), (1.7) условиями оптимальности или потенциальности плана перевозок T. З..
Доказательство.
T. З., т. е. задачу нахождения минимума функции Z:
Xij ? 0, ; (1.1)
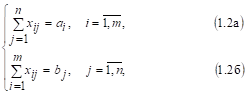
(1.2)
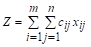
> min. (1.3)
Можно рассматривать как двойственную задачу к некоторой исходной прямой задаче линейного программирования (з. л.п.), условия которой легко получить по правилам построения двойственных задач. [ ]
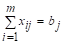
Каждому ограничению-равенству вида соответствует в прямой задаче свободная переменная Ui еа каждому ограничению-равенству вида соответствует в прямой задаче свободная переменная Vj.
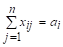
Каждой несвободной переменной xij ? 0, ; соответствует в прямой задаче ограничение-неравенство
Ui + Vj ? cij, ; (1.8)
Максимизируемой функцией прямой задачи является функция
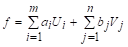
(1.9)
Задача (1.8), (1.9) в свою очередь является двойственной к T. З.. Теперь используя 1-ю и 2-ю теоремы двойственности докажем сформулированную теорему.
Необходимость. Пусть X = (xij) - оптимальный план T. З.. Поскольку оптимальный план является всегда допустимым, следовательно, он удовлетворяет условиям (1.1) и (1.2) T. З., т. е.
Xij ? 0, ; ;
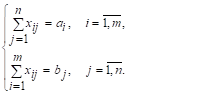
Согласно 1-й теореме двойственности прямая задача (1.8), (1.9) также имеет оптимальное решение U1, U2, ..., Um; V1, V2, ...Vn; удовлетворяющее условиям (1.8), т. е. Ui + Vj ? cij, ; и следовательно, условия (1.7) выполняются. По 2-й теореме двойственности оптимальные решения обеих задач удовлетворяют условиям дополняющей нежесткости:
Xij (Ui + Vj - cij) = 0.( ; )
Отсюда следует, что для xij > 0, Ui + Vj - cij = 0 или Ui + Vj = cij т. е. условия (1.6) выполняются.
Вторая группа условий
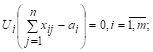
,
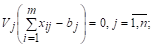
Выполняется автоматически, в силу условий (1.2).
Достаточность. Пусть для некоторого допустимого плана существует система чисел ; , удовлетворяющая условиям (1.6), (1.7). Выполнение этих условий означает, что эта система чисел является допустимым решением прямой задачи (1.8), (1.9) (условия (1.8) при этом будут выполняться). Выполнение условий (1.7) означает, что допустимое решение U1, U2, ..., Um; V1, V2, ...Vn прямой задачи и допустимый план двойственной задачи (T. З.) удовлетворяют условиям дополняющей нежесткости:
Xij (Ui + Vj - cij) = 0
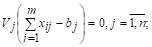
(вторая группа условий; выполняется автоматически).
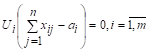
По 2-й теореме двойственности допустимый план является оптимальным. Теорема доказана.
Рассмотрим связь условий оптимальности (1.6) и (1.7) плана перевозок транспортной задачи с критерием оптимальности решения в симплексном методе.
Решим T. З. симплексным методом, одновременно найдем и оптимальное решение U1, U2, ..., Um; V1, V2, ...Vn задачи (1.8), (1.9). Вычислим оценки ?ij векторов :
?ij =Ui + Vj - cij, ; .
Транспортная задача является задачей на минимум и поэтому в симплекс-методе, критерий оптимальности решения для з. л.п. на минимум формируется так: если для данного опорного решения все оценки неположительны, то это опорное решение оптимально. Поэтому и для T. З. решение оптимально, если все оценки ?ij ? 0. При этом для всех базисных векторов :
?ij =Ui + Vj - cij,
Следовательно, для всех базисных переменных
Xij: Ui + Vj = cij
Т. е. получим условие (1.6).
Для небазисных векторов : ?ij =Ui + Vj - cij ? 0, т. е. для небазисных переменных xij:
Ui + Vj ? cij
Т. е. получили условие (1.7).
Из теоремы следует, что для того чтобы план T. З., записанный в таблице был оптимален, необходимо выполнение следующих условий:
- для каждой базисной клетки (i, j) сумма потенциалов должна быть равна соответствующему тарифу Cij: Ui + Vj = cij;
Если опорный план является вырожденным и какая-то из базисных переменных равна нулю, то для клетки, соответствующей этой переменной тоже должно выполняться условие Ui + Vj = cij;
- для каждой свободной клетки (i, j) сумма потенциалов должна быть меньше либо равна Cij: Ui + Vj ? cij или
Дij = Ui + Vj - cij ? 0.
Значения Дij являются оценками соответствующих свободных переменных xij; будем называть их оценками свободных клеток (i, j).
Для базисных клеток оценки Дij = Ui + Vj - cij = 0.
Вывод. Поскольку T. З. является задачей линейного программирования (з. л.п.) на минимум, то критерий оптимальности решения здесь формулируется так: если для данного опорного решения все оценки неположительны, то это решение оптимально. Если хотя бы одна из свободных клеток имеет положительную оценку, то опорный план оптимальным не является, и его можно улучшить, вводя в базис свободную переменную, соответствующую этой клетке.
Похожие статьи
-
Транспортная задача оптимальность Поставим в соответствие поставщикам потенциалы Ui, , а потребителям - Vj, . В оптимальном плане для всех базисных...
-
Теорема. Чтобы транспортная задача была разрешима, необходимо и достаточно, чтобы выполнялось условие: (1.5) Доказательство: Необходимость. Пусть...
-
Специфика транспортной задачи позволяет находить новое опорное решение задачи и новый базис по правилу более простому, чем в симплекс-методе. Пусть...
-
Ранг системы ограничений T. З. равен (m + n - 1), следовательно, невырожденный опорный план Т-задачи содержит (m + n - 1) положительных компонент или...
-
Транспортная задача (Т. З.) является одной из распространенных задач линейного программирования специального вида. Эта задача такого наиболее...
-
Вариант №1 1. Выбрать и обосновать наиболее эффективный метод решения задачи. 2. Разработать алгоритм и программу для решения задачи в общем виде. 3....
-
Пересчет симплекс-таблицы. - Транспортная задача
Формируем следующую часть симплексной таблицы. Вместо переменной x в план 1 войдет переменная x1 . Строка, соответствующая переменной x1 в плане 1,...
-
Методика решения задач ЛП графическим методом - Линейное программирование
I. В ограничениях задачи (1.2) заменить знаки неравенств знаками точных равенств и построить соответствующие прямые. II. Найти и заштриховать...
-
Математический аппарат Для понимания всего дальнейшего полезно знать и представлять себе геометрическую интерпретацию задач линейного программирования,...
-
Предложенный подход к решению задач исследования Используя в качестве основы присутствующее в наличии программное обеспечение, которое применимо к...
-
Постановка задачи: Для заданных функций необходимо: 1. Построить электронную таблицу (одну для обеих функций) для вычисления значений функций в заданном...
-
Транспортная задача - Линейное программирование
Одна из наиболее распространенных задач математического программирования -- транспортная задача. В общем виде ее можно представить так: требуется найти...
-
Геометрический метод, Двойственная задача - Линейное программирование
Применяется для задач с двумя переменными. Метод решения состоит в следующем: На плоскости строятся прямые, которые задают соответствующие ограничения:...
-
"РЕШЕНИЕ ЗАДАЧ ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ С ИСПОЛЬЗОВАНИЕМ MICROSOFT EXCEL" Цель работы Приобретение навыков решения задач линейного программирования...
-
Технические требования Техническое задание данной работы требует разработать программу для визуального редактирования HTML-кода. Программа должна быть...
-
Для реализации поставленной задачи методом конечных элементов будут использованы следующие программные обеспечения (ПО): - MATLAB - ПО и одноименный язык...
-
Варианты - Решение задач линейного программирования с использованием Microsoft Excel
Используя MS Excel, найти решение для модели ЛП, соответствующей заданному варианту (табл. 1.5). Таблица 1.5 Варианты задач к лабораторной работе № 1 №...
-
Методы Рунге-- Кутты-- важное семейство численных алгоритмов решения обыкновенных дифференциальных уравнений и их систем. Данные итеративные методы...
-
Для ускорения процесса конструирования регулятора в пространстве состояний в Matlab была разработана функция, которая, при должной настройке, позволяет...
-
Библиотека MSHTML MSHTML (так же известен как Trident) - браузерный движок для Microsoft Internet Explorer. Впервые Trident был реализован в четвертой...
-
Метод конечных элементов (МКЭ) жесткости возник в аэрокосмической отрасли. Исследователи рассматривали различные подходы к анализу сложных частей...
-
Задача многокритериальной оптимизации формально представляется как задача нелинейного программирования, включающая: процедуру анализа, выбор управляемых...
-
Входная информация разделяется на условно-постоянную и оперативно-учетную информацию. - Условно-постоянная информация включает в себя справочные данные о...
-
Выведем в общем виде уравнение движения заданной динамической модели при помощи уравнений Лагранжа II рода. Полная кинетическая энергия: , Полная...
-
Поиск информации В проектах этого типа учащиеся должны использовать различные источники информации (электронные или бумажные) для решения задач. Такой...
-
Для решения задачи №3 необходимо ввести исходные данные в электронную таблицу, т. е. таблицы 1,2 (рисунок 16). Рисунок 16 - Ввод исходных данных в...
-
Обобщенный алгоритм решения задачи Необходимо рассчитать сумму налога на дарение, воспользовавшись налоговой шкалой. Если сумма подарка менее 80, то она...
-
Анализ предметной области Описание ПО решаемой задачи Предметной областью задачи № 2 также является процесс оплаты денежных средств по кредиту. Решается...
-
На рисунке 1 представлен фрагмент электронной таблицы, в которой содержаться исходные данные для решения задачи. Рисунок 1 - Фрагмент электронной...
-
, Алгоритм обратного хода: Шаг 1. Вычислим Шаг 2. Вычислим: , Рис. 1. Основной алгоритм решения СЛУ методом исключения Гаусса. Для контроля правильности...
-
Транспортная задача - Транспортная задача
Сформулировать линейную производственную задачу и составить ее математическую модель, взяв исходные данные из приложения 1, где технологическая матрица А...
-
Дана система линейных уравнений (СЛУ) с n неизвестными: В матричной форме записи система (1) имеет вид: (2) Где : n - порядок системы; - матрица...
-
Обобщенный алгоритм решения задачи Необходимо рассчитать, какую сумму денежных средств внесет лицо, производящее оплату по 1 000 рублей ежеквартально под...
-
Введение - Программные и аналитические решения финансовых и экономических задач
Табличные процессоры - одно из важнейших средств для решения задач широкого назначения. Табличные процессоры в силу своей наполненности включены в пакет...
-
ЗАКЛЮЧЕНИЕ - Разработка электронного учебного пособия "VBA. Решение задач"
В результате дипломного проектирования было создано электронное учебное пособие "VBA. Решение задач" в соответствии требованием заказчика (преподаватель...
-
Аналитический способ решения задачи №3 представляет собой проверку вычислений: - для лица Лушников В. В. сумма налога на дарение составит 0, т. к. сумма...
-
Постановка задачи нечеткого управления Была рассмотрена задача по прогнозированию износа (в микрометрах) тормозных дисков автомобилей. Входные данные:...
-
Теоретическая основа линейного программирования, Симплекс метод - Линейное программирование
Симплекс метод Симплекс метод - метод линейного программирования, который реализует рациональный перебор базисных допустимых решений, в виде конечного...
-
Для создания наиболее совершенных и экономичных механизмов и машин важно получить оптимальный вариант входящих в них редукторов (МЗП). Показатель, на...
-
Постановка задачи На стадии оперативного управления возможна замена материалов и комплектующих, указанных в спецификациях, их аналогами. Аналогами...
Условия оптимальности плана перевозок транспортной задачи. - Транспортная задача и ее решение методом потенциалов