Транспортная задача - Транспортная задача
Сформулировать линейную производственную задачу и составить ее математическую модель, взяв исходные данные из приложения 1, где технологическая матрица А затрат различных ресурсов на единицу каждой продукции, вектор объемов ресурсов В и вектор удельной прибыли С при возможном выпуске четырех видов продукции с использованием трех видов ресурсов
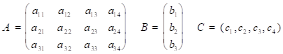
Компактно записаны в виде
C1 c2 c3 c4
А11 а12 а13 а14 b1
A21 a22 a23 a24 b2
A31 a32 a33 a34 b3
Преобразовать данную задачу к виду основной задачи линейного программирования, решить ее методом направленного перебора базисных допустимых решений, обосновывая каждый шаг процесса, найти оптимальную производственную программу, максимальную прибыль, остатки ресурсов различных видов и указать узкие места производства.
В последней симплексной таблице указать обращенный базис Q-1, соответствующий оптимальному набору базисных неизвестных. Проверить выполнение соотношения H = Q-1B
Если по оптимальной производственной программе какие-то два вида продукции не должны выпускаться, то в таблице исходных данных вычеркнуть соответствующие два столбца, составить математическую модель задачи оптимизации производственной программы с двумя оставшимися переменными, сохранив прежнюю нумерацию переменных и решить графически.
- 1.16 27 10 9 8 3 5 0 6 144 2 0 1 0 130 1 4 2 3 140
Задача имеет вид:
F(X) = 27x1 + 10x2 + 9x3 + 8x4 > max при ограничениях:
- 3x1 + 5x2 + 6x4?144 2x1 + x3?130
X1 + 4x2 + 2x3 + 3x4?140
Для приведения к канонической форме необходимо:
В 1-м неравенстве смысла (?) вводим базисную переменную x5. В 2-м неравенстве смысла (?) вводим базисную переменную x6. В 3-м неравенстве смысла (?) вводим базисную переменную x7.
- 3x1 + 5x2 + 0x3 + 6x4 + 1x5 + 0x6 + 0x7 = 144 2x1 + 0x2 + 1x3 + 0x4 + 0x5 + 1x6 + 0x7 = 130 1x1 + 4x2 + 2x3 + 3x4 + 0x5 + 0x6 + 1x7 = 140
F(X) = 27x1 + 10x2 + 9x3 + 8x4
Расширенная матрица системы ограничений-равенств данной задачи:
|
3 |
5 |
0 |
6 |
1 |
0 |
0 |
144 |
|
2 |
0 |
1 |
0 |
0 |
1 |
0 |
130 |
|
1 |
4 |
2 |
3 |
0 |
0 |
1 |
140 |
Поскольку в системе имеется единичная матрица, то соответствующие уравнения имеют вид:
- 3x1 + 5x2 + 6x4 + x5 = 144 2x1 + x3 + x6 = 130
X1 + 4x2 + 2x3 + 3x4 + x7 = 140
Выразим базисные переменные через остальные:
X = - 3x1 - 5x2 - 6x4 - x5+144
X = - 2x1 - x3 - x6+130
X = - x1 - 4x2 - 2x3 - 3x4 - x7+140
Подставим их в целевую функцию:
F(X) = 27x1 + 10x2 + 9x3 + 8x4
F(X) = 27x1 + 10x2 + 9x3 + 8x4 > max
Система неравенств:
- - 3x1 - 5x2 - 6x4 - x5+144 ? 0 - 2x1 - x3 - x6+130 ? 0 - x1 - 4x2 - 2x3 - 3x4 - x7+140 ? 0
Приводим систему неравенств к следующему виду:
- 3x1 + 5x2 + 6x4 + x5 ? 144 2x1 + x3 + x6 ? 130
X1 + 4x2 + 2x3 + 3x4 + x7 ? 140
F(X) = 27x1 + 10x2 + 9x3 + 8x4 > max
Упростим систему.
- 3x1 + 5x2 + 6x4 + x5 ? 144 2x1 + x3 + x6 ? 130
X1 + 4x2 + 2x3 + 3x4 + x7 ? 140
F(X) = 27x1 + 10x2 + 9x3 + 8x4 > max
Решим прямую задачу линейного программирования симплексным методом, с использованием симплексной таблицы.
Определим максимальное значение целевой функции F(X) = 27x1 + 10x2 + 9x3 + 8x4 при следующих условиях-ограничений.
- 3x1 + 5x2 + 6x4 + x5?144 2x1 + x3 + x6?130
X1 + 4x2 + 2x3 + 3x4 + x7?140
Для построения первого опорного плана систему неравенств приведем к системе уравнений путем введения дополнительных переменных (переход к канонической форме). В 1-м неравенстве смысла (?) вводим базисную переменную x8. В 2-м неравенстве смысла (?) вводим базисную переменную x9. В 3-м неравенстве смысла (?) вводим базисную переменную x10.
- 3x1 + 5x2 + 0x3 + 6x4 + 1x5 + 0x6 + 0x7 + 1x8 + 0x9 + 0x10 = 144 2x1 + 0x2 + 1x3 + 0x4 + 0x5 + 1x6 + 0x7 + 0x8 + 1x9 + 0x10 = 130 1x1 + 4x2 + 2x3 + 3x4 + 0x5 + 0x6 + 1x7 + 0x8 + 0x9 + 1x10 = 140
Матрица коэффициентов A = a(ij) этой системы уравнений имеет вид:
|
3 |
5 |
0 |
6 |
1 |
0 |
0 |
1 |
0 |
0 |
|
2 |
0 |
1 |
0 |
0 |
1 |
0 |
0 |
1 |
0 |
|
1 |
4 |
2 |
3 |
0 |
0 |
1 |
0 |
0 |
1 |
Базисные переменные это переменные, которые входят только в одно уравнение системы ограничений и притом с единичным коэффициентом.
Решим систему уравнений относительно базисных переменных:
X8, x9, x10,
Полагая, что свободные переменные равны 0, получим первый опорный план:
X1 = (0,0,0,0,0,0,0,144,130,140)
Базисное решение называется допустимым, если оно неотрицательно.
|
Базис |
B |
X1 |
X2 |
X3 |
X4 |
X5 |
X6 |
X7 |
X8 |
X9 |
X10 |
|
X8 |
144 |
3 |
5 |
0 |
6 |
1 |
0 |
0 |
1 |
0 |
0 |
|
X9 |
130 |
2 |
0 |
1 |
0 |
0 |
1 |
0 |
0 |
1 |
0 |
|
X10 |
140 |
1 |
4 |
2 |
3 |
0 |
0 |
1 |
0 |
0 |
1 |
|
F(X0) |
0 |
-27 |
-10 |
-9 |
-8 |
0 |
0 |
0 |
0 |
0 |
0 |
Переходим к основному алгоритму симплекс-метода.
Итерация №0.
1. Проверка критерия оптимальности.
Текущий опорный план неоптимален, так как в индексной строке находятся отрицательные коэффициенты.
2. Определение новой базисной переменной.
В качестве ведущего выберем столбец, соответствующий переменной x1, так как это наибольший коэффициент по модулю.
3. Определение новой свободной переменной.
Вычислим значения Di по строкам как частное от деления:bi / ai1
И из них выберем наименьшее:
Min (144:3 , 130:2 , 140:1) = 48
Следовательно, 1-ая строка является ведущей.
Разрешающий элемент равен (3) и находится на пересечении ведущего столбца и ведущей строки.
|
Базис |
B |
X1 |
X2 |
X3 |
X4 |
X5 |
X6 |
X7 |
X8 |
X9 |
X10 |
Min |
|
X8 |
144 |
3 |
5 |
0 |
6 |
1 |
0 |
0 |
1 |
0 |
0 |
48 |
|
X9 |
130 |
2 |
0 |
1 |
0 |
0 |
1 |
0 |
0 |
1 |
0 |
65 |
|
X10 |
140 |
1 |
4 |
2 |
3 |
0 |
0 |
1 |
0 |
0 |
1 |
140 |
|
F(X1) |
0 |
-27 |
-10 |
-9 |
-8 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
Похожие статьи
-
Пересчет симплекс-таблицы. - Транспортная задача
Формируем следующую часть симплексной таблицы. Вместо переменной x в план 1 войдет переменная x1 . Строка, соответствующая переменной x1 в плане 1,...
-
Теорема. Чтобы транспортная задача была разрешима, необходимо и достаточно, чтобы выполнялось условие: (1.5) Доказательство: Необходимость. Пусть...
-
Математический аппарат Для понимания всего дальнейшего полезно знать и представлять себе геометрическую интерпретацию задач линейного программирования,...
-
Теоретические аспекты поставленной задачи В этой части проекта будут объяснены этапы применения МКЭ для плоской фермы. В первой главе было рассмотрено...
-
Геометрический метод, Двойственная задача - Линейное программирование
Применяется для задач с двумя переменными. Метод решения состоит в следующем: На плоскости строятся прямые, которые задают соответствующие ограничения:...
-
Постановка задачи Основной целью дипломной работы является создание комплексной системы информационной безопасности предприятия на примере информационной...
-
Постановка задачи Имеющаяся база данных SQL имеет недостаточное количество полей и таблиц, не имеет упорядоченной структуры пользователей для работы с...
-
Решение задач линейного программирования - Основы информатики
Имеются n пунктов производства и m пунктов распределения продукции. Стоимость перевозки единицы продукции с i-го пункта производства в j-ый центр...
-
Транспортная задача оптимальность Поставим в соответствие поставщикам потенциалы Ui, , а потребителям - Vj, . В оптимальном плане для всех базисных...
-
Вариант №1 1. Выбрать и обосновать наиболее эффективный метод решения задачи. 2. Разработать алгоритм и программу для решения задачи в общем виде. 3....
-
Варианты - Решение задач линейного программирования с использованием Microsoft Excel
Используя MS Excel, найти решение для модели ЛП, соответствующей заданному варианту (табл. 1.5). Таблица 1.5 Варианты задач к лабораторной работе № 1 №...
-
Языки и системы программирования, их эволюция - Автоматизация решения задач пользователя
Язык программирования - это способ записи программ решения различных задач на ЭВМ в понятной для компьютера форме. Процессор компьютера непосредственно...
-
Введение. - Приложения технологии системы электронных таблиц Excel к решению задач механики
История развития программ обработки электронных таблиц насчитывает немногим более десяти лет, но налицо значительный прогресс в области разработки такого...
-
Проектирование модели данных - Создание аналога системной утилиты "Диспетчер задач"
При проектировании модели данных разработаем диаграмму вариантов использования, диаграмму деятельности. Диаграмма вариантов использования представляет...
-
Формулировка задачи - Линейное программирование
Даны линейная функция Z=С1 х1 +С2 х2 +...+СN xN (1.1) И система линейных ограничений A11 x1 + a22 x2 +... + a1N ХN = b1 A21 x1 + a22 x2 +... + a2N ХN =...
-
Построение модели предметной области с помощью описания структур данных и программного кода является классическим подходом в разработке ИС. Зачастую...
-
Ранг системы ограничений T. З. равен (m + n - 1), следовательно, невырожденный опорный план Т-задачи содержит (m + n - 1) положительных компонент или...
-
Аналитический способ решения задачи №3 представляет собой проверку вычислений: - для лица Лушников В. В. сумма налога на дарение составит 0, т. к. сумма...
-
Введение - Программные и аналитические решения финансовых и экономических задач
Табличные процессоры - одно из важнейших средств для решения задач широкого назначения. Табличные процессоры в силу своей наполненности включены в пакет...
-
Для того, чтобы разработать оптимальный метод интеграции сторонних систем в существующую ИТ-инфраструктуру систем компании, требуется точно поставить...
-
Предложенный подход к решению задач исследования Используя в качестве основы присутствующее в наличии программное обеспечение, которое применимо к...
-
Заключение. - Приложения технологии системы электронных таблиц Excel к решению задач механики
Целью курсовой работы являлось изучение полного спектра функциональных возможностей технологии системы электронных таблиц Excel. - Задачами данной работы...
-
Анализ существующих недостатков в информационном обеспечении управления, передаваемыми ООО "СЕРВИС ПАРТНЕР" позволяет констатировать наличие потребности...
-
Широкое распространение в операционной системе Windows имеет множество стандартных программ обеспечивающих работу устройств компьютера и служащих для...
-
Смысл таблицы - отображение строк и столбцов. Одинаковый тип данных по столбцам. Полосы прокрутки как по вертикали так и по горизонтали. Перемещение...
-
Как наука информатика имеет одну главную цель - применение ВМ для поиска нового знания. Собственной целью информатики является знание о знании, структуре...
-
Постановка задачи: Для заданных функций необходимо: 1. Построить электронную таблицу (одну для обеих функций) для вычисления значений функций в заданном...
-
Связь типов информационных систем с задачами принятия решений - Системы поддержки принятия решений
Применяются отдельные модели и методы для принятия оптимальных решений. Отметим, что в существенной мере характер всех поколений систем и их концепций...
-
Распределение задач между процессами - Администрирование параллельных процессов
Распределение подзадач между процессорами является завершающим этапом разработки параллельного метода. Надо отметить, что управление распределением...
-
ТЕОРЕТИЧЕСКОЕ ОБОСНОВАНИЕ ЗАДАЧИ, Строковый тип данных в языке Pascal - Строковый тип данных
Строковый тип данных в языке Pascal Познакомимся с типом данных, который относится к числу структурированных. Это строковый тип данных (строка). Строка -...
-
Признак оптимальности плана перевозок T. З. устанавливает теорема. Теорема. Для того, чтобы некоторый допустимый план X = (xij)m-nT. З. был оптимальным,...
-
При создании или при классификации информационных систем неизбежно возникают проблемы, связанные с формальным - математическим и алгоритмическим...
-
Базы данных (БД) составляют в настоящее время основу компьютерного обеспечения информационных процессов, входящих практически во все сферы человеческой...
-
Формирование области многокритериального выбора вариантов Стоит задача о выборе марки автомобиля с их известными особенностями и характеристиками....
-
Заключение - Сравнение моделей представления слов в задаче очистки текста от обесцененной лексики
В данной работе проводится сравнение эффективности 6 методов поиска по однословному запросу. В качестве запроса выступает слов из стоп-листа - списка...
-
Постановка задачи Необходимо разработать программу для поиска автобусных маршрутов. В качестве среды разработки должна использоваться Delphi 7. В...
-
Для создания наиболее совершенных и экономичных механизмов и машин важно получить оптимальный вариант входящих в них редукторов (МЗП). Показатель, на...
-
Табличный процессор Excel фирмы Microsoft предназначен для ввода, хранения, обработки и выдачи больших объемов, данных в виде, удобном для анализа и...
-
Выполнения проекта монтажа охранной сигнализации состоит из множества операций, которые складываются в этапы работ проекта. Схематично структура этапов...
-
Операционная система Windows XP была разработана и выпущена на смену операционной системе DOS фирмой Microsoft XP в 2002 году. Именно поэтому она и...
Транспортная задача - Транспортная задача