Конструирование функционала - Проблемы конструирования устойчивой системы автоматического управления
Основная часть алгоритма - не связанная с математическими сложностями вычисления решений уравнений Риккати и Винера-Хопфа - заключается в составлении правильного функционала и решении задачи с его помощью.
Так как было установлено, что функционалы (2.7) и (2.9) не позволяют решить поставленную задачу, возникает вопрос о там как именно стоит их модифицировать, чтобы сконструированный регулятор обладал стабилизирующим свойством.
Для того, чтобы разрешить проблему, мы проанализируем свойства, которыми должен быть обладать регулятор, дополним функционал в операторной постановке задачи и приведем способ его перевода в постановку пространства состояний. Используя полученные выводы можно будет провести сравнительную оценку практического хода решения задачи в обоих пространствах, а также проверить составленные функционалы на адекватность относительно желаемых свойств сконструированной системы (глава 3).
Вернемся к постановке задачи. Нам требуется построить линейный квадратичный регулятор, который бы:
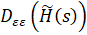
A) обеспечивал минимум воспроизведения задающего воздействия, т. е. минимизировал,
B) обладал стабилизирующим свойством.
Первое условие уже учитывается в базовом функционале в обоих постановках. Рассмотрим техническую сторону второго требования. Стабилизирующий регулятор должен обеспечивать свойство устойчивости в системе. Систему мы считаем устойчивой, если она обладает этим свойством по начальным условия и по входу. Заметим, что - на основании критериев - устойчивость по начальным условиям следует из устойчивости системы по входу - так как указанное имеет место при устойчивости характеристического полинома системы. Таким образом регулятор должен обеспечить две вещи:
A) устойчивость характеристического полинома системы,
B) свою строгую реализуемость.
Строгая реализуемость регулятора обеспечивается второй составляющей критерия (2.9). Чтобы
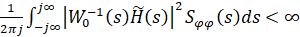
Необходимо, чтобы степень полиномов в числителе элементов матрицы как минимум не превосходила степени полиномов в знаменателе.
Для устойчивости характеристического полинома системы необходимо и достаточно, чтобы все его корни имели отрицательную действительную часть. В случае, если построенный регулятор компенсирует находящиеся на мнимой оси нули или полюса объекта управления, полином становится неустойчивым, так как у него появляются корни, не удовлетворяющие критерию.
Рассмотрим одномерный случай. Запишем характеристического уравнение нашей замкнутой системы:
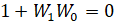
Тогда, полагая
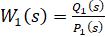
,
Запишем уравнение для поиска корней характеристического полинома:
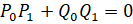
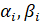
Пусть - находящиеся на мнимой оси и компенсируемые построенным регулятором нули и полюса объекта управления, тогда:
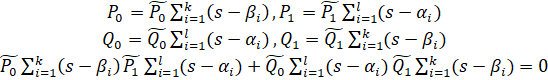
Отсюда
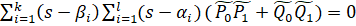
Как мы видим, если регулятор компенсирует находящиеся на мнимой оси нули или полюса управляющего объекта, они автоматически станут корнями характеристического полинома системы и, как результат, мы получим неустойчивую систему.
Таким образом нам необходимо дополнить функционал (2.9) таким образом, чтобы он исключал возможность возникновения рассмотренной выше ситуации.
Заметим, что критерий (2.9) уже ограничивает возможность компенсации нулей управляющего устройства. Вторая его составляющая
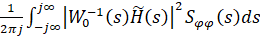
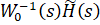
Конечна, если не имеет полюсов на мнимой оси. Таким образом ограничение на компенсацию регулятором правых нулей объекта управления уже учтено как в пространстве операторов, так и в пространстве состояний. Проверим это утверждение для одномерного случая:
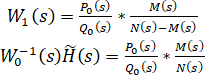
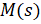
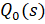
Из условия сходимости оценки должен компенсировать лежащие на мнимой оси нули полинома. Как итог - они не попадут в знаменатель.
Итак, было установлено, что функционал необходимо пополнить условием, которое бы ограничивало компенсацию регулятором мнимых полюсов устройства управления.
Для избавления от возникающей негрубости системы можно ввести в функционал (2.9) с малым весом оценку для следующего выражения:
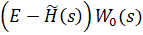
(2.11)
Для ограниченности ее оценки, т. е.
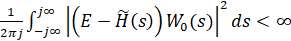
(2.12)
Необходимо, чтобы полюса выражения (2.11) не лежали на мнимой оси. Обратимся к одномерному случаю:


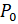
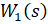
Сформулированное выше условие выполняется, если компенсирует мнимые нули. И на основе выражения для из (2.8) можно утверждать, что введение оценки (2.12) в функционал (2.9) обеспечит ограничение на компенсацию регулятором мнимых полюсов устройства управления.
Приведем модифицированный функционал:
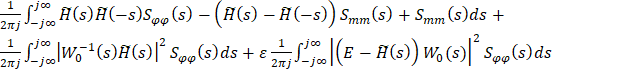
(2.13)
Реализовать в пространстве состояний оценку (2.12) можно с помощью переменных состояния - расширением пространства, либо с помощью воздействия вида белого шума.
Чтобы перевести добавку (2.12) на язык пространства состояний первым способом необходимо будет ввести набор переменных, которые будут реализовывать (на основе уже имеющегося вектора состояний)
.
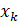
В итоге у нас будет переменная, такая что:
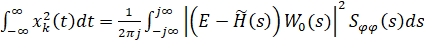
Более подробно данный вопрос будет рассмотрен в главе 3.
К сожалению, было установлено, что перевод функционала (2.13) в пространстве изображений с помощью расширения вектора состояний не дал желаемого результата - полученный регулятор не обладал стабилизирующим свойством.
Обратимся ко второму способу - использованию воздействия вида белого шума. Некоторые составляющие интегрального критерия могут быть реализованы в пространстве состояний с помощью введения фиктивного воздействия. Рассмотрим (1.6). Для ее реализации в постановке нашей задачи необходимо подать на вход объекта белый шум единичной интенсивности.
Приведем схему подобного устойства:
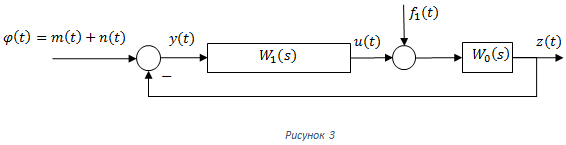
Подобное фиктивное воздействие приведет к тому, что функционал примет вид:
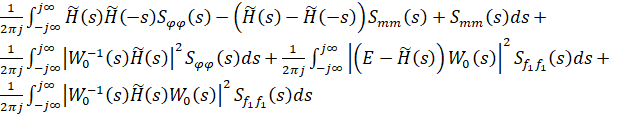
(2.14)
Последняя составляющая обусловлена вкладом вводимой помехи в сигнал управления.
Приведем вывод этой оценки. Для этого найдем передаточную функцию от входа к выходу :
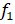
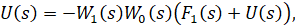
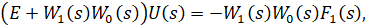
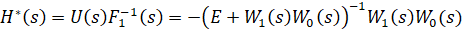
Теперь выразим :
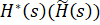
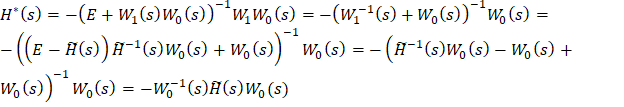
Теперь вклад сигнала в управление можно оценить:
Похожие статьи
-
Заключение - Проблемы конструирования устойчивой системы автоматического управления
Управление алгоритм фильтрация устойчивость В настоящей работе была проанализирована проблема оптимальной стабилизирующей фильтрации для класса объектов...
-
Для ускорения процесса конструирования регулятора в пространстве состояний в Matlab была разработана функция, которая, при должной настройке, позволяет...
-
Обзор классического подхода Приведем теорему для формирования линейного закона управления с обратной связью в пространстве состояний [3]: Дан объект,...
-
Воспользуемся теперь критерием (2.14). Пространство состояний Структурная схема системы с учетом введенного воздействия примет вид: Запишем...
-
Воспользуемся теперь для поиска решения функционалом (2.13). Пространство операторов В рассматриваем примере добавка (2.12) может быть представлена:...
-
Введение - Проблемы конструирования устойчивой системы автоматического управления
Теория автоматического управления - молодая наука, оформившаяся в самостоятельную общенаучную дисциплину в начале XX века. Истоки ее инженерных методов...
-
На ней - квадратная матрица передаточных функций объекта управления с полюсами и нулями на мнимой оси. - матрица передаточных функций фильтра,...
-
Рассмотрим произвольное звено коррекции: (1.5) Соотношение между и обусловлено требованием строгой реализуемости проектируемого звена как необходимого...
-
При формулировании задачи в одном из пространств возникает необходимость перехода к тождественной постановки в другом. К сожалению, не всегда...
-
Устойчивость - Проблемы конструирования устойчивой системы автоматического управления
Перейдем от общих понятий к формализации данного свойства в интересующей нас сфере. В случае нестационарных систем существует множество различных...
-
Приведем некоторые оценки, линейные комбинации которых используются в качестве обобщенного интегрального критерия при решении задач в пространстве...
-
Проблема управляемости - это ликвидация начального рассогласования [4]. Рассматривается это понятие через программное управление (поиск управления как...
-
Линейная замкнутая система Рассмотрим линейную стационарную непрерывную управляемую систему: (1.1) - вектор состояния системы, - управление, - выход...
-
В настоящей главе будет произведен разбор частного случая задачи оптимальной фильтрации. На примере будет разобран ход построения алгоритма, будут...
-
Для разделения действительной и мнимой частей передаточной функции умножим числитель и знаменатель передаточной функции на комплексно сопряженное число...
-
Сформулируем задачу поиска оптимального регулятора в общих понятиях: дан многомерный реальный объект управления с квадратной матричной передаточной...
-
Ввиду неточности определений характеристик управляемого объекта, неполноты его описания, наличия возмущений различного рода, деградаций самой элементной...
-
Программа контроллера была разработана в специализированной программной среде TwinCAT фирмы BECKHOFF. Пакет программного обеспечения BECKHOFF TwinCAT...
-
В дипломном проекте была проделана следующая работа: - Выбрана элементная база для стенда. Согласно заданию стенд спроектирован на основе промышленного...
-
Пожаром называют неконтролируемое горение во времени и пространстве, наносящее материальный ущерб и создающее угрозу жизни и здоровью людей. В...
-
В настоящее время стала очень актуальна проблема разработки, проектирования и создания "умных" зданий. Умные здания помогают более эффективнее и...
-
Задача оптимальной фильтрации заключается в конструировании устройства, отфильтровывающий полезный сигнал от помехи. Приведем схему для множества...
-
После рассмотрения достоинств и недостатков информационных систем, автоматизирующих управление персоналом, можно перейти к проведению оценки соответствия...
-
Котроллеры на основе блока CPU BC9120, в принципе как и на основе любого другого блока CPU фирмы BECKHOFF, построены по модульному принципу. Что это...
-
Датчики выбираются согласно техническому заданию и следующим критериям: - наличие унифицированных выходных сигналов 4-20мА - доступная цена - компактные...
-
Учебно-демонстрационный стенд "Система автоматического управления инженерными системами помещения" создается по нескольким причинам. Во-первых, в связи...
-
Конструкция учебно-демонстрационного стенда Стенд представляет собою имитацию двухэтажного здания. На панели управления расположены следующие органы...
-
Рисунок 5.6.1 - Общий вид программы визуализации. Все переключатели и кнопки находящиеся на передней панели управления стендом дублируются одноименными...
-
Вариант 14 Преобразовать структурную схему и найти передаточную функцию системы автоматического управления по управляющему воздействию. Рисунок 1.1.1...
-
Объявление переменных VAR {программные переменные} HL8_1,{включение HL8 с генератора случайных чисел в режиме "охрана"} HL9_1,{включение HL9с генератора...
-
Под нажатием кнопки понимается нажатие кнопки на стенде или одноименной кнопки в программе визуализации, аналогично для переключателей. Под срабатыванием...
-
Конфигурация "Управление производственным предприятием" является современной многооконной системой. Каждое из ее окон (многие из которых -- диалоговые...
-
Считается, что правильно организованный документооборот и электронный архив документов становятся необходимыми условиями эффективной работы современного...
-
Основная цель системы ДИСКОР - совершенствование оперативного управления работой железных дорог на основе более эффективного использования пропускной...
-
Если линейная система устойчива, то ее переходная функция будет с течением времени стремиться к постоянному значению, а весовая функция - к нулю....
-
На закладке Товары оформляется поступление тех видов номенклатуры, которые являются товарами или материалами (рис.6). Именно по списку номенклатуры этой...
-
Для всех операций документа "Реализация товаров и услуг" она выглядит одинаково и предназначается для оформления отгрузки возвратной тары (рис. 23). Рис....
-
Для разработки принципиальной электрической схемы, исходя из задания и выбранной элементной базы, составим структурную схему стенда, которая будет иметь...
-
Исходя из технических характеристик входных/выходных модулей, модуля CPU и датчиков приведенных выше, понадобится 2 блока питания с питающим напряжением...
-
Планировка и организация рабочего места должна основываться на учете антропометрических и психофизиологических данных людей. Рабочее место должно...
Конструирование функционала - Проблемы конструирования устойчивой системы автоматического управления