Центрально-симметрическое поле звезды и движение материи - Геометрическая турбулентность и эволюция звезд
Будем рассматривать эволюцию звезд в рамках модифицированной теории Эйнштейна [23-24]. Уравнения гравитационного поля Эйнштейна имеют вид:
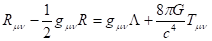
(24)
- тензор Риччи, метрический тензор и тензор энергии-импульса; - космологическая постоянная Эйнштейна, гравитационная постоянная и скорость света соответственно.
В общем случае имеют место соотношения
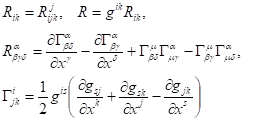
(25)
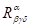
- тензор Римана, - символы Кристоффеля второго рода.
Тензор энергии-импульса материи в уравнении (24), вообще говоря, зависит от гравитационного поля. Чтобы сохранить основную идею определения метрики в теории гравитации Эйнштейна, мы предположим, что уравнение Эйнштейна (1) распадается на два независимых уравнения [23-24]:
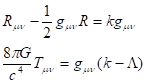
(26)
Здесь - некоторая функция, зависящая от размерности пространства. Отметим, что первым уравнением определяется метрика пространства-времени, а вторым уравнением задается распределение материи, которое соответствует этой метрике. Эта гипотеза соответствует идее о происхождении материи из гравитационного поля [35], но без специального предположения о наличии сингулярности метрики.
В работе [24] представленная модель квантовой гравитации в многомерных пространствах размерностью с метрикой
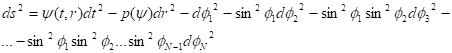
(27)
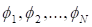
Здесь - углы на единичной сфере, погруженной в мерное пространство. Метрика (27) описывает многие важные случаи симметрии, используемые в физике элементарных частиц. Такой подход позволяет охватить все многообразие материи, путем выбора уравнения состояния.
Рассмотрим гравитацию в пространствах с метрикой (27). Уравнение Эйнштейна в форме (26) является универсальным, поэтому обобщается на пространство любого числа измерений. Движение материи будем описывать уравнением Гамильтона-Якоби, которое также обобщается на любое число измерений. Вместе эти два уравнения составляют универсальную модель, описывающую движение материи в - мерном пространстве:
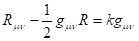
(28)
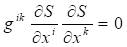
(29)
Уравнения поля в метрике (27) сводятся к одному уравнению второго порядка [24]
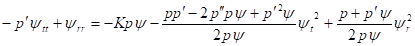
(30)
В общем случае параметры модели и скалярная кривизна зависят только от размерности пространства, имеем
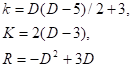
(31)
Отметим, что уравнение (30) изменяет свой тип в зависимости от знака производной :
В области уравнение (30) имеет эллиптический тип;
В области уравнение (30) имеет гиперболический тип;
В области уравнение (30) имеет параболический тип.
Уравнение Гамильтона-Якоби в метрике (27) имеет вид
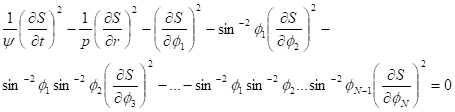
(32)
Уравнение (32) можно проинтегрировать при некоторых предположениях, используя метод, который предложил Шредингер [36]. Суть метода состоит в том, чтобы представить решение уравнения (32) в виде
(33)
Здесь в теорию в явном виде вводится классическое действие - , постоянная Планка и волновая функция. Используя классическое действие, мы определяем те параметры задачи, которые могут считаться внешними для квантовой системы. В случае метрики (27) удобно будет выбрать в качестве переменных квантовой механики углы на единичной сфере, а в качестве координат классического действия - время и радиальную координату. Тогда уравнение (32) разделяется на два уравнения
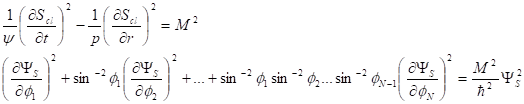
(34)
Здесь - произвольная постоянная.
Рассмотрим гравитационные волны, которые возникают в метрике (27) в случае линейного уравнения состояния. Положим в уравнении (30)
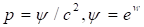
.
Тогда уравнение (30) приводится к виду уравнения Лиувилля:
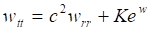
(35)
Отметим, что уравнение (35) широко используется в теории струн и квантовой гравитации [25-26, 39-40]. Для уравнения (35) можно указать общее решение [37-38]:
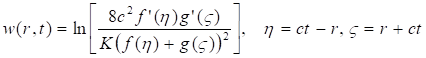
(36)
Здесь - произвольные функции.
Используя формулу Лиувилля (36), можно указать общее решение уравнений Эйнштейна в форме (26), описывающее гравитационные волны в метрике (27):
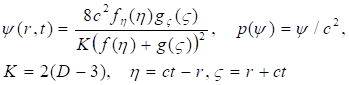
(37)
Гравитационные волны типа (37) распространяются в комбинации, включающей опережающие и запаздывающие волны. Следовательно, скалярные гравитационные волны могут служить источником квантового движения частиц, например, в форме волн де Бройля [24].
Действительно, запишем первое уравнение (34) в метрике (27), учитывая (37) имеем
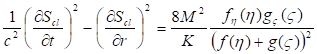
(38)
Предполагая, что действие зависит от координат, преобразуем обе части уравнения (38) к эквивалентному виду
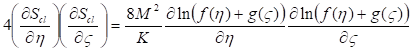
(39)
Отсюда следует, что действие можно выразить через произвольные функции в виде
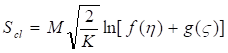
(40)
Уравнение (40) можно рассматривать и в обратную сторону, предполагая, что неизвестные функции связаны с действием пробных частиц адрон частица звезда турбулентность
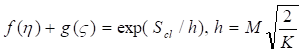
(41)
Все функции, входящие в уравнение (41) являются вещественными.
Далее предположим, что
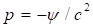
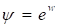
, (42)
Тогда приходим к уравнению Лиувилля эллиптического типа
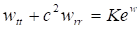
(43)
В этом случае также можно получить решения уравнения (43) общего вида, которые выражаются через аналитические функции [37-38]. Отметим, что уравнение Лиувилля эллиптического типа широко применяется в теории горения и равновесия звезд [1, 4]. Применение эллиптической модели (43) в квантовой теории гравитации можно найти в работе [26].
В статическом случае уравнение (30) приводится к виду
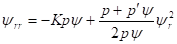
(44)
Интегрируя уравнение (45), получим
(45)
Здесь С - произвольная постоянная. Для моделирования метрики типа (2) в теории Эйнштейна-Янга-Миллса, зависящей от двух периодов рассмотрим уравнение состояния в форме
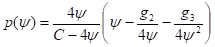
(46)
Общее решение уравнения (45) с уравнением состояния (46) выражается через функцию Вейерштрасса
(47)
Если существует движение в плоскости в четырехмерном пространстве-времени, то метрика (27) и уравнение поля (30) принимают вид
(48)
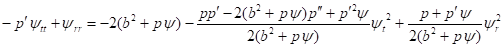
(49)
Здесь - параметр движения. В статическом случае уравнение (49) можно проинтегрировать один раз, в результате получим
(50)
Положим в уравнении (50)
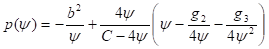
(51)
Тогда вновь приходим к метрике (47), зависящей от функции Вейерштрасса. Такого рода зависимость центрально-симметрической метрики от функции Вейерштрасса приводит к значительному расслоению вещества по плотности, что и наблюдается в природе. Так, например, атом имеет плотное ядро и электронные оболочки. Наша планета содержит ядро, мантию, литосферу, атмосферу и магнитосферу. В строении Солнца также предполагается наличие плотного ядра, зоны лучистого переноса, конвективной зоны, фотосферы и атмосферы, состоящей из хромосферы, переходной зоны, короны и гелиосферы.
Похожие статьи
-
Уравнения гравитационного поля Эйнштейна имеют вид [4-8]: (1) - тензор Риччи, метрический тензор и тензор энергии-импульса; - космологическая постоянная...
-
Основные уравнения модели метрики адронов - Геометрическая турбулентность и эволюция звезд
Рассмотрим центрально-симметричную метрику вида [9-14] (1) Здесь - метрический тензор пространства Минковского сигнатуры (- + + +), - гауссова кривизна...
-
Эволюция звезд и геометрическая турбулентность - Геометрическая турбулентность и эволюция звезд
Используем полученные результаты для доказательства того, что горение вещества в звездах обусловлено только изменением метрики пространства-времени....
-
Динамика частиц - Геометрическая турбулентность и эволюция звезд
Кварки и преоны представляют собой частицы-фермионы, обладающие спином Ѕ и дробным электрическим зарядом - смотрите таблицы 1-2. Для описания динамики...
-
Метрика пузыря - Геометрическая турбулентность и эволюция звезд
В метрике (2) можно определить дефект решетки типа пузыря. В области пузыря считаем, что, а во внешней области решение зададим в виде (2), имеем (4) На...
-
Введение - Геометрическая турбулентность и эволюция звезд
Вопрос об источнике энергии звезд обсуждался в работах [1-7] и других. В одной из первых моделей эволюции звезд [1] предполагалось, что вещество...
-
Модель нуклонов - Геометрическая турбулентность и эволюция звезд
Влияние векторного потенциала на параметры барионов исследовалось в работе [12]. Было установлено, что масштаб изменения параметров векторного поля...
-
Модель кварков и лептонов - Геометрическая турбулентность и эволюция звезд
Используем полученные результаты для вычисления магнитных моментов электрона и кварков. Общие свойства исследуемых частиц представлены в таблицах 1-2. С...
-
Литература - Геометрическая турбулентность и эволюция звезд
Emden R. Gaskugeln: Leipzig, Germany: Teubner, 1907; The Internal Constitution of the Stars// Die Naturewissenschaften, V. 15, Issue 38, pp. 769-776,...
-
Покажем, что для любой классической системы, обладающей центральной симметрией и заданной энергией, существует такая метрика, что действие системы будет...
-
Введение - Аномальное движение орбит в общей теории относительности
Как известно, в общей теории относительности можно определить аномальное движение орбит [1]. Для решения задачи о вековом аномальном смещении перигелия...
-
Рождение и эволюция отдельных типов звезд - Общие сведения о звездах и их типологии
Процесс звездообразования. Эволюция звезд -- это изменение со временем физических характеристик, внутреннего строения и химического состава звезд....
-
Схема рождения Вселенной., Возникновение и эволюция звезд - Астрономическая картина мира
Возбужденный вакуум, сжатый до состояния точки. Быстрое расширение - инфляция. Через 10-32 с. Холодная и пустая Вселенная размером в несколько...
-
Астрофизика (физика звезд на поздней стадии эволюции) - Еще раз о Мироустройстве
Из выступления директора Государственного астрономического ин-та им. Штейнберга, академика РАН, профессора, Черепащук. Черные Дыры, Кротовые Норы, Темная...
-
Аномальные радиальные колебания орбит - Аномальное движение орбит в общей теории относительности
В общем случае уравнения движения материальной точки в гравитационном поле имеют вид [3,6,11-12] (39) Вычисляя коэффициенты аффинной связности в метрике...
-
Общее решение уравнений относительного движения - Математическое моделирование движения небесных тел
Рассмотрим на небесной сфере сферический треугольник N M x, где M - проекция текущего положения тела M на небесную сферу. Сторонами этого треугольника...
-
Уравнение Бине - Математическое моделирование движения небесных тел
Другой способ получения траектории движения в задаче двух тел связан с широко известным уравнением Бине. Это уравнение записывается в цилиндрической...
-
4.1 Введение В предыдущих главах было подробно изучено промежуточное движение искусственного спутника. Была рассмотрена качественная картина движения,...
-
Понятие эволюции звезды - Эволюция и строение звезд
Эволюция звезда гравитационное сжатие Эволюция звезд - изменение физических характеристик, внутреннего строения и химического состава звезд со временем....
-
Жизненный цикл звезд зависит от их массы: звезды с низкой массой в конечном итоге превращаются в белых карликов, в то время как жизнь звезд с большой...
-
Введение - Эволюция и строение звезд
Подавляющее большинство звезд меняет свои основные характеристики (светимость, радиус) очень медленно. В каждый данный момент их можно рассматривать как...
-
Заключение - Эволюция и типы звезд
Звезды эволюционируют, и их эволюция необратима, так как все в природе находится в состоянии беспрерывного изменения. Внешние характеристики звезды...
-
Происхождение звезд - Рождение и эволюция звезд
Сейчас установлено, что звезды и звездные скопления имеют разный возраст, от величины порядка 1010 лет (шаровые звездные скопления) до 106 лет для самых...
-
Эволюция звезд малой массы ( до 8 М Солнца) - Строение и эволюция звезд и планет
Если массы, необходимой для начала термоядерной реакции, недостаточно (0,01-0,08 масс Солнца), термоядерные реакции никогда не начнутся. Такие...
-
В основу всех современных гипотез о происхождении планет положена идея о формировании их из газопылевого облака. При этом большинство ученых склоняется к...
-
ВСТУПЛЕНИЕ - Строение и эволюция звезд и планет
Вопросы, связанные со строением Вселенной, волновали человечество еще до появления самого понятия Вселенная. Ученые античности, средневековья, а за ними...
-
Образование и эволюция звезд - Образование и эволюция звезд
Звезды - наиболее распространенные объекты во Вселенной. Более 98% массы наблюдаемого космического вещества сосредоточено в них. Эволюция звезд - важный...
-
Строение и эволюция Вселенной - Происхождение и развитие галактик и звезд
Вселенная бесконечна во времени и пространстве. Каждая частичка вселенной имеет свое начало и конец, как во времени, так и в пространстве, но вся...
-
Механизм образования и эволюции звезд - Рождение и эволюция звезд
Согласно современным представлениям, звезды возникают в результате гравитационного сжатия плотных газопылевых облаков с последующим разогревом и...
-
"Рождение звезды" - Особенность эволюции звезд
Эволюция звезды начинается в гигантском молекулярном облаке (звездная колыбель). Молекулярное облако имеет плотность около миллиона молекул на см3. Масса...
-
Черные дыры. - Эволюция и типы звезд
Если масса звезды в два раза превышает солнечную, то к концу своей жизни звезда может взорваться как сверхновая, но если масса вещества оставшегося после...
-
Основные характеристики и эволюция звезд
В результате огромной работы, проделанной астрономами ряда стран в течение последних десятилетий, мы многое узнали о различных характеристиках звезд,...
-
Нейтронные звезды и пульсары, Черные дыры - Происхождение и эволюция звезд
"Остатки взорвавшегося ядра известны под названием нейтронной звезды. Нейтронные звезды вращаются очень быстро, испуская световые и радиоволны, которые,...
-
Нейтронные звезды, Черные дыры - Эволюция звезд
Известно, что в некоторых сверхновых сильная гравитация в недрах сверхгиганта заставляет электроны поглотиться атомным ядром, где они, сливаясь с...
-
Стадии звездной эволюции - Эволюция и строение звезд
Этот процесс является закономерным, то есть неизбежным. В самом деле, тепловая неустойчивость межзвездной среды неизбежно ведет к ее фрагментации, то...
-
Как и все тела в природе, звезды не остаются неизменными, они рождаются, эволюционируют, и наконец "умирают". Чтобы проследить жизненный путь звезд и...
-
Полученные дифференциальные уравнения для элементов промежуточной орбиты позволяют довольно просто построить аналитическую теорию движения спутника со...
-
Параболическое движение, Прямолинейное движение - Математическое моделирование движения небесных тел
(p = 0, e = 1) Уравнение параболической орбиты записывают в видеp r = 1 + cos v (1.80) Где величина определяет расстояние от центра притяжения M0 до...
-
Введение, Темная Материя во Вселенной - Поиски Темной материи
Мы стоим на пороге открытия, способного изменить суть наших представлений о Мире. Речь идет о природе темной материи. Из анализа многих экспериментальных...
-
В этой части мы сведем дифференциальные уравнения (2.1.6) к квадратурам, которые и будут в дальнейшем использованы для построения промежуточной орбиты...
Центрально-симметрическое поле звезды и движение материи - Геометрическая турбулентность и эволюция звезд