Метрика пузыря - Геометрическая турбулентность и эволюция звезд
В метрике (2) можно определить дефект решетки типа пузыря. В области пузыря считаем, что, а во внешней области решение зададим в виде (2), имеем
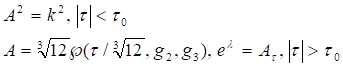
(4)
На границах пузыря непрерывна функция и ее первая производная,
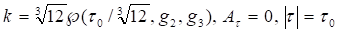
(5)
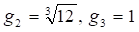
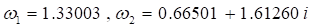
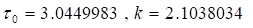
Положим, тогда полупериоды функции Вейерштрасса определяются в виде. Отсюда находим первый ноль и соответствующее значение параметра метрики.
Отметим, что метрика во внутренней области пузыря является трехмерной, поскольку не содержит радиальной координаты. Действительно, используя уравнения (1) и (4), находим
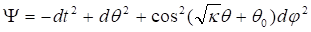
(6)
Аналогично строится решение для других корней второго уравнения (5). Все эти решения отличаются только размером пузыря, тогда как значение параметра не меняется.
Всякий пузырь можно вывернуть наизнанку, просто изменив на противоположные неравенства (4). В этом случае можно доопределить метрику во внешней области пузыря, используя решение первого уравнения (2), так, чтобы метрика внешнего пространства совпала с метрикой нашей Вселенной [11]. Наконец, третий тип частиц можно составить как комбинацию двух первых, в результате возникает пузырь, ограниченный оболочкой конечной толщины.
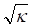
Преобразуем метрику (6) к стандартному виду. Для этого умножим обе части выражения (6) на постоянное число и введем новые переменные, отличающиеся от старых переменных на постоянный множитель, в результате находим
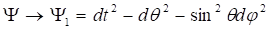
(7)
Метрика (7) использовалась для моделирования структуры барионов [12-13], в том числе протона и нейтрона. Наконец, заметим, что результаты работ [20-22] и других, касающихся динамики преонов в метрике типа (1)-(2), носят гипотетический характер, так как сам факт существования преонов еще не установлен. Ниже приведены основные результаты по динамике частиц, полученные в наших работах [12-14, 20-22].
Похожие статьи
-
Модель кварков и лептонов - Геометрическая турбулентность и эволюция звезд
Используем полученные результаты для вычисления магнитных моментов электрона и кварков. Общие свойства исследуемых частиц представлены в таблицах 1-2. С...
-
Динамика частиц - Геометрическая турбулентность и эволюция звезд
Кварки и преоны представляют собой частицы-фермионы, обладающие спином Ѕ и дробным электрическим зарядом - смотрите таблицы 1-2. Для описания динамики...
-
Будем рассматривать эволюцию звезд в рамках модифицированной теории Эйнштейна [23-24]. Уравнения гравитационного поля Эйнштейна имеют вид: (24) - тензор...
-
Основные уравнения модели метрики адронов - Геометрическая турбулентность и эволюция звезд
Рассмотрим центрально-симметричную метрику вида [9-14] (1) Здесь - метрический тензор пространства Минковского сигнатуры (- + + +), - гауссова кривизна...
-
Модель нуклонов - Геометрическая турбулентность и эволюция звезд
Влияние векторного потенциала на параметры барионов исследовалось в работе [12]. Было установлено, что масштаб изменения параметров векторного поля...
-
Эволюция звезд и геометрическая турбулентность - Геометрическая турбулентность и эволюция звезд
Используем полученные результаты для доказательства того, что горение вещества в звездах обусловлено только изменением метрики пространства-времени....
-
Введение - Геометрическая турбулентность и эволюция звезд
Вопрос об источнике энергии звезд обсуждался в работах [1-7] и других. В одной из первых моделей эволюции звезд [1] предполагалось, что вещество...
-
Литература - Геометрическая турбулентность и эволюция звезд
Emden R. Gaskugeln: Leipzig, Germany: Teubner, 1907; The Internal Constitution of the Stars// Die Naturewissenschaften, V. 15, Issue 38, pp. 769-776,...
-
Введение - Эволюция и строение звезд
Подавляющее большинство звезд меняет свои основные характеристики (светимость, радиус) очень медленно. В каждый данный момент их можно рассматривать как...
-
Рождение и эволюция отдельных типов звезд - Общие сведения о звездах и их типологии
Процесс звездообразования. Эволюция звезд -- это изменение со временем физических характеристик, внутреннего строения и химического состава звезд....
-
Стадии звездной эволюции - Эволюция и строение звезд
Этот процесс является закономерным, то есть неизбежным. В самом деле, тепловая неустойчивость межзвездной среды неизбежно ведет к ее фрагментации, то...
-
Эволюция на основе ядерных реакций - Эволюция и строение звезд
При температуре в ядрах ~ 106 К начинаются первые ядерные реакции - выгорают дейтерий, литий, бор. Первичное количество этих элементов настолько мало,...
-
Образование звезд, стадия гравитационного сжатия - Эволюция и строение звезд
Согласно наиболее распространенной точке зрения, звезды образуются в результате гравитационной конденсации вещества межзвездной среды. Необходимое для...
-
В основу всех современных гипотез о происхождении планет положена идея о формировании их из газопылевого облака. При этом большинство ученых склоняется к...
-
ВСТУПЛЕНИЕ - Строение и эволюция звезд и планет
Вопросы, связанные со строением Вселенной, волновали человечество еще до появления самого понятия Вселенная. Ученые античности, средневековья, а за ними...
-
Конечные стадии эволюции звезд
Конечные стадии эволюции звезд Сверхновые звезды - это массивные звезды, светимость которых внезапно увеличивается до огромной величины, а затем...
-
Магнитное поле звезд, Пузырь звездного ветра - Физика звезд
Звездное магнитное поле -- Магнитное поле , создаваемое движением проводящей Плазмы внутри звезд Главной последовательности . Это движение создается...
-
Строение звезд - Эволюция звезд
Звезды не останутся вечно такими же, какими мы их видим сейчас. Во Вселенной постоянно рождаются новые звезды, а старые умирают. Чтобы понять, как...
-
Основные характеристики и эволюция звезд
В результате огромной работы, проделанной астрономами ряда стран в течение последних десятилетий, мы многое узнали о различных характеристиках звезд,...
-
Звезды среднего размера - Эволюция звезд
При достижении звездой средней величины (от 0,4 до 3,4 солнечных масс) фазы красного гиганта в ее ядре заканчивается водород и начинаются реакции синтеза...
-
Нейтронные звезды, Черные дыры - Эволюция звезд
Известно, что в некоторых сверхновых сильная гравитация в недрах сверхгиганта заставляет электроны поглотиться атомным ядром, где они, сливаясь с...
-
Рождение и эволюция звезд - Рождение и эволюция звезд
Мир звезд огромен и разнообразен. За тысячи лет до нас это знали внимательные наблюдатели неба -- пастухи, мореходы, проводники караванов. Они отличали...
-
Поздние годы и гибель звезд, Старые звезды с малой массой - Эволюция звезд
Старые звезды с малой массой На сегодняшний день достоверно неизвестно, что происходит с легкими звездами после истощения запаса водорода. Поскольку...
-
Понятие эволюции звезды - Эволюция и строение звезд
Эволюция звезда гравитационное сжатие Эволюция звезд - изменение физических характеристик, внутреннего строения и химического состава звезд со временем....
-
Жизненный цикл звезд зависит от их массы: звезды с низкой массой в конечном итоге превращаются в белых карликов, в то время как жизнь звезд с большой...
-
Изобилие легких элементов - Концепция большого взрыва. Механизм образования и эволюции звезд
Ранняя Вселенная была очень горячей. Даже если протоны и нейтроны при столкновении объединялись и формировали более тяжелые ядра, время их существования...
-
Введение - Эволюция и типы звезд
Изучение естествознания нужно не только для того, чтобы мы как культурные люди знали и разбирались в его результатах, но и для понимания самой структуры...
-
Нейронные звезды. - Эволюция и типы звезд
Звезды, у которых масса в 1,5-3 раза больше, чем у Солнца не смогут в конце жизни остановить свое сжатие на стадии белого карлика. Мощные силы гравитации...
-
Сверхновые. - Эволюция и типы звезд
Около семи тысяч лет назад в отдаленном уголке космического пространства внезапно взорвалась звезда, сбросив с себя наружные слои вещества. Сравнительно...
-
Старые звезды с малой массой Поскольку возраст вселенной составляет 13,7 миллиардов лет, что недостаточно для истощения запаса водородного топлива в...
-
"Разновидности масс тел", Молодые звезды малой массы - Особенность эволюции звезд
Молодые звезды малой массы Это еще по сути протозвезды, в центре которых только начинаются ядерные реакции, и все излучение происходит, в основном, из-за...
-
Введение - Особенность эволюции звезд
Вселенная состоит на 98% из звезд. Они же являются основным элементом галактики. Звезда-- небесное тело, в котором идут в данный момент термоядерные...
-
Галактика - Происхождение и эволюция звезд
За пределами Млечного пути космос наполнен и другими галактиками, многие из которых составляют скопления из сотен и даже тысяч членов. Типы галактик...
-
Эволюция звезд - Происхождение и эволюция звезд
"Строение звезды и источник ее энергии казались в какой-то степени выясненными, но возникли другие, не менее важные вопросы. Так, оказалось, что Солнце,...
-
Эволюция звезд - Эволюция и типы звезд
Более девяти десятых вещества нашей планеты Галактики сосредоточено в звездах; есть галактики, в которых на звезды приходится 99,9% массы. Мир звезд...
-
Эволюция звезд - Рождение и эволюция звезд
Современная астрономия располагает большим количеством аргументов в пользу утверждения, что звезды образуются путем конденсации облаков газопылевой...
-
ЗАКЛЮЧЕНИЕ, СПИСОК ИСПОЛЬЗОВАННОЙ ЛИТЕРАТУРЫ - Строение и эволюция звезд и планет
В связи с прогрессом в развитии науки и техники, мы получили возможность заглянуть за пределы Солнечной системы, узнать многое о звездах, удаленных от...
-
Эволюция звезд - Космические тела
Как и все тела в природе, звезды не остаются неизменными, они рождаются, эволюционируют, и, наконец "умирают". Чтобы проследить жизненный путь звезд и...
-
Звезды, у которых масса в 1,5-3 раза больше, чем у Солнца не смогут в конце жизни остановить свое сжатие на стадии белого карлика. Мощные силы гравитации...
-
Как и все тела в природе, звезды не остаются неизменными, они рождаются, эволюционируют, и, наконец "умирают". Чтобы проследить жизненный путь звезд и...
Метрика пузыря - Геометрическая турбулентность и эволюция звезд