Улучшения классических силовых алгоритмов - Визуализация графа цитирования
Первым улучшением является добавление псевдо-гравитационной силы [11]. Эта сила притягивает все вершины к центру рабочей области. Обычно она линейна относительно расстояния, в отличие от обыкновенной гравитационной силы которая является обратно-квадратичной. Эта сила позволяет решить сразу две проблемы; первая - это то, что она стягивает граф в видимую область и не позволяет ему "уехать" за ее грани во время симуляции, вторая - это то, что она не дает несвязанным подграфам удалиться слишком далеко от центра.
Вторым улучшением является добавление силы трения [11]. Эта сила также является псевдо-силой в том понимании, что она не соответствует силе трения в реальном мире. Обычно она действует линейно на скорость уменьшая ее в определенное количество раз на каждом шаге алгоритма. Тем самым она позволяет не разгоняться вершинам слишком быстро, что часто бывает проблемой при работе подобных алгоритмов.
Также стоит упомянуть два метода, один из которых позволяет улучшить точность симуляции, а второй уменьшить ее вычислительную сложность.
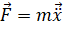
Для того, чтобы описать метод, улучшающий точность симуляции, необходимо поговорить о том, как проводилась симуляция согласно алгоритмам выше. Согласно алгоритмам выше на каждой итерации алгоритма высчитывалась суммарная сила алгоритма, умножалась на маленький коэффициент шага и добавлялась к позиции вершины. Однако, как известно из школьной физики, по второму закону Ньютона от силы линейно зависит не положение, а ускорение. Для того, чтобы найти положение нам нужно решить дифференциальное уравнение, хотя бы численно.
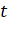
Самый простой способ решения - это воспользоваться методом Эйлера [12]. Он не сильно отличается от того, что мы делали раньше. Теперь для каждой вершины вводится понятие скорости, равной изначально 0. На каждом шаге мы вначале находим скорость как:
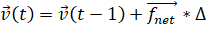
,
И только после этого вычисляем новые координаты:
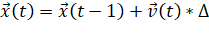
.
Этот метод работает лучше описанного Eades, однако он крайне неэффективен и нестабилен, так как он требует очень маленького шажка, а значит и их количества для хорошей точности, иначе ошибка будет быстро расти.
Поэтому чаще всего используют более сложный способ интегрирования - интегрирование Верле [13]. На каждом шаге, вначале высчитывается положение для следующего момента времени:
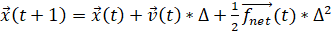
,
Далее считается скорость:
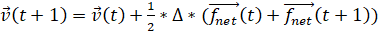
.
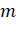
Если есть информация о массе вершины, то сила заменяется на ускорение:
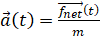
.
Этот метод более стабильный, чем метод Эйлера и позволяет использовать больший шаг.
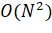
Теперь необходимо сказать о сложности алгоритма расположения вершин. На каждом шаге алгоритма для каждой из N Вершин необходимо посчитать силы, действующие на нее со стороны остальных N-1 Вершин. Соответственно вычислительная сложность на каждом шаге. Такой алгоритм будет медленно работать даже на сравнительно небольших графах, что неприемлемо для real-time задач и ухудшает user experience.
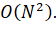
Для решение данной проблемы используется алгоритм аппроксимации симуляции динамической системы Барнса-Хата [14]. Он позволяет выполнить симуляцию за вместо Этот алгоритм используется полностью на каждом шаге симуляции.
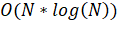
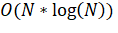
Первый шаг алгоритма Барнса-Хата - это построение квадродерева. Квадродерево рекурсивно делит рабочую область на 4 квадрата, называемых "квадрантами", пока внутри не будет нуля или одной вершины. Тес самым мы получаем дерево, в котором каждый узел - это квадрант и имеет 4 потомка (пример дерева на рис. 2). Сложность построения такого квадродерева. Во время построения дерева считается центр масс и масса каждого узла из всех объектов в его поддереве.
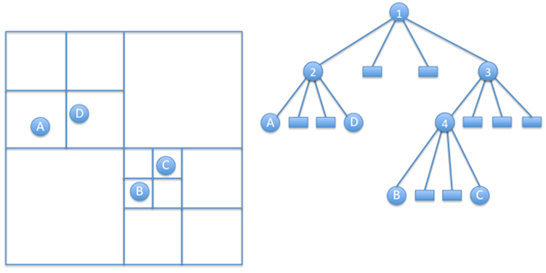
Рисунок 2. Квадродерево из 4 точек. Слева - разбиение плоскости на квадранты, справа - представление точек и квадрантов в виде дерева
Далее для каждого тела в симуляции высчитывается суммарная сила. Для этого начинается проход квадродерева, если центр масс текущего узла достаточно далек от тела, то мы представляем этот узел как большое тело с центром в центре масс и массой равной суммарной массе, и считаем силу, действующую на текущее тело со стороны узла. После этого потомки узла уже не просматриваются. Если же в какой-то ветке квадродерева мы не нашли такого узла, то мы доходим то листьев и считаем силу, действующую с их стороны.
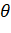
Узким местом этого алгоритма является понятие "достаточно далеко". Для его определения вводится эмпирический параметр. Если он больше отношения ширины узла к расстоянию от тела до центра масс узла, то узел считается "достаточно далеким". Фактически параметр позволяет управлять балансом между точностью и скоростью аппроксимации. Если имеет большое значение, то алгоритм будет работать быстро но с плохой точностью, а если близка к 0, то наоборот.
Похожие статьи
-
Силовые алгоритмы расположения вершин на плоскости - Визуализация графа цитирования
Классический подход к решению таких задач это использовать алгоритм из семейства силовых. Основная идея таких алгоритмов - это рассматривать графы как...
-
Существующие решения - Визуализация графа цитирования
На данный момент не было найдено решений, которые полностью бы удовлетворяли всем требованиям, однако существуют те, которые реализуют их не все и/или не...
-
Постановка задачи - Визуализация графа цитирования
В качестве результата выпускной квалификационной работы требуется создать программу, позволяющую визуализировать граф цитирования публикаций, которые...
-
Программа задания случайных графов Эрдеша - Реньи - Алгоритмы нескольких махов
Программа реализует алгоритм задания случайных графов Эрдеша - Реньи. В качестве входных параметров задаются число вершин и число ребер. Вершины ребер...
-
Автоматическое расположение вершин на плоскости - Визуализация графа цитирования
Первая проблема, о которой стоит поговорить - это проблема автоматического расположения вершин на плоскости. Для начала поставим базовую задачу, как она...
-
Обзор предметной области, Графы цитирования - Визуализация графа цитирования
Графы цитирования Во время работы над научными статьями и проектами возникает необходимость хранить используемые публикации. Стандартный поход к этой...
-
Введение - Визуализация графа цитирования
В данной работе рассматриваются методы автоматической и полуавтоматической визуализации графов цитирования на плоскости. Визуализация графов на плоскости...
-
Алгоритма LBFS+ достаточно для трехмахового алгоритма распознавания единичных интервальных графов, но для случая интервальных графов необходимы...
-
Программа реализует алгоритм четырех махов. Входным параметром является имя файла. На выходе печать: является ли граф единичным интервальным,...
-
Работа алгоритма LBFS начинается с заданной вершины графа, которая в общем случае выбирается случайно. Получаемый порядок вершин также может быть основан...
-
Для проведения тестов была написана программа задания единичного интервального графа. Входные параметры: число вершин, длина отрезка на котором задается...
-
Программные модули проекта, Представление графа в памяти ЭВМ - Алгоритмы нескольких махов
Все программы были реализованы на языке С++ на персональной ЭВМ с операционной системой Windows. Каждая программа представляет собой консольное...
-
Некоторые сведения из теории графов - Алгоритмы нескольких махов
Приведенные ниже определения взяты из [1,2,7-9], теоремы из [6]. Граф, или обыкновенный граф G -- это упорядоченная пара G := (V, E), где V -- это...
-
Итерационные алгоритмы разрезания графа на куски
Лекция Итерационные алгоритмы разрезания графа на куски Суть Итерационных Алгоритмов Разрезания Графов заключается в выборе первого случайного разрезания...
-
Стек технологий При выборе стека технологий основное внимание уделялось следующим факторам, в порядке убывания значимости: § Кроссплатформенность; §...
-
Теоретические аспекты поставленной задачи В этой части проекта будут объяснены этапы применения МКЭ для плоской фермы. В первой главе было рассмотрено...
-
ДВОИЧНЫЙ ПОИСК, АВЛ-Дерево - Структуры и алгоритмы обработки данных
Алгоритм двоичного поиска в упорядоченном массиве сводится к следующему. Берем средний элемент отсортированного массива и сравниваем с ключом X. Возможны...
-
Данный алгоритм (англ. Maximal Neighborhood Search - MNS) [7] в отличие от алгоритма BFS позволяет дополнительно упорядочить вершины в найденных...
-
Для вычисления цвета могут быть использованы различные подходы. Вычисление цвета может проводиться одновременно с геометрической реконструкцией,...
-
Для создания трехмерной реконструкции сцены или объекта необходимо создать его трехмерную модель и вычислить цвет ее вершин. Для геометрической...
-
Численные эксперименты были проведены для следующих целей: Подтверждение корректности алгоритмов. Подтверждение линейности временных затрат алгоритмов. В...
-
Обоснование выбранного метода При дизайне системы согласно требованиям или при оптимизации существующей необходимо ввести модель, позволяющую не только...
-
Входные параметры: входной файл, выходной файл, номер вершины, номер вершины. Если задаваемые номера вершин положительные, то добавляется соответствующее...
-
Алгоритмы распознавания интервальных и единичных интервальных графов [2,5-7] основываются на специальном упорядочивании вершин графа и проверке...
-
Каскадный классификатор - Исследование алгоритмов
В настоящее время метод Виолы-Джонса является самым популярным методом для детектирования в силу своей высокой скорости и эффективности. В 2001 году П....
-
В работе возникает необходимость выбора предметной области, в которой будет тестироваться каскадный классификатор. Главными вопросами на данном этапе...
-
Для упрощения работы с трехмерной моделью на любом этапе проектирования и повышения ее наглядности в SolidWorks используется Дерево Построений (Feature...
-
Модификации алгоритма Лемпеля-Зива, предложенная Терри Уэлчем - Анализ алгоритма Лемпеля-Зива
В 1984 году Терри Уэлч (Terry Welch) предложил адаптивный сброс словаря для алгоритма LZ78 [3]. В этом случае при заполнении словаря сброс словаря не...
-
В алгоритме Zhou&;Koltun при вычислении отклонений цвета используется изображение, переведенное в градации серого. В данной реализации используется...
-
Введение - Алгоритмы нескольких махов
Теория графов в последнее время широко используется в различных отраслях науки и техники, особенно в экономике и социологии, а также в генетике,...
-
Идея алгоритма Лемпеля-Зива, Алгоритм LZ77 - Анализ алгоритма Лемпеля-Зива
Основная идея алгоритма Лемпеля-Зива состоит в замене появления фрагмента в данных (группы байт) ссылкой на предыдущее появление этого фрагмента....
-
В этом разделе намеренно допущено отступление от общей методики - не смешивать разные компоненты. Это сделано для облегчения демонстрации построения...
-
Приложение, которое необходимо разработать, должно производить геометрическую реконструкцию сцены и вычисление цвета вершин модели. Для геометрической...
-
ОСОБЕННОСТИ РЕАЛИЗАЦИИ АЛГОРИТМОВ - Структуры и алгоритмы обработки данных
В ходе выполнения курсовой работы, помимо основных алгоритмов, потребовалось реализовать также несколько вспомогательных, необходимых для корректной...
-
Постановка задачи Необходимо разработать программу для поиска автобусных маршрутов. В качестве среды разработки должна использоваться Delphi 7. В...
-
Поворот точки относительно центра на заданный угол: X = o. X + (p. X-o. X) * cos(angle) - (p. Y-o. Y) * sin(angle) Y = o. Y + (p. X-o. X) * sin(angle) +...
-
Обзор классического подхода Приведем теорему для формирования линейного закона управления с обратной связью в пространстве состояний [3]: Дан объект,...
-
Свойства алгоритмов - Алгоритм
Данное выше определение алгоритма нельзя считать строгим - не вполне ясно, что такое "точное предписание" или "последовательность действий,...
-
Примеры визуального представления данных - Визуализация количественных данных
Визуализация программный обеспечение данные В научно-технической документации применяются различные виды визуализации (ниже приведены примеры...
-
Введение - Исследование алгоритмов
С недавнего времени такая область кибернетики, как создание искусственных систем распознавания образов, стала представлять особый интерес. Потребность в...
Улучшения классических силовых алгоритмов - Визуализация графа цитирования