Методологічні та програмно-алгоритмічні особливості розв'язання обернених задач - Прямі та обернені задачі гравіметрії в класі блочно побудованих геологічних моделей
Розглянуто можливості методу підбору з точки зору отримання надійних розв'язків в умовах широкої еквівалентності. Показано, що властивості розв'язків, отримуваних методом підбору, значною мірою визначаються прийнятою апроксимацією геологічного середовища. Якщо геологічне середовище апроксимувати цілісними блоками з постійною густиною, встановлюючи лише їх конфігурацію (що спрощує обчислення при аналітичному описі та забезпечує мінімальну кількість параметрів), то вплив еквівалентності на розв'язок задачі значно послаблюється. При заданих обмеженнях на шукані параметри можна отримати еквівалентну модель, якщо ж сформовано клас єдиності, то розв'язок, як показує практика, буде однозначним і залежатиме лише від моделі початкового наближення. Стійкість розв'язку визначається ефективністю алгоритму мінімізації цільової функції.
Встановлення області збіжності для конкретного модельного класу досліджувалося раніше теоретично (Є. Г. Булах, М. М. Маркова, Т. Л. Міхеєва), проте практична реалізація можлива лише за значних модельних спрощень. Без встановлення області збіжності функціоналу в результаті підбору може бути отриманий довільний еквівалентний розв'язок, залежно від вибору вихідної точки. В цій ситуації доцільним видається визначення множини еквівалентних розв'язків та подальший її аналіз з урахуванням наявної апріорної інформації та змістовних обмежень на шукані параметри.
Запропонований Алгоритм околів дозволяє отримувати множину еквівалентних моделей. Ідея алгоритму належить австралійському вченому М. Самбріджу, і виникла у зв'язку з розв'язанням сейсмічних обернених задач. Алгоритм околів грунтується на апроксимації параметричного простору функцією нев'язки, яка визначається для кожної точки простору. Для цього використовуються геометричні конструкції відомі під назвою діаграм Вороного. Оскільки кожній точці параметричного простору можна поставити у відповідність значення функції нев'язки даних, і навколо цієї точки єдиним чином можна визначити комірку Вороного, то апроксимація модельного простору здійснюється простим встановленням постійної нев'язки всередині кожної комірки. У такий спосіб D-Вимірний модельний простір єдиним чином поділяється на області (випуклі многогранники).
Сам алгоритм доволі простий і полягає в наступному:
- 1. Утворити початковий ряд моделей рівномірно (або в якийсь інший спосіб) розподілених у параметричному просторі. 2. Обчислити значення функції нев'язки для утвореного ряду моделей і визначити моделей, яким відповідають найменші нев'язки. 3. Утворити нових моделей, виконуючи рівномірний випадковий крок всередині комірки Вороного кожної з вибраних моделей (тобто, моделей в кожній комірці). 4. Перейти до п. 2.
Для того, щоб реалізувати алгоритм околу, не потрібно визначати всі елементи діаграми Вороного (що було б не розв'язуваною задачею). Як видно з рис. 2, досить лише знайти точки, в яких межі D-вимірної комірки Вороного перетинають I-у вісь, що проходить через точку А. Тоді наступна варіація рівномірного випадкового кроку обмежується двома точками на осі ( та на рис. 2). Визначення точок перетину осі з межами комірки можна здійснити виходячи з геометричних міркувань.
Нехай навколо моделі (вектора) сформовано K-у комірку Вороного. Точку, в якій границя між K-ю та J-ю комірками перетинає I-у вісь позначимо, тоді за означенням маємо
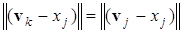
.
Приймаючи, що
,
Будемо мати
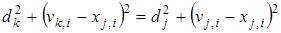
,
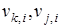
Де - проекції векторів та на I-у вісь відповідно; - відстань від точки до біжучої I-ї осі. З останнього рівняння отримуємо
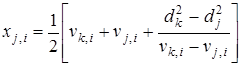
(2)
Для того, щоб знайти границі комірки Вороного, рівняння (2) має бути оцінено для всіх комірок і вибрано дві найближчі до А точки.
Більш формально, маємо нижню межу з умови
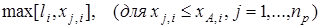
І верхню межу з умови
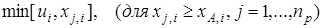
,
Де і - нижня і верхня межі параметричного простору в I-у напрямі відповідно.
Після здійснення циклу по всіх напрямах (координатах) створюється нова модель у параметричному просторі.
Серед інших особливостей алгоритму околів слід відзначити наступні. Наявність випадкових похибок у спостережених даних не впливає на результативність запропонованого алгоритму, оскільки функція нев'язки в даному випадку слугує не критерієм мінімізації, а є лише способом порівняння моделей. Алгоритм околів є стійким, оскільки в процесі його роботи не накопичуються обчислювальні похибки. Слід також відмітити, що при застосуванні алгоритму околів досліджується увесь параметричний простір, що виключає попадання процесу пошуку в локальний мінімум, тоді як при мінімізації функціоналу градієнтним методом найшвидшого спуску точка мінімуму залежить від початкової моделі і може виявитися точкою локального мінімуму. Результатом алгоритму околів є множина е - еквівалентних моделей, де е - наперед задана величина. Наочно продемонстровано дієвість алгоритму для дво - та тривимірного параметричного просторів.
Похожие статьи
-
Актуальність теми . Проблема розвитку ефективних методів пошуку та розвідки покладів корисних копалин завжди була актуальною для України, і особливої...
-
У вступі обгрунтовується актуальність теми роботи, формулюється мета та завдання дослідження, вказується наукова новизна отриманих результатів, їх...
-
Модели пластов и процесса вытеснения нефти [2,7,12,14] - Основы добычи нефти и газа
Под моделью в широком научном смысле этого слова понимают реально или мысленно созданную структуру, воспроизводящую или отражающую изучаемый объект....
-
Полученное, после регистрации 15 планшетов топографической карты масштаба 1 : 500 растровое поле о использовано для создания цифровой модели местности....
-
Показатели, близкие к реальным, получают в ряде случаев при расчете разработки нефтяных месторождений с помощью модели, состоящей из моделей процесса...
-
Гидродинамическая модель сработки грунтовых вод при предуборочном осушении рисовых чеков
Население Земли ежегодно растет, а следовательно, растут и потребности в сельскохозяйственных продуктах. Наибольшие темпы роста населения наблюдаются в...
-
Компьютерная обработка аэрокосмических снимков Для ГИС, предназначенной для решения различных научно-практических задач, важно использование информации,...
-
Постановка задачи - Анализ системы уравнений Сен-Венана аналитическими и численными методами
Важной задачей гидравлики открытых потоков является построение и изучение математической модели движения жидкости, которая позволяет осуществить расчет и...
-
В последнее время одним из главных направлений повышения качества проектирования, управления и контроля за разработкой нефтяных и газонефтяных...
-
В последнее время одним из главных направлений повышения качества проектирования, управления и контроля за разработкой нефтяных и газонефтяных...
-
Для работы с трехмерными моделями реальной местности, которые создаются в ГИС"Карта2011" применяется функция "Навигатор3D". "Навигатор3D" - это...
-
Загальна гідрологія - це комплексна наука про Землю, що фізико-математичними методами вивчає природні води разом з явищами та процесами, що в них...
-
Взаимодействие гравитационного и сейсмического полей Земли
Взаимодействие гравитационного и сейсмического полей Земли Под комплексной интерпретацией геофизических полей понимают такую процедуру совместного...
-
При кутових вимірюваннях основними джерелами помилок є: помилка центрування теодоліта, помилка редукції, помилка приладу, помилка за вплив довкілля,...
-
Геологія - Особливості Бразильського плоскогір'я
На значній частині нагір'я на поверхню виходять кристалічні породи древньої основи платформи. У його середній частині проходить смуга осадових...
-
Геологія та особливості складу рудоносних порід Вербинського рудопрояву молібдену
У статті розглянуто геолого-структурне положення Вербинського рудопрояву молібдену, розміщеного в північно-західній частині Волинського мегаблока...
-
Типовые трехмерные модели создаются по планам городов, топографическим картам или обзорным картам. Такие модели содержат в себе рельеф местности,...
-
Создание трехмерной модели - Объемное моделирование в геоинформационных системах
Для того, чтобы создать трехмерную модель - не нужна специальная подготовка, вполне хватит иметь матрицу высот и двухмерную карту. По таким исходным...
-
ВВЕДЕНИЕ, трехмерная модель местности - Объемное моделирование в геоинформационных системах
В связи со спросом на создание и реалистическим представлением пространственной информации происходит развитие и широкое распространение программных...
-
Трехмерные модели внутренних помещений создают используя поэтажные планы. С помощью трехмерных моделей внутренних помещений можно создать интерьер в...
-
Рослинний і тваринний світ, Грунтово-рослинний покрив - Особливості Бразильського плоскогір'я
Грунтово-рослинний покрив На Бразильському нагір'ї переважають савани і рідколистяні тропічні ліси. Відмінності в опадах в різних частинах області...
-
При спектральному аналізі було визначено 38 хімічних елементів у 20 зразках бурого вугілля різних макроскопічних типів. За даними спектрального аналізу...
-
Перші дослідження елементного складу та технічних характеристик для окремих родовищ, виконані та опубліковані В. М. Чирвінським (1938 р.). Комплексні...
-
У розділі представлені основні результати, отримані автором при інтерпретації та узагальнені матеріалів регіональних сейсмічних досліджень МВХ-СГТ,...
-
Геолого-экологические исследования и картографирование проводятся в разных масштабах. Мелкомасштабные исследования (1:1000000 - 1:500000) выполняются при...
-
Методи дослідження - Географічні особливості відтворення населення світу
Оскільки відтворення населення - явище демографічне, то і його рух можна досліджувати за допомогою безлічі методів, основні з яких можна об'єднати за їх...
-
Внедрение системного водоучета на действующих системах орошения предполагает режим эксплуатации каналов, при котором средства водоучета и управления...
-
Типи відтворення населення - Географічні особливості відтворення населення світу
Розглядаючи процес відтворення населення, можна виділити два основних типи. Перший тип відтворення населення - демографічна криза(синоніми: демографічна...
-
Метод модели прогрева дает возможность не только прогнозировать положение части осадочного разреза, находящейся в зоне ГФН, но и определять временной...
-
Взрывная подготовка горных пород Исходные данные: - Разрушаемые горные породы - Крепкие мергели; - Коэффициент крепости - 8-10; - Категория...
-
Використання теплових властивостей гірських порід для вирішення раціональних гірничотехнічних задач
Основний метод термічних досліджень масивів - вимір температур як по глибині так і площі. В географічних дослідженнях використовуються природні...
-
Седиментологическое обоснование модели резервуара - Методика разработки нефтегазового пласта АС11
Каротажный коллектор седиментологический литологический Создание геологической модели пласта-резервуара возможно лишь при достаточно детальных...
-
У розділі 1 наведено основні природні чинники формування хімічного складу поверхневих вод України. Річковий басейн разом із атмосферними опадами утворює...
-
Основные задачи геодезии как науки
Геодезия (греч. geфdaisнa, от gз -- Земля и dбiф -- делю, разделяю), наука об определении фигуры, размеров и гравитационного поля Земли и об измерениях...
-
Іридієва аномалія, Громова лисина, Дрейф нуля - Геологічні аномалії в світі
Ще однією природною аномалією вважається іридієва аномалія, розташована поблизу Рима. Геологічний шар, який за змістом іридію перевищує норму в 300...
-
Вугленосними в товщі осадових відкладів Дніпробасу є комплекси порід юрського, палеогенового та неогенового віку. Вугленосність юрського віку розвинена в...
-
Гідролого-кліматичні умови - Особливості Бразильського плоскогір'я
Кліматичні умови області різноманітні. Майже для всієї цієї величезної території характерно розподіл року на два періоди - вологий і сухий. Тривалість...
-
Задачи, виды и методы, технология исследования скважин и пластов - Основы добычи нефти и газа
Основная задача исследования залежей и скважин -- получение информации о них Для подсчета запасов нефти и газа, проектирования, анализа, регулирования...
-
Модель со степенным трендом - Роль и место природных ресурсов в мировой экономике
За независимую переменную примем t - год, за результирующую переменную примем у - объем мировой добычи природных ресурсов в стоимостном выражении (млрд....
-
Расчет прогнозной модели на перспективу 5 лет На первом этапе анализа на основе однофакторной линейной модели необходимо составить прогноз по объему...
Методологічні та програмно-алгоритмічні особливості розв'язання обернених задач - Прямі та обернені задачі гравіметрії в класі блочно побудованих геологічних моделей